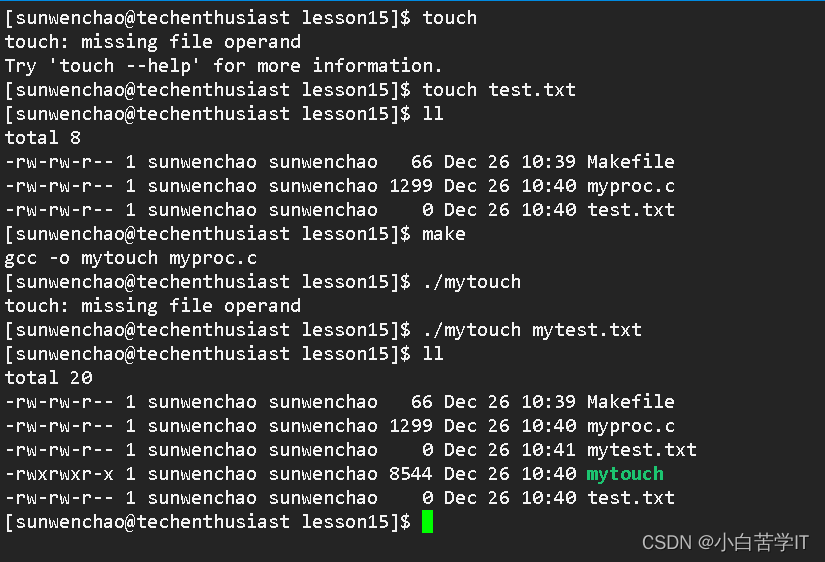
目录
- 1、itkIdentityTransform 一致变换
- 2、itkTranslationTransform 平移变换
- 3、itkScaleTransform 比例变换
- 4、itkRigid2DTransform 刚性2D变换
- 5、itkCenteredRigid2DTransform 居中刚性2D变换
- 6、itkEuler2DTransform 欧拉2D变换
- 7、itkSimilarity2DTransform 2D相似度变换
1、itkIdentityTransform 一致变换
该类的主要用途是调试,它定义身份转换的通用接口。
它将每个点映射到自身,每个向量映射到自身,每个协变向量映射到自身。
此类主要用作默认 Transform,用于初始化那些支持通用 Transform 的类。
此类是根据坐标表示类型(即用于表示点和向量分量的类型)和空间维度进行模板化的。 在这种情况下,输入和输出空间相同,因此只需要一维。
2、itkTranslationTransform 平移变换
该类实现向量空间的平移变换(例如空间坐标)。
平移变换的有点事计算快速并有很容易解释的参数。
使用仿射变换可以获得相同的功能,但性能差异很大。
Set/GetParameters():设置/获取用户指定的变换值的参数Set/GetOffset():设置/获取平移变换的偏移量,将 TranslationTransform 的偏移量设置为用户指定的值Set/GetIdentity():将参数设置/获取为 IdentityTransformGetNumberOfParameters():返回完整定义 Transform 的参数数量SetFixedParameters():设置固定参数并更新内部变换,Translation Transform 不需要固定参数,因此该方法的实现是空操作TransformPoint():通过仿射变换进行变换,该方法将自身给定的仿射变换应用于给定的点或向量,返回变换后的点或向量IsLinear():表明该变换是线性的,即给定两个点 P 和 Q,以及标量系数 a 和 b,则T(aP+bQ)=aT§+bT(Q)GetInverse():求仿射变换的逆,此方法创建并返回一个新的 TranslationTransform 对象,该对象是 self 的逆对象,如果 self 不可逆,则返回 falseGetInverseTransform():返回此变换的逆矩阵
typedef itk::TranslationTransform<double, Dimension> TransformType;
typename TransformType::Pointer transform = TransformType::New();
typename TransformType::ParametersType ParametersType ;
ParametersType initialParameters(transform->GetNumberOfParameters());
initialParameters[0] = 0.0; // Initial offset in mm along X
initialParameters[1] = 0.0; // Initial offset in mm along Y
transform->SetParameters(initialParameters);
3、itkScaleTransform 比例变换
该类实现向量空间的尺度变换(例如空间坐标)
它能沿着每一维度应用不同的缩放因数。点通过乘以沿着每一维度方向对应的缩放比例因数来实现坐标变换,
向量变换与点相同。协向量通过相应维的比例因子数区分他们成分的方法进行变换。
点: 变换后坐标 = 变换前坐标 * 每个维度变换系数
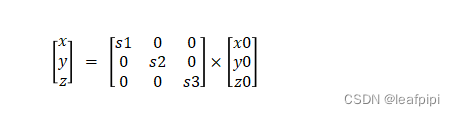
使用仿射变换可以获得相同的功能,但性能差异很大,因为仿射变换将使用对角矩阵的矩阵乘法。
Set/GetParameters():设置/获取参数,该方法设置用户指定的变换值的参数,参数的组织方式为scale[i] =parameter[i],在 3D 中,坐标 {x,y,z} 的比例参数分别为 {parameter[0],parameter[1],parameter[2]}SetScale():设置/获取缩放变换的因子,此方法无法使用 SetMacro 完成,因为 itk::Array 未定义运算符==,比例尺数组对应于要应用于每个坐标的因子,例如,在 3D 中,scale[0] 对应于 X,scale[1] 对应于 Y,scale[2] 对应于 ZSetIdentity():将转换设置为 Identity,这会将所有比例设置为 1.0Scale():将这个变换与另一个缩放组合起来。 pre 参数在这里无关紧要,因为尺度变换是可交换的,因此 pre 和 postcomposition 是等价的GetInverse():查找比例变换的逆,创建并返回一个新的 ScaleTransform 对象,该对象是 self 的逆,如果 self 不可逆,则返回 falseGetInverseTransform():返回此变换的逆矩阵
int Dimension = 3;
typedef itk::ScaleTransform<ScalarType, Dimension> ScaleTransformType;
typename ScaleTransformType::Pointer scaleTransform = ScaleTransformType::New();
ScaleTransformType::ParametersType scaleParameters(Dimension);
scaleParameters[0] = 0.6;
scaleParameters[1] = 0.7;
scaleParameters[2] = 0.8;
scaleTransform->SetParameters(scaleParameters);
itkScaleLogarithmicTransform和itkScaleTransform类似,唯一区别在于变换的参数是尺度的对数,有助于线性化用于优化的表达式。
4、itkRigid2DTransform 刚性2D变换
该类实现向量空间的刚性二维变换(例如空间坐标)。
此变换在 2D 空间中应用刚性变换, 变换被指定为围绕任意中心的旋转,然后是平移,在该类中,平移和旋转是独立的,且旋转使用弧度表示变换方程为:
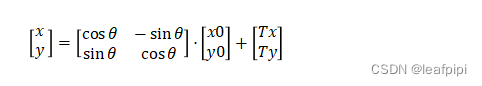
其中θ为自转角度,Tx和Ty是变换的成分。旋转以弧度制来进行测量,值在[-π,π]之间;平移使用mm测量。
可以使用单独的 Set 方法或使用 SetParameters() 和 SetFixedParameters() 以序列化形式设置此转换的参数。
可优化参数的序列化是一个由 3 个元素组成的数组,排序如下: p[0] = 角度, p[1] = 平移的 x 分量, p[2] = 平移的 y 分量。
固定参数的序列化是一个由 2 个元素组成的数组,排序如下: p[0] = 中心的 x 坐标, p[1] = 中心的 y 坐标。
中心、平移和底层矩阵偏移向量的访问方法记录在超类 MatrixOffsetTransformBase 中。
Set/GetAngle():设置/获取旋转角度(以弧度为单位)SetAngleInDegrees():设置旋转角度(以度为单位)SetIdentity():重置参数以创建和身份转换SetMatrix():设置 Rigid2D Transform 的旋转矩阵,此方法设置表示变换中旋转的 2x2 矩阵,矩阵应是正交的并具有一定的容差Set/GetParameters():设置/获取参数, 有3个参数, p[0] = 角度, p[1] = 平移的 x 分量, p[2] = 平移的 y 分量,旋转中心固定SetVarAngle():更新角度而不重新计算其他内部变量GetInverse():获取该变换的逆变换GetInverseTransform():返回此变换的逆矩阵
typedef itk::Rigid2DTransform<double> TransformType;
typename TransformType::Pointer transform = TransformType::New();
typename TransformType::TranslationType initialTranslation;
initialTranslation[0] = 5.0; //平移
initialTranslation[1] = 6.0;
typename TransformType::OutputPointType rotationCenter;
rotationCenter[0] = 100; //旋转中心
rotationCenter[1] = 100;
transform->SetIdentity();
transform->SetCenter(rotationCenter);
transform->SetAngle(1.0); //旋转角度
transform->SetTranslation(initialTranslation);
5、itkCenteredRigid2DTransform 居中刚性2D变换
该类实现向量空间的居中刚性二维变换(例如空间坐标)
与itkRigid2DTransform相似,该变换先围绕任意中心的旋转,然后是平移,主要区别在于,旋转中心可以任意选择进行优化。
可优化参数的序列化是一个由 5 个元素组成的数组,排序如下: p[0] = 角度, p[1] = 中心的 x 坐标, p[2] = 中心的 y 坐标, p[3] = 的 x 分量, 平移 p[4] = 平移的 y 分量。
没有固定的参数。
变换方程为:
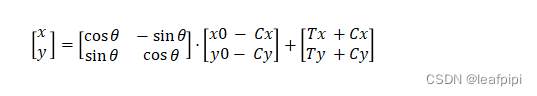
其中θ为自转角度,Cx和Cy为自转中心的坐标,它在自转前被减去在自转后增加恢复,Tx和Ty是变换的成分。旋转以弧度制来进行测量,值在[-π,π]之间;平移使用mm测量。
Set/GetParameters():设置/获取变换参数, 有5个参数, p[0] = 角度, p[1] = 中心的 x 坐标, p[2] = 中心的 y 坐标, p[3] = 的 x 分量, 平移 p[4] = 平移的 y 分量
其余函数继承自itkRigid2DTransform。
6、itkEuler2DTransform 欧拉2D变换
该类实现向量空间的欧拉二维变换(例如空间坐标)。
此变换应用 2D 空间的刚性变换,变换被指定为平面自转,然后二维平移。
继承自itkRigid2DTransform,与其功能相似。
typedef itk::Euler2DTransform<double> TransformType;
typename TransformType::Pointer transform = TransformType::New();
transform->SetAngle(0.0);//获取参数、矩阵等
typename TransformType::ParametersType parameters = transform->GetParameters();
typename TransformType::MatrixType matrix = transform->GetMatrix();
typename TransformType::OffsetType offset = transform->GetOffset();
7、itkSimilarity2DTransform 2D相似度变换
该类实现向量空间的相似度2D变换(例如空间坐标)
该变换在 2D 空间中应用均匀尺度和刚性变换,变换被指定为围绕任意中心的缩放和旋转,然后是平移, 给定一个旋转角度、均匀比例和平移 2D 偏移,变换公式为:
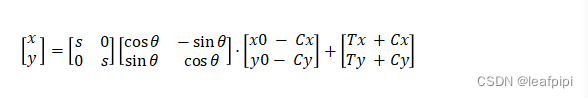
其中θ为自转角度,Cx和Cy为自转中心的坐标,它在自转前被减去在自转后增加恢复,Tx和Ty是变换的成分,s为缩放的比例因数。
可以使用单独的 Set 方法或使用 SetParameters() 和 SetFixedParameters() 以序列化形式设置此转换的参数。
可优化参数的序列化是一个由4个元素组成的数组,排序如下: p[0] = 比例, p[1] = 角度, p[2] = 平移的 x 分量, p[3] = 平移的 y 分量。
固定参数的序列化是一个由 2 个元素组成的数组,排序如下: p[0] = 中心的 x 坐标, p[1] = 中心的 y 坐标。
中心、平移和底层矩阵偏移向量的访问方法记录在超类 MatrixOffsetTransformBase 中。
角度的访问方法记录在超类 itkRigid2DTransform 中。
SetScale():设置/获取变换的缩放比例因数SetVarScale():设置比例而不更新基础变量Set/GetParameters():设置/获取变换参数, 有4个参数, p[0] = 比例, p[1] = 角度, p[2] = 平移的 x 分量, p[3] = 平移的 y 分量, 旋转中心固定
其余函数继承自itkRigid2DTransform。
typedef itk::Similarity2DTransform<double> TransformType;
typename TransformType::Pointer transform = TransformType::New();
typename TransformType::InputPointType rotationCenter;
rotationCenter[0] = 5.0;
rotationCenter[1] = 3.0;
typename TransformType::OutputVectorType translation;
translation[0] = 13.0;
translation[1] = 17.0;transform->SetAngle(angle); //旋转角度,弧度单位
transform->SetScale(scale); //缩放因子
transform->SetCenter(rotationCenter); //旋转中心
transform->SetTranslation(translation); //平移参数