模式识别与机器学习-判别式分类器
- 生成式模型和判别式模型的区别
- 线性判别函数
- 多分类情况
- 多分类情况1
- 多分类情况2
- 多分类情况3
- 例题
- 广义线性判别函数
- 实例
- 分段线性判别函数
- Fisher线性判别
- 感知机算法
- 例:
- 感知机多类别分类
谨以此博客作为学习期间的记录
生成式模型和判别式模型的区别
生成式模型关注如何生成整个数据的分布,而判别式模型则专注于学习如何根据给定输入预测输出标签或数值。在实践中多数判别式模型要优于生成式模型。

线性判别函数
对于一个两类问题来说,就是如何找到一条线(高维空间中是超平面)去将两类不同的样本分割开来。
若x是二维模式样本 x = [ x 1 x 2 ] T x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}^T x=[x1x2]T,其中 x 1 x_1 x1 和 x 2 x_2 x2是其坐标分量。
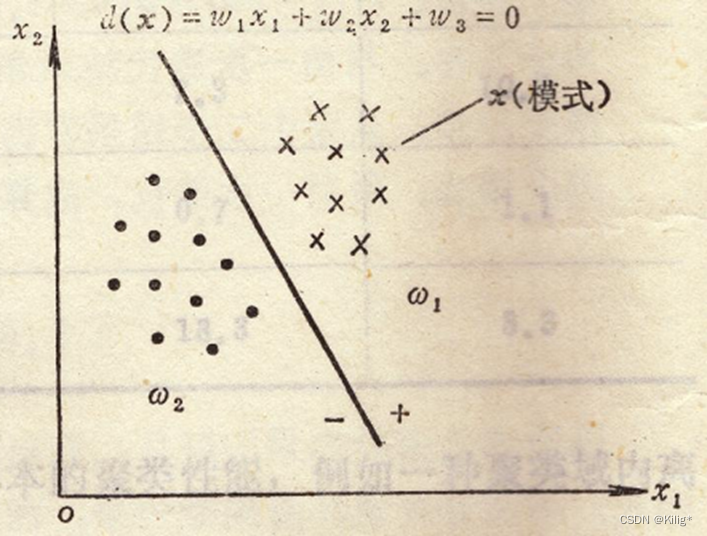
d ( x ) = w 1 x 1 + w 2 x 2 + w 3 = 0 d(x) = w_1x_1 + w_2x_2 + w_3 = 0 d(x)=w1x1+w2x2+w3=0
其中, x 1 x_1 x1、 x 2 x_2 x2为坐标变量, w 1 w_1 w1、 w 2 w_2 w2、 w 3 w_3 w3为参数方程。当一个未知类别的模式代入 d ( x ) d(x) d(x) 时:
- 若 d ( x ) > 0 d(x) > 0 d(x)>0,则 样本属于 w 1 w_1 w1
- 若 d ( x ) < 0 d(x) < 0 d(x)<0,则 样本属于 w 2 w_2 w2
此时, d ( x ) = 0 d(x) = 0 d(x)=0 称为判别函数。
n维线性判别函数的一般形式可以表示为: d ( x ) = w T x + w 0 = 0 d(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + w_0 = 0 d(x)=wTx+w0=0
其中, x = [ x 1 , x 2 , … , x n ] T \mathbf{x} = [x_1, x_2, \dots, x_n]^T x=[x1,x2,…,xn]T 表示 n 维模式样本, w = [ w 1 , w 2 , … , w n ] T \mathbf{w} = [w_1, w_2, \dots, w_n]^T w=[w1,w2,…,wn]T 是权重向量, w 0 w_0 w0 是偏置项或阈值。通过这个判别函数,可以将样本空间分割成不同的类别区域。
多分类情况
在二分类问题中,只需要根据判别函数 d ( x ) d(x) d(x)的正负即可将样本划分为不同的类别。但是在多分类问题中,情况较为复杂,有以下三种处理方式:
多分类情况1
用线性判别函数将属于 ω i ω_i ωi类的模式与不属于 ω i ω_i ωi类的模式分开,用多个判别函数来完成分类任务,每一个判别函数 d i ( x ) d_i(x) di(x)只有一个任务,那就是这个样本是否属于 w i w_i wi类。
判别情况通常可以表示为:
- 若 d i ( x ) > 0 d_i(x) > 0 di(x)>0,则样本 x x x 被判定为属于 ω i ω_i ωi 类。
- 若 d i ( x ) < 0 d_i(x) < 0 di(x)<0,则样本 x x x 被判定为不属于 ω i ω_i ωi 类。
多分类情况2
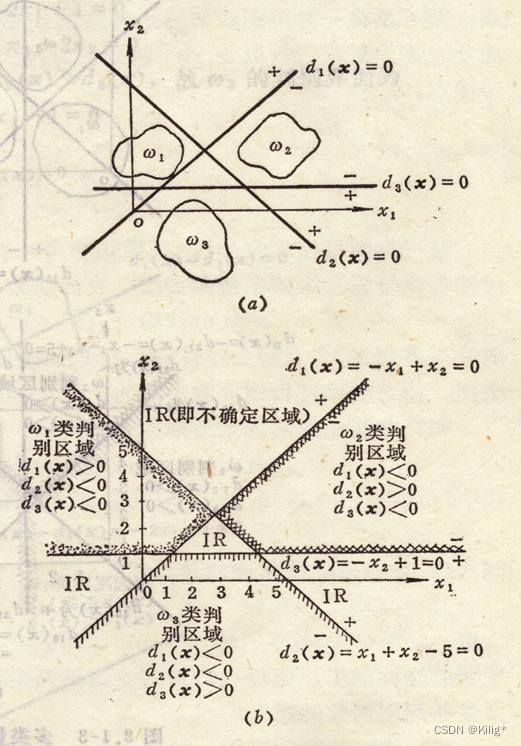
用多个判别函数来完成分类任务,判别函数 d i j ( x ) d_{ij}(x) dij(x)会判断样本x属于 w i w_i wi还是 w j w_j wj.
对一个三类情况, d 12 ( x ) = 0 对一个三类情况,d_{12}(x)=0 对一个三类情况,d12(x)=0仅能分开 ω 1 ω_1 ω1和 ω 2 ω_2 ω2类,不能分开 ω 1 ω_1 ω1和 ω 3 ω_3 ω3类。
要分开 M M M类模式,共需 M ( M − 1 ) 2 \frac{M(M-1)}{2} 2M(M−1)个判别函数。
不确定区域:若所有 d i j ( x ) d_{ij}(x) dij(x),找不到 d i j ( x ) > 0 d_{ij}(x)>0 dij(x)>0的情况。
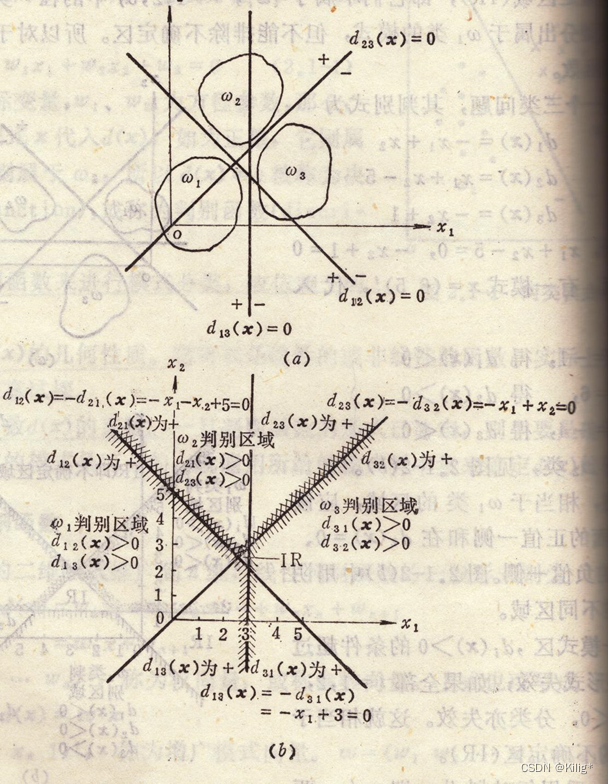
多分类情况3
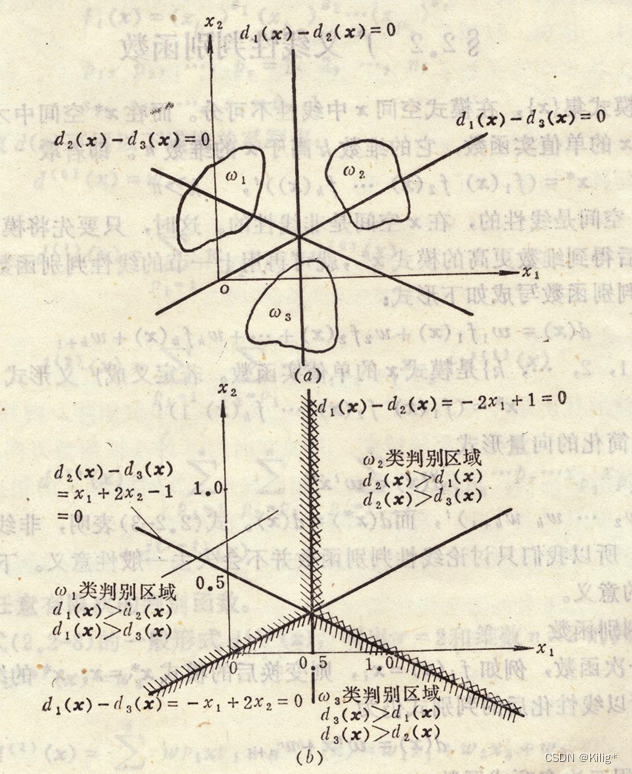
在这种情况下,判别函数可以分解 d i j ( x ) = d i ( x ) − d j ( x ) d_{ij}(x) = d_i(x) - d_j(x) dij(x)=di(x)−dj(x),其实 d i ( x ) d_i(x) di(x)可以理解为样本x距离类别 w i w_i wi的相似度,哪个 d i ( x ) d_i(x) di(x)大,x就离哪个类别近。

例题
Q1:
一个 10 类的模式识别问题中,有 3 类单独满足多类情况 1,其余的类别满足多类情况 2。问该模式识别问题所需判别函数的最少数目是多少?
A1:
将其余的类别满足多类情况 2的暂时先看为一类,这样的话需要4个判别函数就可以将 w 1 , w 2 , w 3 , { w 4 , w 5 , w 6 , w 7 , w 8 , w 9 , w 10 } w1,w2,w3,\{w4,w5,w6,w7,w8,w9,w10\} w1,w2,w3,{w4,w5,w6,w7,w8,w9,w10}划分开来,而要想将 w 4 , w 5 , w 6 , w 7 , w 8 , w 9 , w 10 w4,w5,w6,w7,w8,w9,w10 w4,w5,w6,w7,w8,w9,w10划分开,需要 7 ∗ ( 7 − 1 ) 2 = 21 \frac{7*(7-1)}{2} = 21 27∗(7−1)=21,因此一共需要21+4 = 25个判别函数。
Q2:
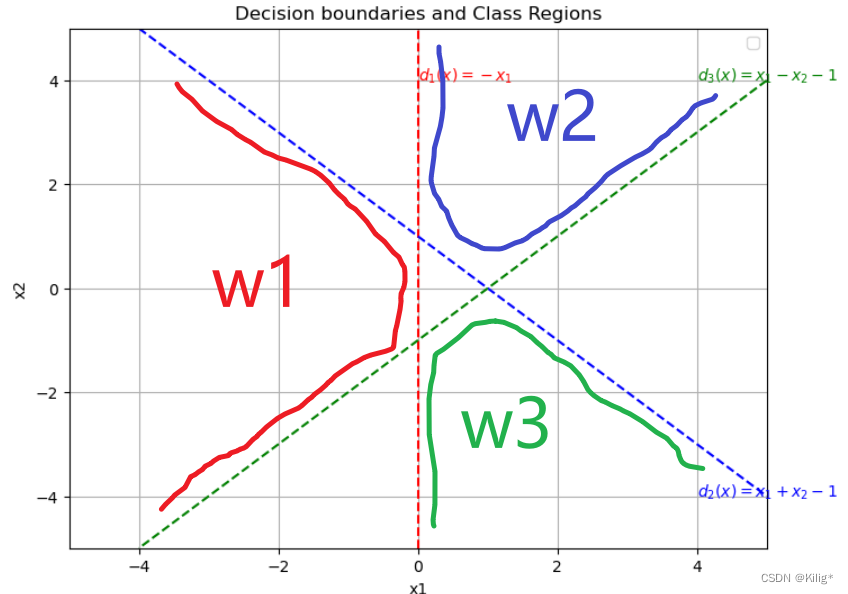
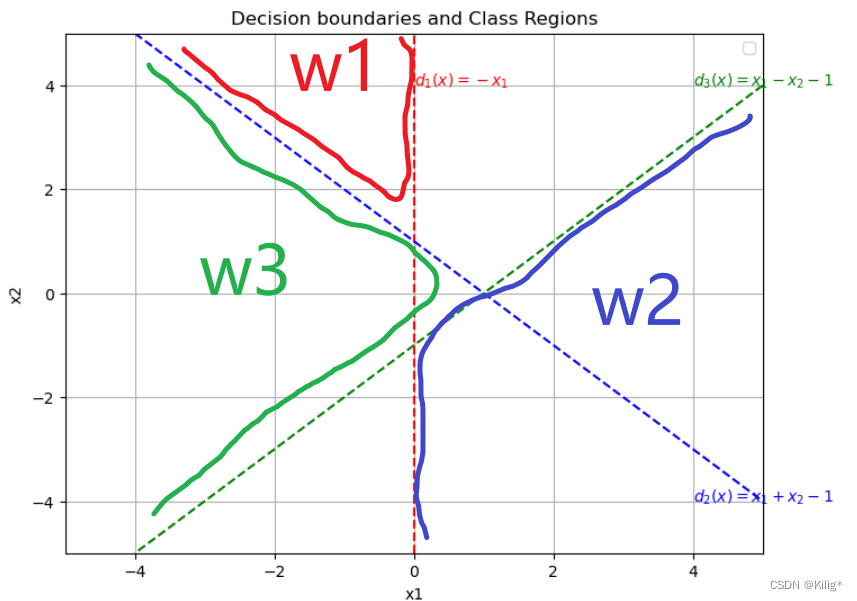
一个三类问题,其判别函数如下: d 1 ( x ) = − x 1 , d 2 ( x ) = x 1 + x 2 − 1 , d 3 ( x ) = x 1 − x 2 − 1 d_1(x) = -x_1,d_2(x) = x_1+x_2-1,d_3(x) = x_1-x_2-1 d1(x)=−x1,d2(x)=x1+x2−1,d3(x)=x1−x2−1
-
设这些函数是在多类情况 1 条件下确定的,绘出其判别界面和每一个模式类别的区域
-
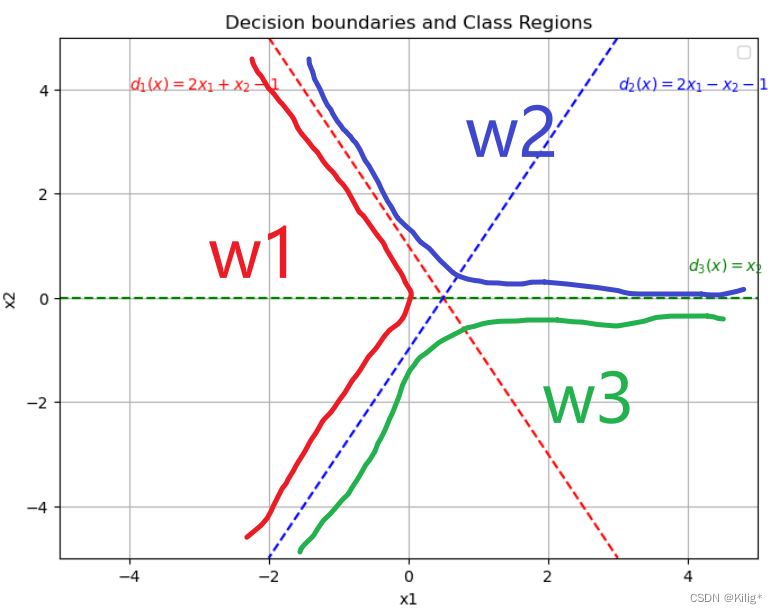
设为多类情况 2,并使: d 12 ( x ) = d 1 ( x ) , d 13 ( x ) = d 2 ( x ) , d 23 ( x ) = d 3 ( x ) d_{12}(x)= d_1(x), d_{13}(x)= d_2(x), d_{23}(x)= d_3(x) d12(x)=d1(x),d13(x)=d2(x),d23(x)=d3(x)。绘出其判别界面和多类情况 2 的区域
-
设 d 1 ( x ) , d 2 ( x ) 和 d 3 ( x ) d_1(x), d_2(x)和 d_3(x) d1(x),d2(x)和d3(x)是在多类情况 3 的条件下确定的,绘出其判别界面和每类的区域。
如果属于类别 w 1 w_1 w1,那么 d 1 ( x ) d_1(x) d1(x)是三个判别函数中最大的,有 − x 1 > x 1 + x 2 − 1 − x 1 > x 1 − x 2 − 1 -x_1 > x_1+x_2 - 1\\ -x_1>x_1-x_2-1 −x1>x1+x2−1−x1>x1−x2−1
化简之后有:
2 x 1 + x 2 − 1 < 0 2 x 1 − x 2 − 1 < 0 2x_1+x_2 - 1<0\\ 2x_1-x_2 - 1<0\\ 2x1+x2−1<02x1−x2−1<0
同理:
如果属于类别 w 2 w_2 w2,那么 d 2 ( x ) d_2(x) d2(x)是三个判别函数中最大的,有 x 1 + x 2 − 1 > − x 1 x 1 + x 2 − 1 > x 1 − x 2 − 1 x_1+x_2 - 1>-x_1\\ x_1+x_2 - 1>x_1-x_2-1 x1+x2−1>−x1x1+x2−1>x1−x2−1
化简之后有:
2 x 1 + x 2 − 1 > 0 x 2 > 0 2x_1+x_2 - 1>0\\ x_2>0\\ 2x1+x2−1>0x2>0
同理:
如果属于类别 w 3 w_3 w3,那么 d 3 ( x ) d_3(x) d3(x)是三个判别函数中最大的,有 x 1 − x 2 − 1 > − x 1 x 1 − x 2 − 1 > x 1 + x 2 − 1 x_1-x_2 - 1>-x_1\\ x_1-x_2 - 1>x_1+x_2-1 x1−x2−1>−x1x1−x2−1>x1+x2−1
化简之后有:
2 x 1 − x 2 − 1 > 0 x 2 < 0 2x_1-x_2 - 1>0\\ x_2<0\\ 2x1−x2−1>0x2<0
广义线性判别函数
基本思想:可以在线性判别函数的基础上添加一些非线性特征,从而具有更好的表达能力。
若有一个训练用的模式集 { x } \{x\} {x},在模式空间 x x x 中线性不可分,但在模式空间 x ∗ x^* x∗ 中线性可分。其中 x ∗ x^* x∗ 的各个分量是 x x x 的单值实函数, x ∗ x^* x∗ 的维数 k k k 高于 x x x 的维数 n n n,即若取
x ∗ = ( f 1 ( x ) , f 2 ( x ) , … , f k ( x ) ) , k > n x^* = (f_1(x), f_2(x), \dots, f_k(x)), \quad k > n x∗=(f1(x),f2(x),…,fk(x)),k>n
则分类界面在 x ∗ x^* x∗ 中是线性的,在 x x x 中是非线性的。此时只要将模式 x x x 进行非线性变换,使之变换后得到维数更高的模式 x ∗ x^* x∗,就可以用线性判别函数来进行分类。
此时广义线性判别函数可以表达为:
d ( x ) = w 1 f 1 ( x ) + w 2 f 2 ( x ) + . . . + w k f k ( x ) + w k + 1 d(x) = w_1f_1(x)+w_2f_2(x)+...+w_kf_k(x)+w_{k+1} d(x)=w1f1(x)+w2f2(x)+...+wkfk(x)+wk+1
实例
f i ( x ) f_i(x) fi(x)是 r r r次多项式, x x x是n维的情况。

Q3:
两类模式,每类包括 5 个 3 维不同的模式向量,且良好分布。如果它们是线性可分的,问权向量至少需要几个系数分量?假如要建立二次的多项式判别函数,又至少需要几个系数分量?(设模式的良好分布不因模式变化而改变。)
系数分量的个数为: C n + r r C_{n+r}^{r} Cn+rr
如果线性可分: C 4 1 = 4 C_{4}^{1} = 4 C41=4
如果建立二次判别函数: C 3 + 2 2 = 10 C_{3+2}^{2} = 10 C3+22=10
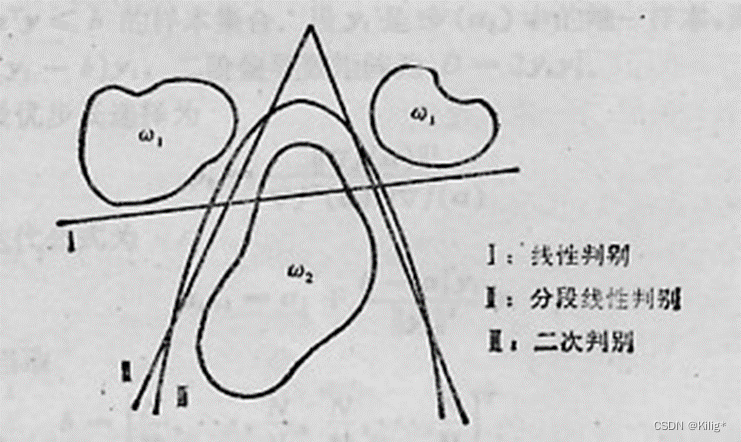
分段线性判别函数
在有些非线性可分场景下,可以使用二次判别函数,另一种处理方式是使用分段线性函数去逼近这个二次函数。
Fisher线性判别
在低维空间里解析上或计算上行得通的方法,在高维空间里往往行不通。因此,降低维数有时就会成为处理实际问题的关键。
思想:根据实际情况找到一条最好的、最易于分类的投影线。将点投影到这条线上实现降维。
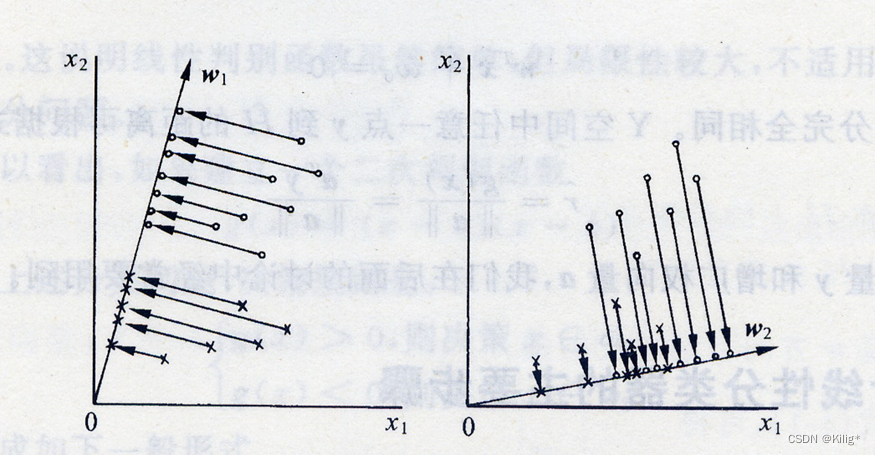
y n = W T x n y_n = W^Tx_n yn=WTxn这样就实现了从n维样本到一维的变换。关键在于如何确定W,从而使类内样本间隔尽可能小,类间样本间隔尽可能大。

最终求解得到的最优参数 w ∗ = S w − 1 ( m 1 − m 2 ) w*=S_w^{-1} (m_1-m_2) w∗=Sw−1(m1−m2)
感知机算法
感知器算法实质上是一种赏罚过程
- 对正确分类的模式则“赏”,实际上是“不罚”,即权向量不变。
- 对错误分类的模式则“罚”,使w(k)加上一个正比于 x k x_k xk的分量。
- 当用全部模式样本训练过一轮以后,只要有一个模式是判别错误的,则需要进行下一轮迭代,即用全部模式样本再训练一次。
- 如此不断反复直到全部模式样本进行训练都能得到正确的分类结果为止。

例:
- 用感知器算法求下列模式分类的解向量 w w w :
ω 1 : { ( 0 0 0 ) T , ( 1 0 0 ) T , ( 1 0 1 ) T , ( 1 1 0 ) T } ω 2 : { ( 0 0 1 ) T , ( 0 1 1 ) T , ( 0 1 0 ) T , ( 1 1 1 ) T } \begin{aligned} & \omega_1:\left\{\left(\begin{array}{lll} 0 & 0 & 0 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 1 & 0 & 0 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 1 & 0 & 1 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 1 & 1 & 0 \end{array}\right)^{\mathrm{T}}\right\} \\ & \omega_2:\left\{\left(\begin{array}{lll} 0 & 0 & 1 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 0 & 1 & 1 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 0 & 1 & 0 \end{array}\right)^{\mathrm{T}},\left(\begin{array}{lll} 1 & 1 & 1 \end{array}\right)^{\mathrm{T}}\right\} \\ & \end{aligned} ω1:{(000)T,(100)T,(101)T,(110)T}ω2:{(001)T,(011)T,(010)T,(111)T}
先将样本点写为增广形式
w 1 : { ( 0 , 0 , 0 , 1 ) , ( 1 , 0 , 0 , 1 ) , ( 1 , 0 , 1 , 1 ) , ( 1 , 1 , 0 , 1 ) } w 2 : { ( 0 , 0 , 1 , 1 ) , ( 0 , 1 , 1 , 1 ) , ( 0 , 1 , 0 , 1 ) , ( 1 , 1 , 1 , 1 ) } w_1:\{(0,0,0,1),(1,0,0,1),(1,0,1,1),(1,1,0,1)\}\\ w_2:\{(0,0,1,1),(0,1,1,1),(0,1,0,1),(1,1,1,1)\} w1:{(0,0,0,1),(1,0,0,1),(1,0,1,1),(1,1,0,1)}w2:{(0,0,1,1),(0,1,1,1),(0,1,0,1),(1,1,1,1)}
将属于 w 2 w_2 w2的样本统一乘上-1,得到 w 2 : { ( 0 , 0 , − 1 , − 1 ) , ( 0 , − 1 , − 1 , − 1 ) , ( 0 , − 1 , 0 , − 1 ) , ( − 1 , − 1 − 1 , − 1 ) } w_2:\{(0,0,-1,-1),(0,-1,-1,-1),(0,-1,0,-1),(-1,-1-1,-1)\} w2:{(0,0,−1,−1),(0,−1,−1,−1),(0,−1,0,−1),(−1,−1−1,−1)}
初始化 w 0 = ( 0 , 0 , 0 , 0 ) , C = 1 w_0 = (0,0,0,0),C = 1 w0=(0,0,0,0),C=1
w 0 ∗ ( 0 , 0 , 0 , 1 ) = 0 , w 1 = w 0 + C ∗ ( 0 , 0 , 0 , 1 ) = ( 0 , 0 , 0 , 1 ) w 1 ∗ ( 1 , 0 , 0 , 1 ) = 1 , w 2 = w 1 = ( 0 , 0 , 0 , 1 ) w 2 ∗ ( 1 , 0 , 1 , 1 ) = 1 , w 3 = w 2 = ( 0 , 0 , 0 , 1 ) w 3 ∗ ( 1 , 1 , 0 , 1 ) = 1 , w 4 = w 3 = ( 0 , 0 , 0 , 1 ) w 4 ∗ ( 0 , 0 , − 1 , − 1 ) = − 1 , w 5 = w 4 + C ∗ ( 0 , 0 , − 1 , − 1 ) = ( 0 , 0 , − 1 , 0 ) w 5 ∗ ( 0 , − 1 , − 1 , − 1 ) = 1 , w 6 = w 5 = ( 0 , 0 , − 1 , 0 ) w 6 ∗ ( 0 , − 1 , 0 , − 1 ) = 0 , w 7 = w 6 + C ∗ ( 0 , − 1 , 0 , − 1 ) = ( 0 , − 1 , − 1 , − 1 ) w 7 ∗ ( − 1 , − 1 , − 1 , − 1 ) = 3 , w 8 = w 7 = ( 0 , − 1 , − 1 , − 1 ) . . . w 39 = ( 2. , − 2. , − 2. , 1 ) d = 2 x 1 − 2 x 2 − 2 x 3 + x 4 w_0 * (0,0,0,1) = 0,\qquad w_1 = w_0 + C*(0,0,0,1) = (0,0,0,1)\\ w_1*(1,0,0,1) = 1,\qquad w_2 = w_1 = (0,0,0,1)\\ w_2*(1,0,1,1) = 1,\qquad w_3 = w_2 = (0,0,0,1)\\ w_3*(1,1,0,1) = 1,\qquad w_4 = w_3 = (0,0,0,1)\\ w_4*(0,0,-1,-1) = -1,\qquad w_5 = w_4 + C*(0,0,-1,-1) = (0,0,-1,0)\\ w_5*(0,-1,-1,-1) = 1,\qquad w_6 = w_5 = (0,0,-1,0)\\ w_6*(0,-1,0,-1) = 0,\qquad w_7 = w_6+C*(0,-1,0,-1) = (0,-1,-1,-1)\\ w_7*(-1,-1,-1,-1) = 3,\qquad w_8 = w_7 = (0,-1,-1,-1)\\ ...\\ w_{39} = (2., -2., -2., 1)\\ d = 2x_1-2x_2-2x_3+x_4 w0∗(0,0,0,1)=0,w1=w0+C∗(0,0,0,1)=(0,0,0,1)w1∗(1,0,0,1)=1,w2=w1=(0,0,0,1)w2∗(1,0,1,1)=1,w3=w2=(0,0,0,1)w3∗(1,1,0,1)=1,w4=w3=(0,0,0,1)w4∗(0,0,−1,−1)=−1,w5=w4+C∗(0,0,−1,−1)=(0,0,−1,0)w5∗(0,−1,−1,−1)=1,w6=w5=(0,0,−1,0)w6∗(0,−1,0,−1)=0,w7=w6+C∗(0,−1,0,−1)=(0,−1,−1,−1)w7∗(−1,−1,−1,−1)=3,w8=w7=(0,−1,−1,−1)...w39=(2.,−2.,−2.,1)d=2x1−2x2−2x3+x4
- 编写求解上述问题的感知器算法程序 (选做)
import numpy as np# 定义样本集
w1_samples = np.array([[0, 0, 0, 1], [1, 0, 0, 1], [1, 0, 1, 1], [1, 1, 0, 1]])
w2_samples = np.array([[0, 0, -1, -1], [0, -1, -1, -1], [0, -1, 0, -1], [-1, -1, -1, -1]])# 合并样本并初始化增广形式
X = np.vstack((w1_samples, w2_samples))# 初始权重向量和参数设置
w = np.zeros(X.shape[1]) # 初始权重向量
C = 1 # 正则化参数
converged = False # 收敛标志# 迭代更新权重向量
iteration = 0
while not converged:converged = Truefor i in range(X.shape[0]):if np.dot(w, X[i]) <= 0: # 判断误分类点w = w + C * X[i] # 更新权重向量converged = False # 存在误分类点,未收敛print(f"Iteration {iteration + 1}: w = {w}")iteration += 1print(f"\nConverged at iteration {iteration}: Final w = {w}")
输出结果:
Iteration 1: w = [0. 0. 0. 1.]
Iteration 2: w = [0. 0. 0. 1.]
Iteration 3: w = [0. 0. 0. 1.]
Iteration 4: w = [0. 0. 0. 1.]
Iteration 5: w = [ 0. 0. -1. 0.]
Iteration 6: w = [ 0. 0. -1. 0.]
Iteration 7: w = [ 0. -1. -1. -1.]
Iteration 8: w = [ 0. -1. -1. -1.]
Iteration 9: w = [ 0. -1. -1. 0.]
Iteration 10: w = [ 1. -1. -1. 1.]
Iteration 11: w = [ 1. -1. -1. 1.]
Iteration 12: w = [ 1. -1. -1. 1.]
Iteration 13: w = [ 1. -1. -2. 0.]
Iteration 14: w = [ 1. -1. -2. 0.]
Iteration 15: w = [ 1. -1. -2. 0.]
Iteration 16: w = [ 1. -1. -2. 0.]
Iteration 17: w = [ 1. -1. -2. 1.]
Iteration 18: w = [ 1. -1. -2. 1.]
Iteration 19: w = [ 2. -1. -1. 2.]
Iteration 20: w = [ 2. -1. -1. 2.]
Iteration 21: w = [ 2. -1. -2. 1.]
Iteration 22: w = [ 2. -1. -2. 1.]
Iteration 23: w = [ 2. -2. -2. 0.]
Iteration 24: w = [ 2. -2. -2. 0.]
Iteration 25: w = [ 2. -2. -2. 1.]
Iteration 26: w = [ 2. -2. -2. 1.]
Iteration 27: w = [ 2. -2. -2. 1.]
Iteration 28: w = [ 2. -2. -2. 1.]
Iteration 29: w = [ 2. -2. -2. 1.]
Iteration 30: w = [ 2. -2. -2. 1.]
Iteration 31: w = [ 2. -2. -2. 1.]
Iteration 32: w = [ 2. -2. -2. 1.]
Iteration 33: w = [ 2. -2. -2. 1.]
Iteration 34: w = [ 2. -2. -2. 1.]
Iteration 35: w = [ 2. -2. -2. 1.]
Iteration 36: w = [ 2. -2. -2. 1.]
Iteration 37: w = [ 2. -2. -2. 1.]
Iteration 38: w = [ 2. -2. -2. 1.]
Iteration 39: w = [ 2. -2. -2. 1.]
Iteration 40: w = [ 2. -2. -2. 1.]Converged at iteration 40: Final w = [ 2. -2. -2. 1.]
感知机多类别分类

用多类感知器算法求下列模式的判别函数:
ω 1 : ( − 1 , − 1 ) T , ω 2 : ( 0 , 0 ) T , ω 3 : ( 1 , 1 ) T ω_1: (-1, -1)^T, ω_2: (0, 0)^T, ω_3: (1, 1)^T ω1:(−1,−1)T,ω2:(0,0)T,ω3:(1,1)T
将样本写为增广形式 ω 1 : ( − 1 , − 1 , 1 ) T , ω 2 : ( 0 , 0 , 1 ) T , ω 3 : ( 1 , 1 , 1 ) T ω_1: (-1, -1,1)^T, ω_2: (0, 0,1)^T, ω_3: (1, 1,1)^T ω1:(−1,−1,1)T,ω2:(0,0,1)T,ω3:(1,1,1)T
初始化 d 1 ( x ) = ( 0 , 0 , 0 ) , d 2 ( x ) = ( 0 , 0 , 0 ) , d 3 ( x ) = ( 0 , 0 , 0 ) d_1(x) = (0,0,0),d_2(x) = (0,0,0),d_3(x) = (0,0,0) d1(x)=(0,0,0),d2(x)=(0,0,0),d3(x)=(0,0,0)
d 1 ∗ w 1 = 0 , d 2 ∗ w 1 = 0 , d 3 ∗ w 1 = 0 , d 1 = d 1 + w 1 = ( − 1 , − 1 , 1 ) , d 2 = d 2 − w 1 = ( 1 , 1 , − 1 ) , d 3 = d 3 − w 1 = ( 1 , 1 , − 1 ) d 1 ∗ w 2 = 1 , d 2 ∗ w 2 = − 1 , d 3 ∗ w 3 = − 1 , d 1 = d 1 − w 2 = ( − 1 , − 1 , 0 ) , d 2 = d 2 + w 2 = ( 1 , 1 , 0 ) , d 3 = d 3 − w 2 = ( 1 , 1 , − 2 ) d 1 ∗ w 3 = − 2 , d 2 ∗ w 3 = 2 , d 3 ∗ w 3 = 0 , d 1 = ( − 1 , − 1 , 0 ) , d 2 = d 2 − w 3 = ( 0 , 0 , − 1 ) , d 3 = d 3 + w 3 = ( 2 , 2 , − 1 ) d 1 ∗ w 1 = 2 , d 2 ∗ w 1 = − 1 , d 3 ∗ w 1 = − 5 , d 1 = ( − 1 , − 1 , 0 ) , d 2 = ( 0 , 0 , − 1 ) , d 3 = ( 2 , 2 , − 1 ) d 1 ∗ w 2 = 0 , d 2 ∗ w 2 = − 1 , d 3 ∗ w 2 = − 1 , d 1 = d 1 − w 2 = ( − 1 , − 1 , − 1 ) , d 2 = d 2 + w 2 = ( 0 , 0 , 0 ) , d 3 = d 3 − w 2 = ( 2 , 2 , − 2 ) d 1 ∗ w 3 = − 3 , d 2 ∗ w 3 = 0 , d 3 ∗ w 3 = 2 , d 1 = ( − 1 , − 1 , − 1 ) , d 2 = ( 0 , 0 , 0 ) , d 3 = ( 2 , 2 , − 2 ) d 1 ∗ w 1 = 1 , d 2 ∗ w 1 = 0 , d 3 ∗ w 1 = − 6 , d 1 = ( − 1 , − 1 , − 1 ) , d 2 = ( 0 , 0 , 0 ) , d 3 = ( 2 , 2 , − 2 ) d 1 ∗ w 2 = − 1 , d 2 ∗ w 2 = 0 , d 3 ∗ w 2 = − 2 , d 1 = ( − 1 , − 1 , − 1 ) , d 2 = ( 0 , 0 , 0 ) , d 3 = ( 2 , 2 , − 2 ) d_1*w_1 = 0,\quad d_2*w_1 = 0,\quad d_3*w_1 = 0,\quad d_1 = d_1 + w_1 = (-1,-1,1),\quad d_2 = d_2 - w_1 = (1,1,-1),\quad d_3 = d_3 - w_1 = (1,1,-1)\\ d_1*w_2 = 1,\quad d_2*w_2 = -1,\quad d_3*w_3 = -1,\quad d_1 = d_1 - w_2 = (-1,-1,0),\quad d_2 = d_2 + w_2 = (1,1,0),\quad d_3 = d_3 - w_2 = (1,1,-2)\\ d_1*w_3 = -2,\quad d_2*w_3 = 2,\quad d_3*w_3 = 0,\quad d_1 = (-1,-1,0),\quad d_2 = d_2 - w_3 = (0,0,-1),\quad d_3 = d_3 + w_3 = (2,2,-1)\\ d_1*w_1 = 2,\quad d_2*w_1 = -1,\quad d_3*w_1 = -5,\quad d_1 = (-1,-1,0),\quad d_2 = (0,0,-1),\quad d_3 = (2,2,-1)\\ d_1*w_2 = 0,\quad d_2*w_2 = -1,\quad d_3*w_2 = -1,\quad d_1 =d_1 - w_2 = (-1,-1,-1),\quad d_2 = d_2 + w_2 = (0,0,0),\quad d_3 =d_3 -w_2 = (2,2,-2)\\ d_1*w_3 = -3,\quad d_2*w_3 = 0,\quad d_3*w_3 = 2,\quad d_1 = (-1,-1,-1),\quad d_2 = (0,0,0),\quad d_3 = (2,2,-2)\\ d_1*w_1= 1,\quad d_2*w_1= 0,\quad d_3*w_1 = -6,\quad d_1 = (-1,-1,-1),\quad d_2 = (0,0,0),\quad d_3 = (2,2,-2)\\ d_1*w_2= -1,\quad d_2*w_2= 0,\quad d_3*w_2 = -2,\quad d_1 = (-1,-1,-1),\quad d_2 = (0,0,0),\quad d_3 = (2,2,-2)\\ d1∗w1=0,d2∗w1=0,d3∗w1=0,d1=d1+w1=(−1,−1,1),d2=d2−w1=(1,1,−1),d3=d3−w1=(1,1,−1)d1∗w2=1,d2∗w2=−1,d3∗w3=−1,d1=d1−w2=(−1,−1,0),d2=d2+w2=(1,1,0),d3=d3−w2=(1,1,−2)d1∗w3=−2,d2∗w3=2,d3∗w3=0,d1=(−1,−1,0),d2=d2−w3=(0,0,−1),d3=d3+w3=(2,2,−1)d1∗w1=2,d2∗w1=−1,d3∗w1=−5,d1=(−1,−1,0),d2=(0,0,−1),d3=(2,2,−1)d1∗w2=0,d2∗w2=−1,d3∗w2=−1,d1=d1−w2=(−1,−1,−1),d2=d2+w2=(0,0,0),d3=d3−w2=(2,2,−2)d1∗w3=−3,d2∗w3=0,d3∗w3=2,d1=(−1,−1,−1),d2=(0,0,0),d3=(2,2,−2)d1∗w1=1,d2∗w1=0,d3∗w1=−6,d1=(−1,−1,−1),d2=(0,0,0),d3=(2,2,−2)d1∗w2=−1,d2∗w2=0,d3∗w2=−2,d1=(−1,−1,−1),d2=(0,0,0),d3=(2,2,−2)
因此最终
d 1 = − x 1 − x 2 − 1 d 2 = 0 d 3 = 2 x 1 + 2 x 2 − 2 d_1 = -x_1 - x_2 - 1\\ d_2 = 0\\ d_3 = 2x_1+2x_2-2 d1=−x1−x2−1d2=0d3=2x1+2x2−2







![[Angular] 笔记 10:服务与依赖注入](https://img-blog.csdnimg.cn/direct/c5f4e7938b7a48cd999fdb21660c4127.png)