基本指令

grep

1. grep可以过滤文本行
done用于标记循环的结束，确保循环体在指定条件下正确执行，下图是一个打印的循环体的脚本

2. 把包含9的文本行过滤出来了

有三种写法,文本可以带双引号,单引号,或者都不带
root@hcss-ecs-93fe:~/hello# grep "9" log.txt
grep '9' log.txt
grep 9 log.txt

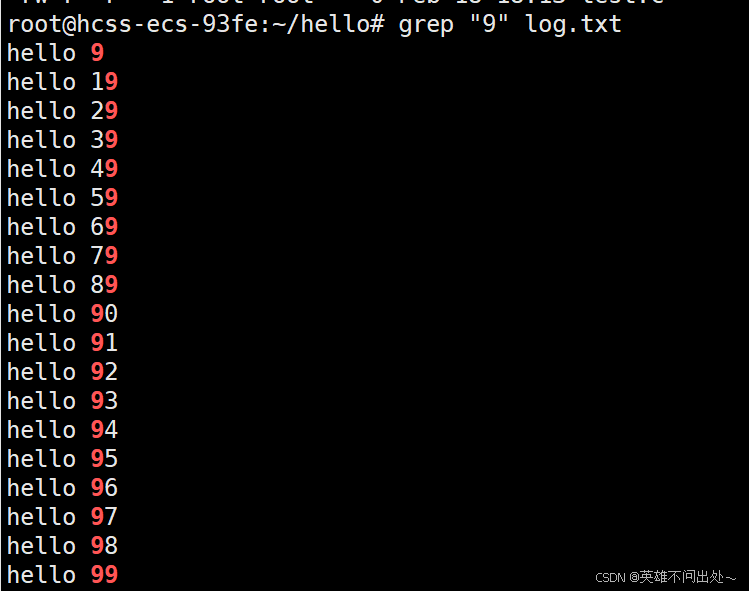
3. grep -n 可以显示行号，grep -v，逆向的，可以将除匹配成功的以外的文本保留下来

grep -n "9" log.txt
grep -v "9" log.txt
把除9之外的文本保留下来了

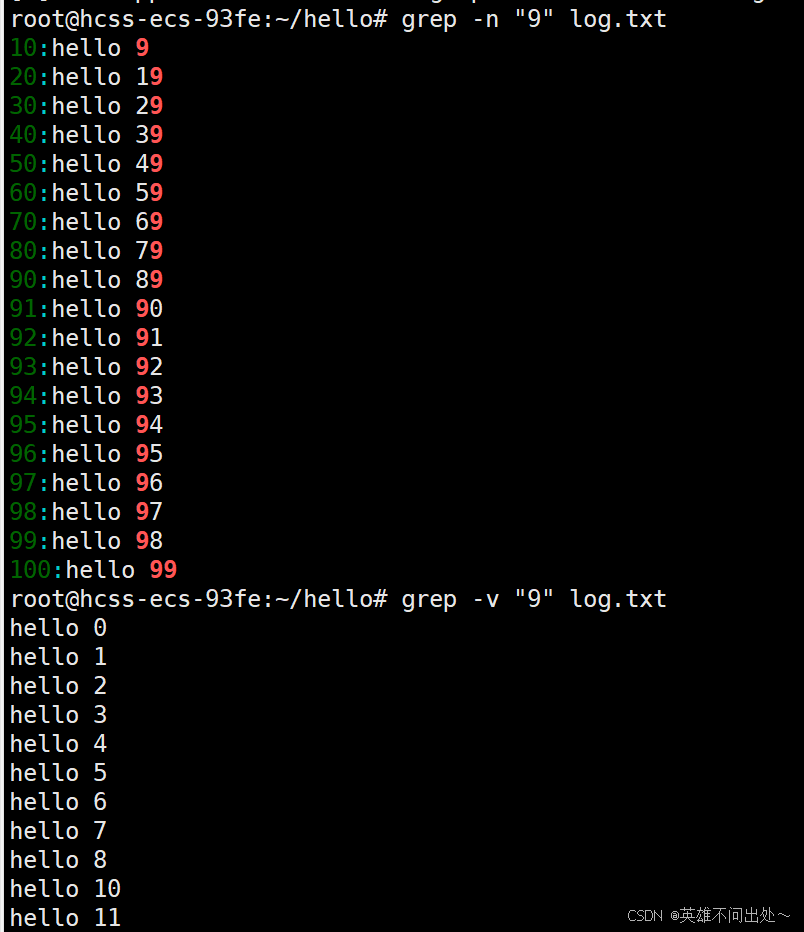
4. grep -i “hello” log.txt，-i选项可以忽略大小写匹配，ignore，也就是大小写都会打印到显示器上

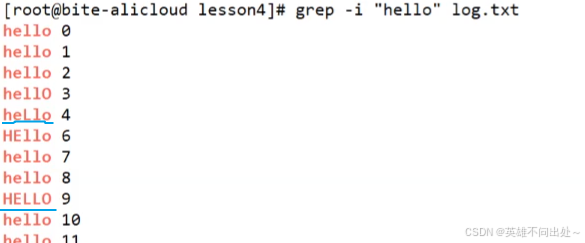
5. grep -v “hello” log.txt，把不匹配hello的选项显示出来

6. grep -vi “hello” log.txt，忽略大小写匹配，将匹配失败的显示出来

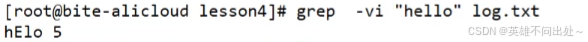
7. grep把所有的包含关键字"Removed"并且是从后往前找的10个信息打印出来

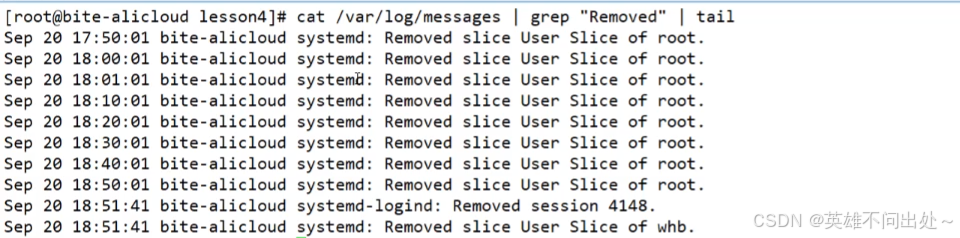
grep "Removed" var/log/messages | tail -10
grep "Removed" var/log/messages

8. ps ajx 可以查看历史进程
在进程中查找"muprocess"

9. * 匹配当前目录下的所有文件

grep -n "int main" *
在文本中查找指定的行 

打包和压缩

zip/unzip

检测zip有没有装上，version版本

// 安装zip和unzip
apt install -y zip unzip

1. 不带选项只能打包单个文件
2. 比如说目录只能打包这个空目录

zip lesson.zip lesson
// 将lesson打包成lesson.zip
unzip lesson.zip
// 将lesson解压解包到当前文件夹

3. 要打包目录要带上-r选项

zip -r lesson.zip lesson

4. 解压到指定的目录下需要-d选项

// 将lesson.zip解压到指定的/root目录下
unzip lesson.zip -d /root

Linux和windows压缩包互传

安装sz和rz命令
apt install -y lrzsz

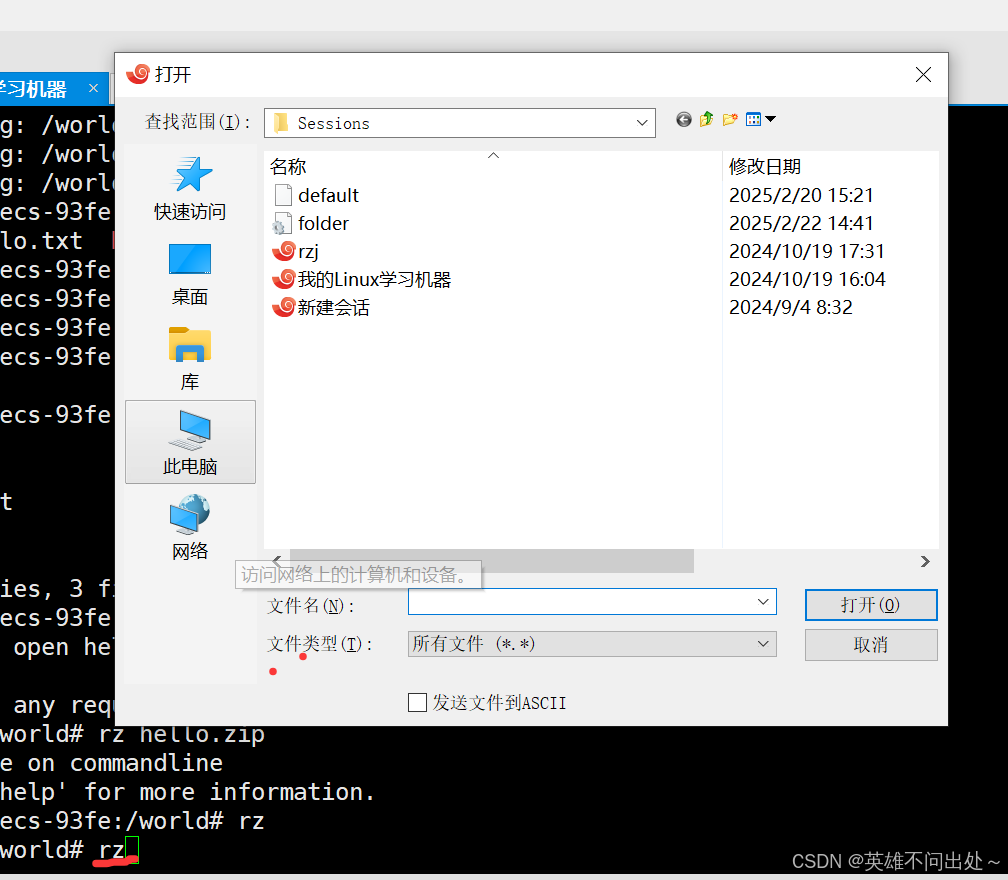
1. rz：用于远端设备发送文件到本地计算机（例如windows中的压缩包传到Linux中）
2. sz：用于从本地计算机发送文件到远端设备
（例如Linux中的压缩包传到windows中）

sz hello.zip
// 发送压缩包到windows中

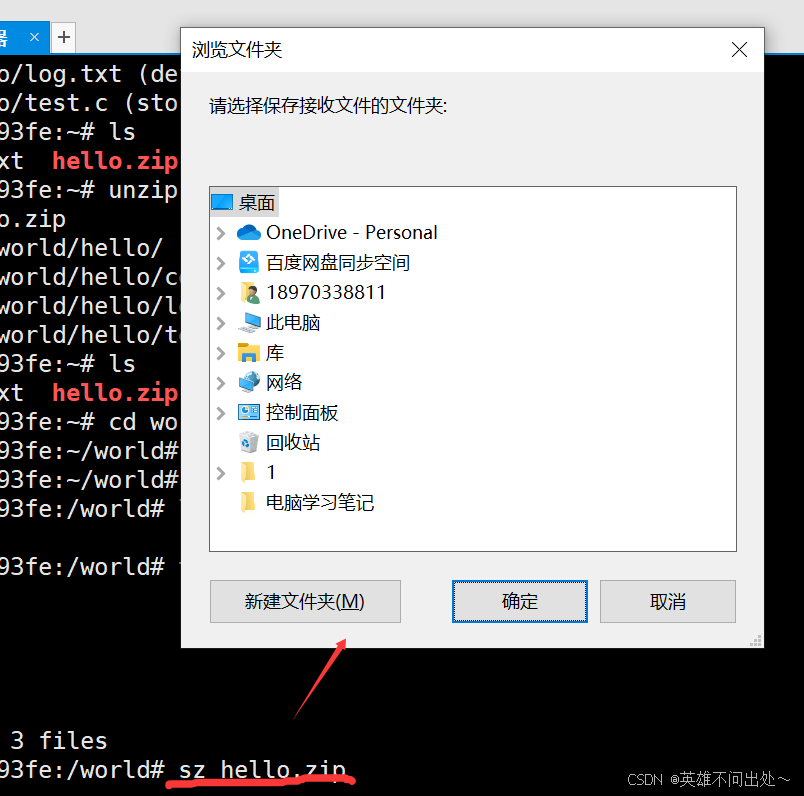
rz 
// 从windows中接收压缩包到Linux中

tar（重要）

// 将srcdir打包压缩为xxx.tgz的压缩包
tar 选项 xxx.tgz srcdir

1. 选项：c 新建一个打包文件
z 把打包文件进行压缩
f 指定文档名，使用档名，请留意，在 f 之后要立即接档名喔！不要再加参数！
x 解开一个压缩文件
2. tar命令默认是递归的

打包压缩文件
tar czf lesson.tgz lesson
解压压缩包
tar xzf lesson.tgz

3. -v选项可以展示解包/压缩的过程并且显示文件

4. 创建一万个普通文件

5. tar xzf lesson.tgz -C /root
将lesson.tgz解压到指定目录下

tar -xzf lesson.tgz -C /root
// 选项的前面可以带-也可以不带-

Linux和Linux压缩包互传

1. scp 远程拷贝的命令
2. 拷贝完之后，需要输入另一台Linux机器的密码，之后就可以在另一台机器上看到压缩包

bc

1. bc相当与Linux当中简单的计算器

作用：

uname -r

1. uname用来获取电脑和操作系统的相关信息
2. uname可显示linux主机所用的操作系统的版本、硬件的名称等基本信息
3. -a或‒all 详细输出所有信息，依次为内核名称，主机名，内核版本号，内核版本，硬件名，处理器类型，硬件平台类型，操作系统名称

• 怎么在Linux环境下查看你的体系结构和系统内核版本呢？

uname -r
体系结构是指一个系统的基本组织结构，包括其组件、组件之间的关系、组件与外部环境的关系，以及指导系统设计和演进的原则，例如x64，AMD
体系结构就是芯片结构

1. x86_32 x86_64(x64)
2. 新老内核的问题
   一般公司都会选择老内核，因为比较稳定

系统内核版本
内核版本号通常由四部分组成：主版本号.次版本号.修订版本号-补丁版本号
红色的为体系结构
蓝色的为内核版本

常用的热键

1. \ 是续行符，相当于 ls -a -l
2. 如果误触了\，想要马上回到新的命令行，ctrl+c终止当前程序
3. 上下键查看历史命令
4. tab键快速按两下，可以自动地进行命令搜索和命令补全

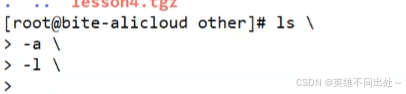
tab

5. ctrl + r搜索历史命令

6. ctrl + d 退出当前用户
7. history 显示历史命令，Linux会记录我们的历史命令

关机

1.一些关机的命令： shutdown 关机 halt 挂起 reboot 重启
2. 云服务器永不关机，除非维护了或者不用了

shutdown -h 立即关机
shutdown -h -t 秒数 
意味着多少秒关机

外壳程序

为什要存在外壳程序：

• 方便用户操作，用户不能直接访问操作系统，要用Shell作为中间商
• 如果用户输入了一个错误指令，外壳就把指令拦截了下来，相当于保护了内核

bash是Linux当中的外壳程序，bash在Linux中是一个死循环，shell是外壳程序的统称

• 总结

• 外壳程序是操作系统外部的一套软件

• 将使用者的命令翻译给核心（Linux）（kernel）处理

• 同时，将核心（Linux）的处理结果翻译给使用者

知识点

打包和压缩

• 什么是打包和压缩 ？

1. 打包：文件合并，将多个文件合并为一个文件
2.压缩：减少体积

• 为什么要打包和压缩 ？

1.打包：防止文件丢失
2. 压缩：减少体积，节省存储空间，可以有效地减少网络传送的时间

• 怎么打包和压缩 ？

1. 打包和压缩不做明显的区分，因为在Linux中打包和压缩分开看很麻烦

Linux中的权限

用户权限

1. Linux中的用户：root用户（超级用户）or 普通用户
2. windows：管理员（admin）or 普通用户
3. 超级用户：权限高 普通用户：权限低，受管控

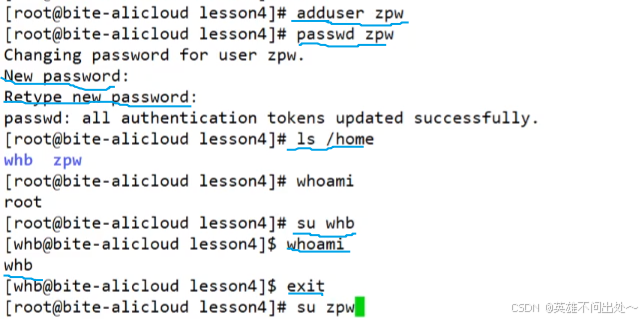
身份切换：普通用户编程超级用户，要输入超级用户的密码
su ->将普通用户转为超级用户

• exit / ctrl + d：都可以从超级用户回退到普通用户或者让普通用户回退到超级用户
• su：不会让用户重新登录，只是身份的切换，不会影响当前所处的目录，还是当前所处的路径
• su -：是让用户重新登录了，会让所处的路径发生变化

• who是当前有哪些人在登录
  

• 超级用户用命令回退到普通用户怎么做？
  1、su 用户名：可以不输密码，直接回退到指定的普通用户