力扣：62. 不同路径（动态规划，附python二维数组的定义）

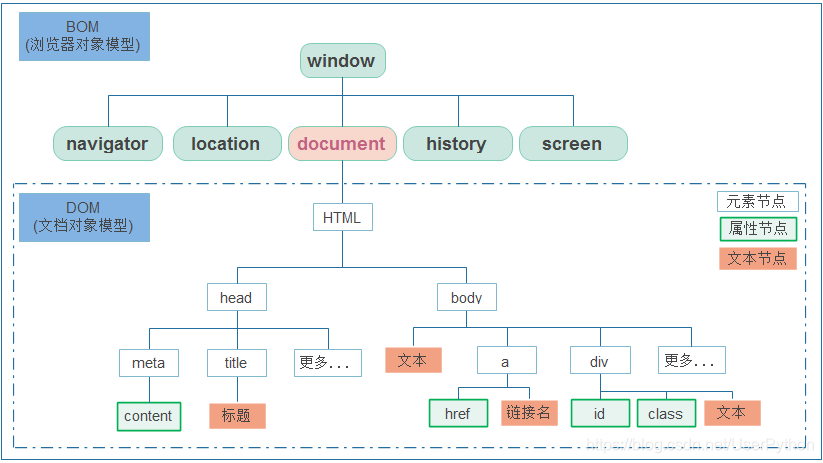
题目：

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

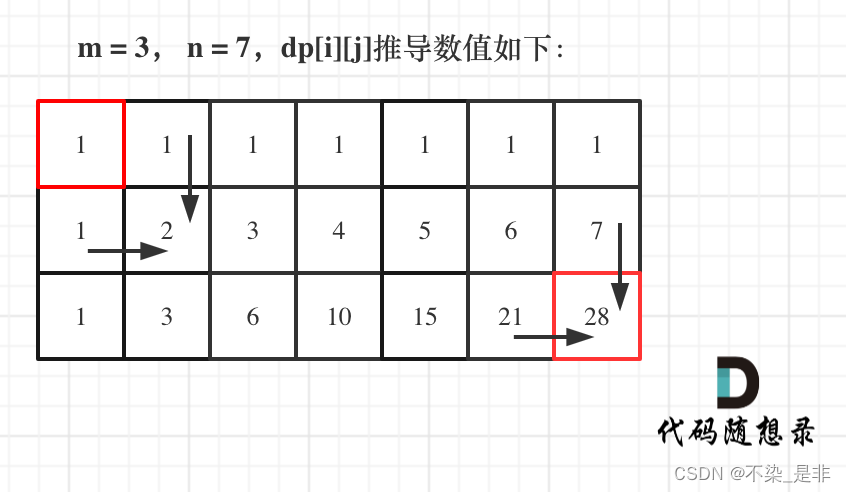
输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下
示例 3：

输入：m = 7, n = 3
输出：28
示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109

思路：

刚看到这道题第一时间想不到这跟动态规划有什么关系，这不是图的深搜吗？
但大家试过之后就会发图的深搜会超时。

动态规划：

机器人从(0 , 0) 位置出发，到(m - 1, n - 1)终点。

按照动规五部曲来分析：

确定dp数组，以及下标的含义

这里要明确dp数组的含义，定义dp数组是为了找到不同路径，
dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

确定递推公式

这道题的递归公式不像之前的题一下就能看出来，
想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]。

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理。

那么很自然，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来。

可能有人会疑惑 dp[i - 1][j] 向下走一步就到dp[i][j]，dp[i][j - 1]向右走一步就到dp[i][j]，那为什么dp[i][j] 不等于 dp[i - 1][j] + dp[i][j - 1] + 1 + 1 呢？这里要明白dp数组的含义，这里dp数组求的是路径而不是步数，你走一步路径数并没有发生变化。

dp数组的初始化

如何初始化呢，首先dp[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

确定遍历顺序

这里要看一下递推公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

这样就可以保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的。

举例推导dp数组

如图所示：

这里要说明一下dp数组的日志打印，如果你提交不通过，你可以直接输出dp数组，看看你是哪一步出现问题，然后对症下药。

定义二维数组

写过很多要定义二维数组的题了，但依然是一写就忘，这里稍微说一下python中二维数组的定义，

方法一：

dp = [[0] * n for _ in range(m)]

方法二（跟一其实是一个东西）：

dp = [[0 for i in range(n)] for j in range(m)]

方法三（NumPy库）：

import numpy as np# 创建一个n×m的二维数组，初始值为0  np.ones((n, m)) 初始值为1
array = np.zeros((n, m))

完整代码：

class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]