周期噪声
对于具有周期性的噪声被称为周期噪声,其中周期噪声在频率域会出现关于中心对称的性质,如下图所示

带阻滤波器
为了消除周期性噪声,由此设计了几种常见的滤波器,其中 W W W表示带阻滤波器的带宽
理想带阻滤波器
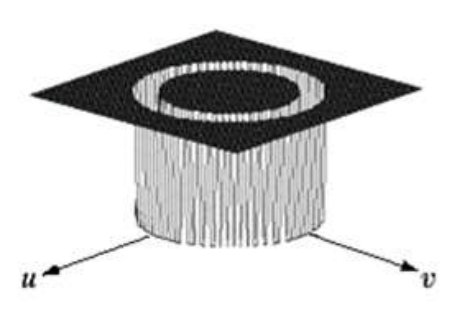
H ( u , v ) = { 1 D ( u , v ) < D 0 − W 2 0 D 0 − W 2 < D ( u , v ) < D 0 + W 2 1 D ( u , v ) > D 0 + W 2 H(u,v)=\begin{cases}1&&D(u,v)<D_0-\frac{W}{2}\\0&&D_0-\frac{W}{2}<D(u,v)<D_0+\frac{W}{2}\\1&&D(u,v)>D_0+\frac{W}{2}&\end{cases} H(u,v)=⎩ ⎨ ⎧101D(u,v)<D0−2WD0−2W<D(u,v)<D0+2WD(u,v)>D0+2W
巴特沃斯带阻滤波器
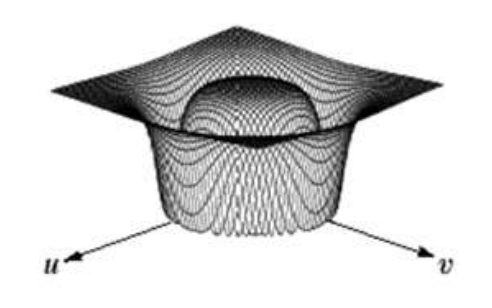
H ( u , v ) = 1 1 + [ D ( u , v ) W D 2 ( u , v ) − D 0 2 ] 2 n H(u,v)=\frac1{1+\left[\frac{D(u,v)W}{D^2(u,v)-D_0^2}\right]^{2n}} H(u,v)=1+[D2(u,v)−D02D(u,v)W]2n1
高斯带阻滤波器
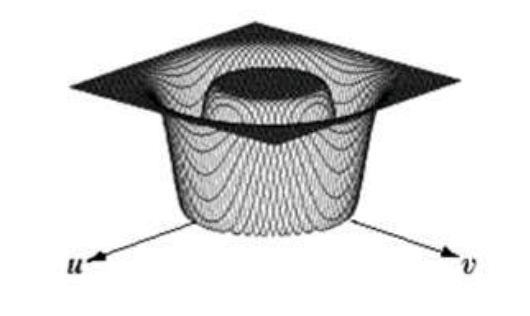
H ( u , v ) = 1 − exp [ − 1 2 ( D 2 ( u , v ) − D 0 2 D ( u , v ) W ) 2 ] H(u,v)=1-\exp[-\frac12(\frac{D^2(u,v)-D_0^2}{D(u,v)W})^2] H(u,v)=1−exp[−21(D(u,v)WD2(u,v)−D02)2]
带阻滤波器所对应的带通滤波器则为 1 − 带阻滤波器 1-\text{带阻滤波器} 1−带阻滤波器