本节介绍一个在神经网络中非常常见的激活函数 - Relu 激活函数。
什么是ReLU激活函数
ReLU 英文名为 Rectified Linear Unit,又称修正线性单元,是一种简单但很有效的激活函数,它的定义如下:

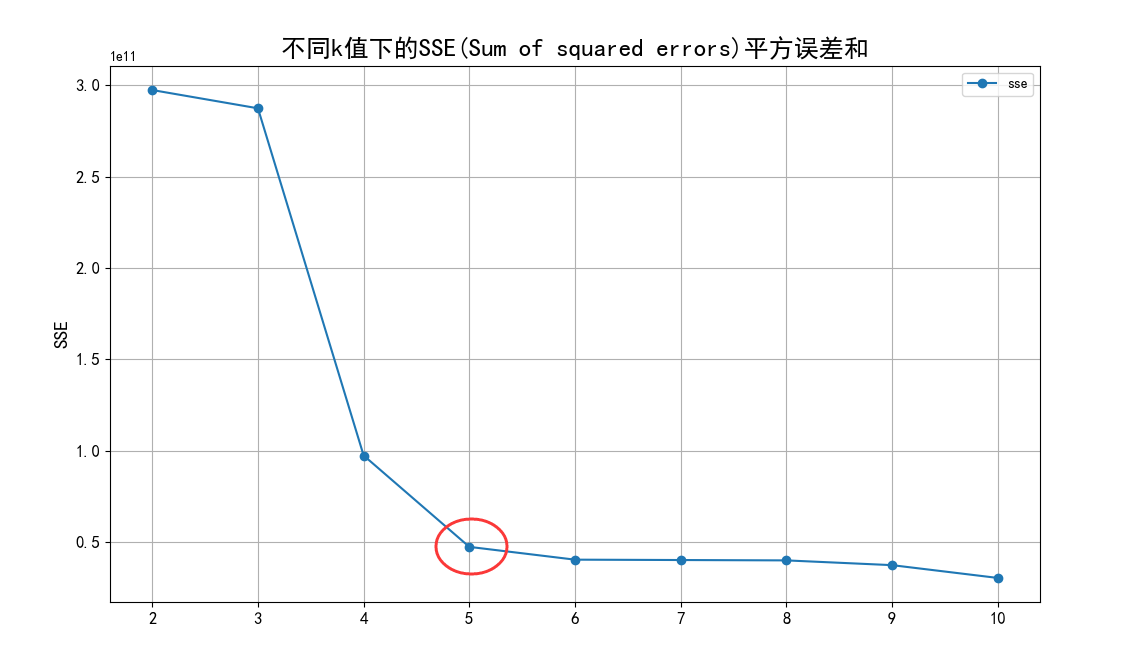
即当输入 x 大于零时,输出等于他自己;当输入小于等于零时,输出为零,下面是relu的图像表示。

看着是不是很简单,但是就是因为如此简单,才使得 Relu 激活在神经网络中非常常见。
为何ReLU激活函数如此常见?
ReLU之所以广泛应用,主要归功于以下几个方面:
-
ReLU引入了非线性因素
上节我们说了在神经网络中非线性因素是非常重要的,Relu 函数本身就是一个非线性函数,它大于零的部分是线性的,但是小于零的部分是零,从而整体上表现为一种非线性特性。