pandas库是Python数据分析的核心库 它不仅可以加载和转换数据，还可以做更多的事情：它还可以可视化 pandas绘图API简单易用，是pandas流行的重要原因之一
Pandas 单变量可视化
单变量可视化， 包括条形图、折线图、直方图、饼图等
数据使用葡萄酒评论数据集，来自葡萄酒爱好者杂志，包含10个字段，150929行，每一行代表一款葡萄酒
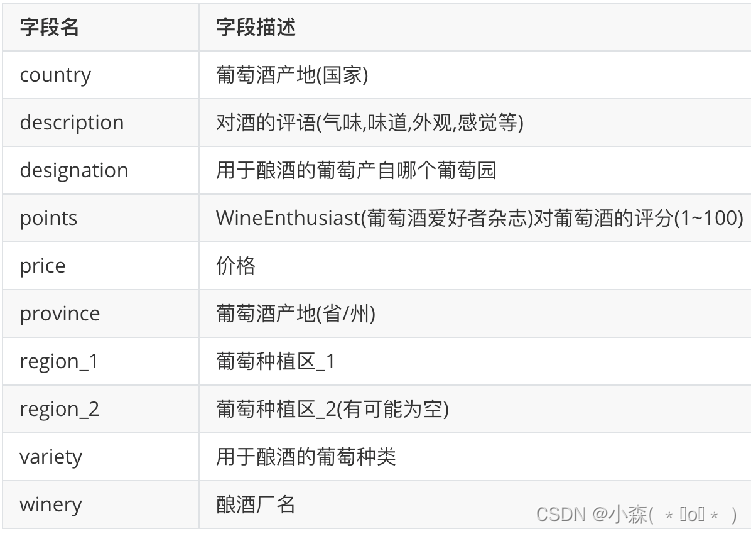
加载数据
条形图是最简单最常用的可视化图表 在下面的案例中，将所有的葡萄酒品牌按照产区分类，看看哪个产区的葡萄酒品种多：
先将plot需要的参数打包成一个字典，然后在使用**解包（防止传进去的成为一个参数）
上面的图表说明加利福尼亚生产的葡萄酒比其他省都多
也可以折算成比例, 计算加利福尼亚葡萄酒占总数的百分比 :
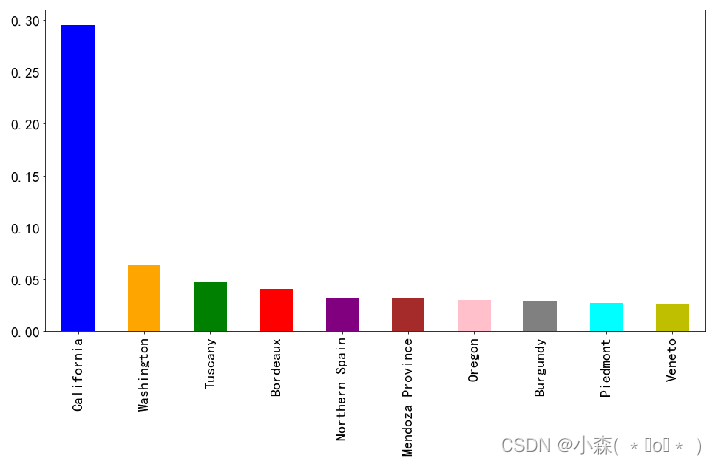
条形图(柱状图)非常灵活： 高度可以代表任何东西，只要它是数字即可 每个条形可以代表任何东西，只要它是一个类别即可。
也可以用来展示《葡萄酒杂志》（Wine Magazine）给出的评分数量的分布情况：
如果要绘制的数据不是类别值，而是连续值比较适合使用折线图 :
柱状图和折线图区别 柱状图：简单直观，很容易根据柱子的长短看出值的大小，易于比较各组数据之间的差别
折线图： 易于比较各组数据之间的差别； 能比较多组数据在同一个维度上的趋势； 每张图上不适合展示太多折线
面积图就是在折线图的基础上，把折线下面的面积填充颜色 ：
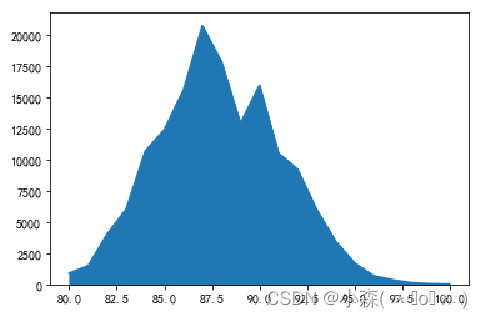
直方图
直方图看起来很像条形图， 直方图是一种特殊的条形图，它可以将数据分成均匀的间隔，并用条形图显示每个间隔中有多少行， 直方图柱子的宽度代表了分组的间距，柱状图柱子宽度没有意义
直方图缺点：将数据分成均匀的间隔区间，所以它们对歪斜的数据的处理不是很好： 
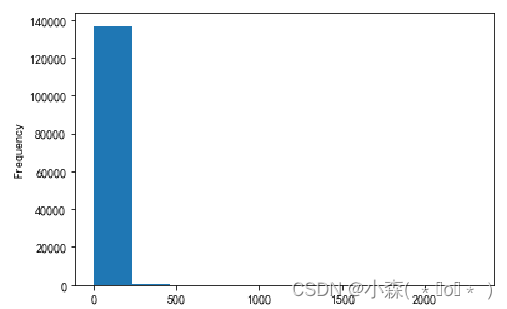
在第一个直方图中，将价格>200的葡萄酒排除了。
在第二个直方图中，没有对价格做任何处理，由于有个别品种的酒价格极高，导致刻度范围变大，导致直方图的价格分布发生变化 。
数据倾斜： 当数据在某个维度上分布不均匀，称为数据倾斜
- 一共15万条数据，价格高于1500的只有三条
- 价格高于500的只有73条数据，说明在价格这个维度上，数据的分布是不均匀的
- 直方图适合用来展示没有数据倾斜的数据分布情况，不适合展示数据倾斜的数据
饼图
饼图也是一种常见的可视化形式
reviews['province'].value_counts().head(10).plot.pie()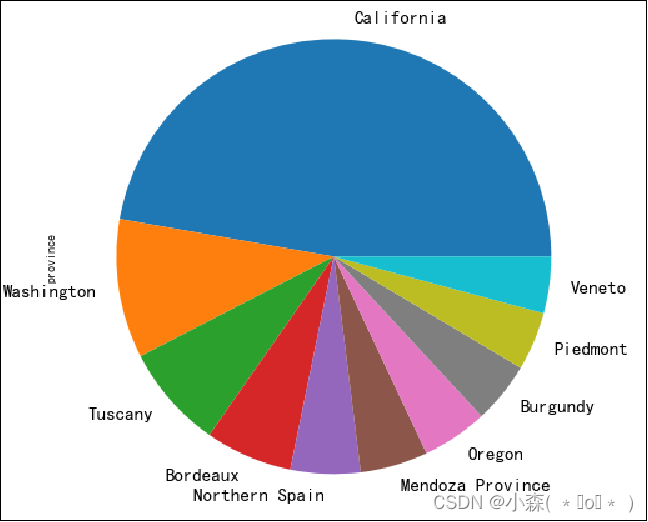
饼图的缺陷：饼图只适合展示少量分类在整体的占比
- 如果分类比较多，必然每个分类的面积会比较小，这个时候很难比较两个类别
- 如果两个类别在饼图中彼此不相邻，很难进行比较
- 可以使用柱状图图来替换饼图
Pandas 双变量可视化
数据分析时，我们需要找到变量之间的相互关系，比如一个变量的增加是否与另一个变量有关，数据可视化是找到两个变量的关系的最佳方法；
散点图
最简单的两个变量可视化图形是散点图，散点图中的一个点，可以表示两个变量
reviews[reviews['price'] < 100].sample(100).plot.scatter(x='price', y='points’)
调整图形大小，字体大小，由于pandas的绘图功能是对Matplotlib绘图功能的封装，所以很多参数pandas 和 matplotlib都一样
reviews[reviews['price'] < 100].sample(100).plot.scatter(x='price', y='points',figsize=(14,8),fontsize = 16)
修改x轴 y轴标签字体
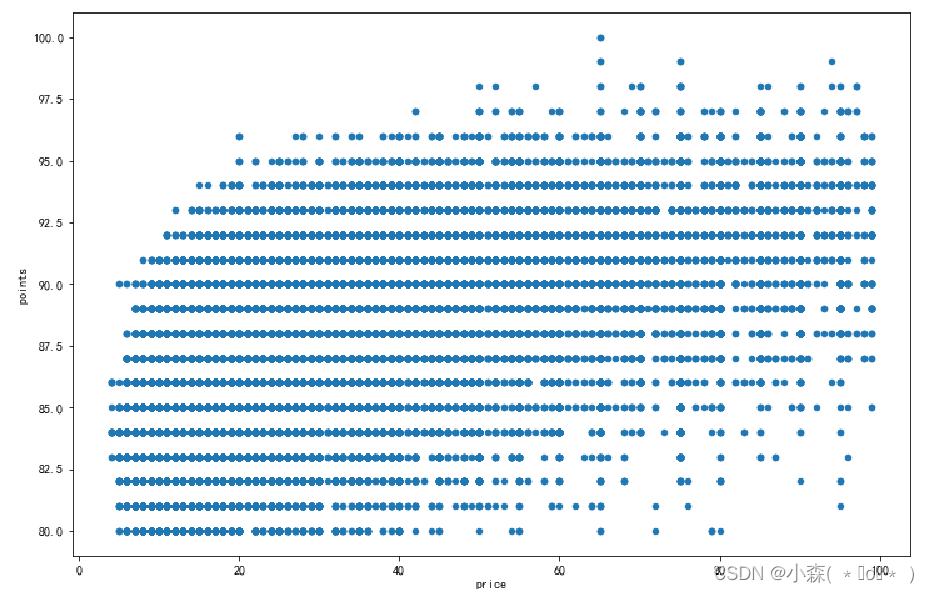
上图显示了价格和评分之间有一定的相关性：也就是说，价格较高的葡萄酒通常得分更高。
散点图最适合使用相对较小的数据集以及具有大量唯一值的变量。 有几种方法可以处理过度绘图。 一：对数据进行采样 二：hexplot(蜂巢图)
hexplot
hexplot将数据点聚合为六边形，然后根据其内的值为这些六边形上色：
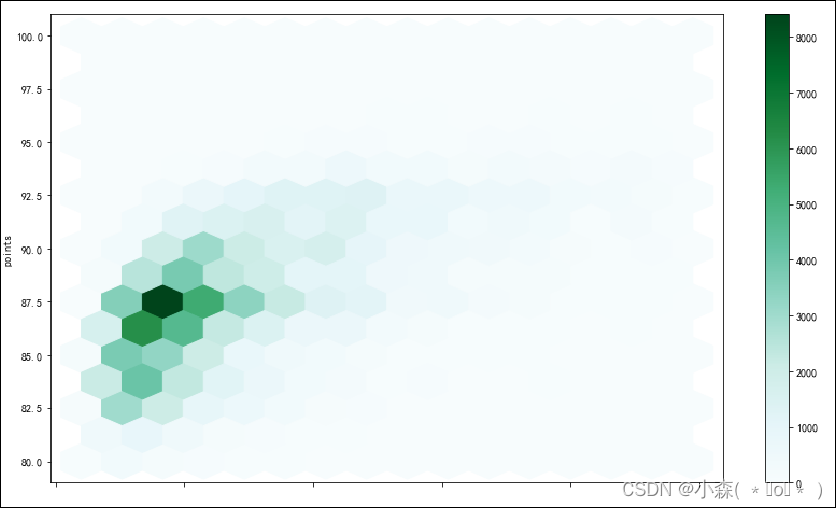
上图x轴坐标缺失，属于bug，可以通过调用matplotlib的api添加x坐标：
该图中的数据可以和散点图中的数据进行比较，但是hexplot能展示的信息更多
从hexplot中，可以看到《葡萄酒杂志》（Wine Magazine）评论的葡萄酒瓶大多数是87.5分，价格20美元 Hexplot和散点图可以应用于区间变量和/或有序分类变量的组合。
堆叠图（Stacked plots）
- 展示两个变量，除了使用散点图，也可以使用堆叠图
- 堆叠图是将一个变量绘制在另一个变量顶部的图表
- 接下来通过堆叠图来展示最常见的五种葡萄酒
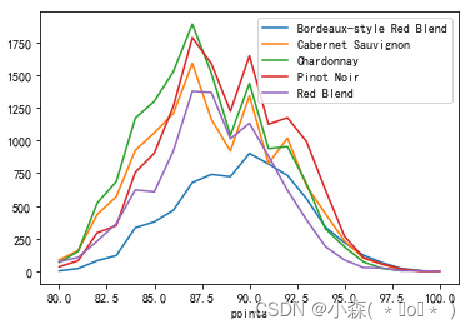
从结果中看出，最受欢迎的葡萄酒是，Chardonnay（霞多丽白葡萄酒），Pinot Noir（黑皮诺），Cabernet Sauvignon（赤霞珠），Red Blend（混酿红葡萄酒） ，Bordeaux-style Red Blend （波尔多风格混合红酒）
从数据中取出最常见的五种葡萄酒：
通过透视表找到每种葡萄酒中，不同评分的数量 ：
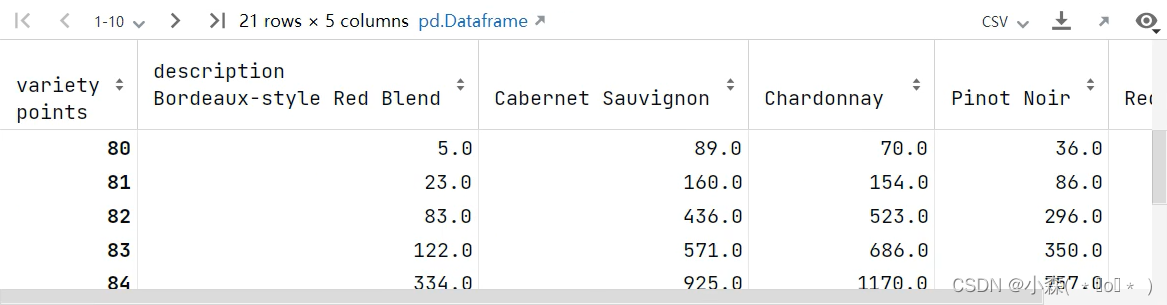
从上面的数据中看出，行列分别表示一个类别变量（评分，葡萄酒类别），行列交叉点表示计数，这类数据很适合用堆叠图展示
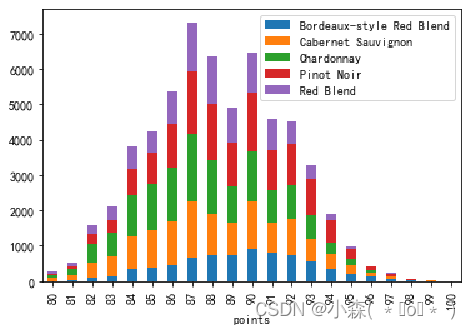
折线图在双变量可视化时，仍然非常有效
wine_counts.plot.line()
