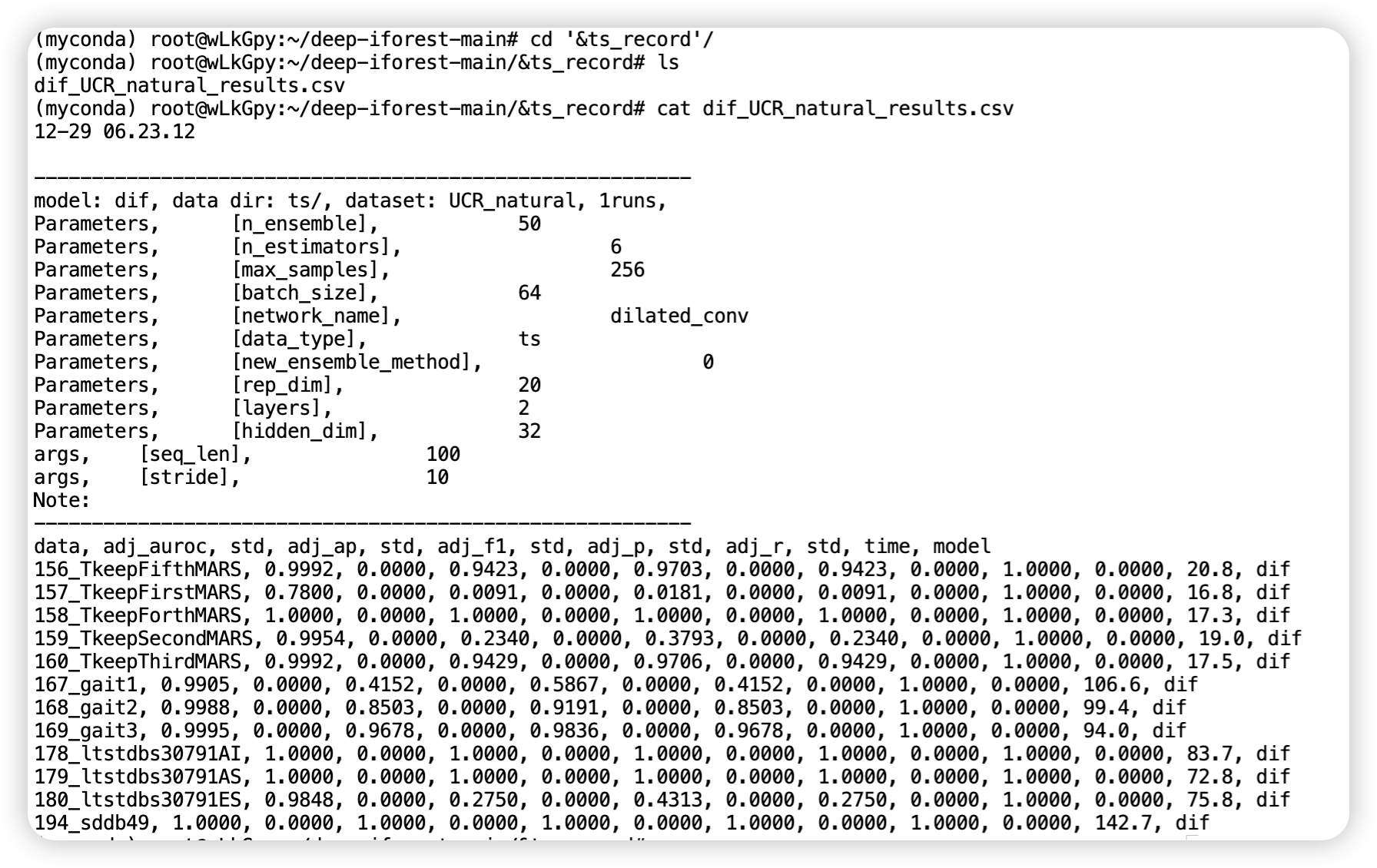
题目:
给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角 。沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和 * 返回累加和最小值
思路:
1. 既然是给定二维数组matrix,那么二维数组的数据是知道的
2. 这个人只能从左上角出发,目的地是右下角
3. 沿途只能向下或者向右走。那么第一行和第一列的值是可以知道的。
假设这个二维数组是:
| 3 | 7 | 9 | 6 |
| 6 | 5 | 3 | 9 |
| 8 | 3 | 1 | 5 |
| 4 | 7 | 9 | 2 |
根据这个二维数组推导:
第一行的数据只能往右走,因为它不存在上方数据,依此可以推导出:
| 3 | 10 | 19 | 25 |
第一列的数据,只能往下走,因为它不存在左边的数据,以此可以推导
| 3 | 10(3+7) | 19(10+9) | 25(19+6) |
| 9(3+6) | |||
| 17(9+8) | |||
| 21(17+4) |
已经推导出第一行和第一列的数据,接下来开始推导剩下的数据。因为每一个格子的数据都是依赖上一行的当前列或者当前行的前一列的值。谁小,就要谁。以此可以推导出:
| 3 | 10 | 19 | 25 |
| 9 | 14(9<10取 9+5) | 17(14<19 取14+3) | 26(17<25 取17+9) |
| 17 | 17(14<17 取14+3) | 18 | 23(18<26 取 18+5) |
| 21 | 24 (17<21 取 17+7) | 27 (18<24 取 18+9) | 25 (23<27 取 23+2) |
推导公式已经出来了。下面看代码的实现:
public static int minSum (int[][] matrix){if (matrix == null || matrix.length == 0) {return 0;}//行数int row = matrix.length;//列数int col = matrix[0].length;//如果是100*100规模的二维数组。那么dp的空间开销巨大int[][] dp = new int[row][col];//dp的第一行值只能依赖左边的值dp[0][0] = matrix[0][0];//构建dp表的第一行数据for (int colIndex = 1; colIndex < col; colIndex++) {//前一列和当前列的累加和,放入dp表dp[0][colIndex] = dp[0][colIndex -1] + matrix[0][colIndex];}//构建dp表的第一列数据for (int rowIndex = 1; rowIndex < row; rowIndex++) {//上一列和当前列的累加和,放入dp表dp[rowIndex][0] = dp[rowIndex -1][0] + matrix[rowIndex][0];}for (int rowIndex = 1; rowIndex < row; rowIndex++) {for (int colIndex = 1; colIndex < col; colIndex++) {//先获取上一行当前列 与 当前行的前一列 较小的值//获取matrix数组的当前行当前列的值//两者相加,就是 dp[rowIndex][colIndex]能够得到的最小值dp[rowIndex][colIndex] = Math.min(dp[rowIndex][colIndex -1], dp[rowIndex -1][colIndex]) + matrix[rowIndex][colIndex];}}return dp[row-1][col-1];}以上代码是逐步推导的过程。但是,如果一个100行100列的数组需要推导,而且是要右下角的数据,中间数据是没有必要一直存在的。以上的代码浪费了 100*100的空间,并不是一个好的方式:
分析:
1. 第一行的数据是一定要的,因为根据第一行数据可以推导出第二行的数据
2. 第一列的数据是没有必要一次性全部推导出来的,因为每一个格子只依赖上一行的当前列和当前行的前一列。如果移动到当前行,直接更新当前行的第一列即可。
优化的代码:
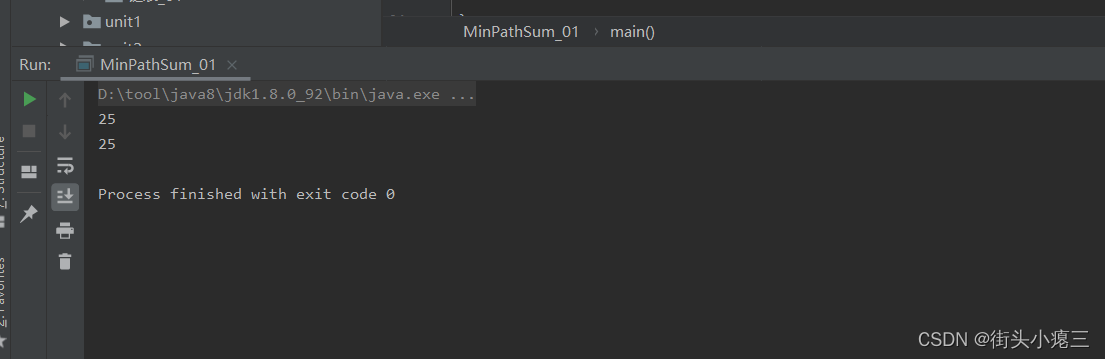
//空间压缩进行优化public static int minSum2 (int[][] matrix){if (matrix == null || matrix.length == 0) {return 0;}//行数int row = matrix.length;//列数int col = matrix[0].length;// 空间压缩。// 二维数组变一维数组。int[] dp = new int[col];//构建dp表的第一行数据dp[0] = matrix[0][0];for (int colIndex = 1; colIndex < col; colIndex++) {//前一列和当前列的累加和,放入dp表dp[colIndex] = dp[colIndex -1] + matrix[0][colIndex];}for (int rowIndex = 1; rowIndex < row; rowIndex++) {//当前行第一列数据dp[0] += matrix[rowIndex][0];for (int colIndex = 1; colIndex < col; colIndex++) {dp[colIndex] = Math.min(dp[colIndex -1], dp[colIndex]) + matrix[rowIndex][colIndex];}}return dp[col -1];}完整代码以及测试结果:
package code03.动态规划_07.lesson4;/*** 给定一个二维数组matrix,一个人必须从左上角出发,最后到达右下角* 沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和* 返回累加和最小值*/
public class MinPathSum_01 {public static int minSum (int[][] matrix){if (matrix == null || matrix.length == 0) {return 0;}//行数int row = matrix.length;//列数int col = matrix[0].length;//如果是100*100规模的二维数组。那么dp的空间开销巨大int[][] dp = new int[row][col];//dp的第一行值只能依赖左边的值dp[0][0] = matrix[0][0];//构建dp表的第一行数据for (int colIndex = 1; colIndex < col; colIndex++) {//前一列和当前列的累加和,放入dp表dp[0][colIndex] = dp[0][colIndex -1] + matrix[0][colIndex];}//构建dp表的第一列数据for (int rowIndex = 1; rowIndex < row; rowIndex++) {//上一列和当前列的累加和,放入dp表dp[rowIndex][0] = dp[rowIndex -1][0] + matrix[rowIndex][0];}for (int rowIndex = 1; rowIndex < row; rowIndex++) {for (int colIndex = 1; colIndex < col; colIndex++) {//先获取上一行当前列 与 当前行的前一列 较小的值//获取matrix数组的当前行当前列的值//两者相加,就是 dp[rowIndex][colIndex]能够得到的最小值dp[rowIndex][colIndex] = Math.min(dp[rowIndex][colIndex -1], dp[rowIndex -1][colIndex]) + matrix[rowIndex][colIndex];}}return dp[row-1][col-1];}//空间压缩进行优化public static int minSum2 (int[][] matrix){if (matrix == null || matrix.length == 0) {return 0;}//行数int row = matrix.length;//列数int col = matrix[0].length;// 空间压缩。// 二维数组变一维数组。int[] dp = new int[col];//构建dp表的第一行数据dp[0] = matrix[0][0];for (int colIndex = 1; colIndex < col; colIndex++) {//前一列和当前列的累加和,放入dp表dp[colIndex] = dp[colIndex -1] + matrix[0][colIndex];}for (int rowIndex = 1; rowIndex < row; rowIndex++) {//当前行第一列数据dp[0] += matrix[rowIndex][0];for (int colIndex = 1; colIndex < col; colIndex++) {dp[colIndex] = Math.min(dp[colIndex -1], dp[colIndex]) + matrix[rowIndex][colIndex];}}return dp[col -1];}public static void main(String[] args) {int[][] arr = {{3,7,9,6},{6,5,3,9},{8,3,1,5},{4,7,9,2}};System.out.println(minSum(arr));System.out.println(minSum2(arr));}}


![[DAU-FI Net开源 | Dual Attention UNet+特征融合+Sobel和Canny等算子解决语义分割痛点]](https://img-blog.csdnimg.cn/direct/8df44dcb68254860bc6cff17be93b66d.png)