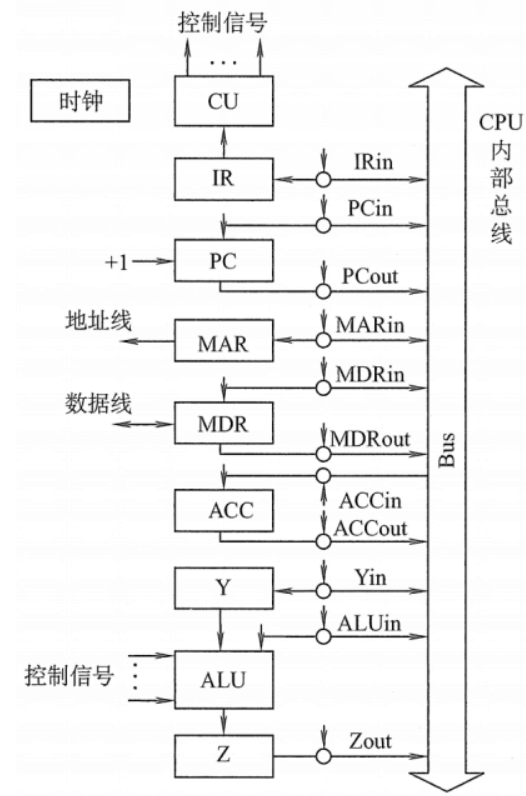
一、实验目的

二、实验内容

三、实验程序

1、

function q1()                                                                                           
N = 1024;  %采样点数
A = 2;  %直流分量
t0 = 5;  %信号时长
dt = t0 / N;  %时间分辨率
fs = 1 / dt;  %系统采样频率
df = 0.001;  %频率分辨率
t = 0 : dt : t0 - dt;
m = cos(2 * pi * t);  %调制信号
c = cos(20 * pi * t);  %载波
fc = 10;  %载波频率
u = (A + m) .* c;  %已调信号
noise_power = 0.1;  %噪声功率
noise_std = sqrt(noise_power);  %噪声标准差
noise = noise_std * randn(1, N);sam = u + noise;  %叠加了噪声的已调信号
[M, m, df1, f] = T2F(m, dt, df, fs);  %求调制信号频谱
[Bw_eq] = signalband(M, df);  %求信号等效带宽
[U, u, df1, f] = T2F(u, dt, df, fs);  %求已调信号频谱figure(1);  %画AM已调信号的时域波形
plot(t, u(1 : length(t)));
xlabel('t');
ylabel('sam(t)');
title('AM已调信号的时域波形');
grid on;figure(2);  %画AM已调信号的频谱
plot(f, abs(fftshift(U)));
xlabel('f'); 
ylabel('|SAM|');
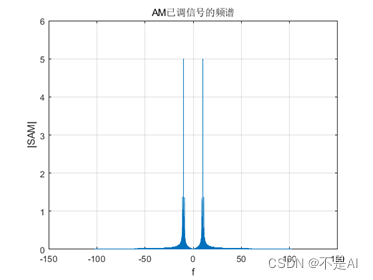
title('AM已调信号的频谱');
grid on;sp = sam .* c; % 与载波相乘后的信号
[spf, sp, df1, f] = T2F(sp, dt, df, fs); %sp的频谱
[LPF, f] = lp_f(length(sp), Bw_eq, df1, fs, 2);DM = LPF .* spf; % 理想低通滤波器输出的频谱[dm] = F2T(DM, fs);  % 滤波器的输出波形
figure;
plot(t, dm(1 : N));dmd = dm(1 : N) -  mean(dm(1 : N));figure;
plot(t, dmd);
xlabel('t');
ylabel('m\^(t)');
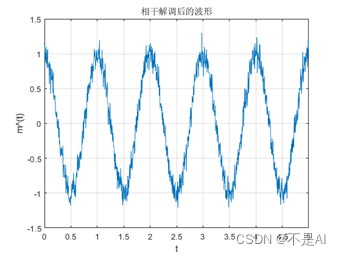
title('相干解调后的波形');
grid on;

2、

function q2()
N = 1024;  % 采样点数
% length(t)
t0 = 5;  % 信号持续时间
dt = t0 / N;  %时间分辨率
fs = 1 / dt;  % 系统采样频率
df = 0.001;  % 频率分辨率
t = 0 : dt : t0 - dt;  % 时间向量
m = sqrt(2) * cos(2 * pi * t);  % 调制信号c = cos(20 * pi * t);  %载波
sdsb = m .* c;  %DSB已调信号
[M, m, df1, f] = T2F(m, dt, df, fs);  %求调制信号频谱
[Bw_eq] = signalband(M, df);  % 调制信号等效带宽
%-------进入信道
noise_power = 0.1;  % 噪声功率
noise_std = sqrt(noise_power);  % 噪声标准差
noise = noise_std * randn(1, N);  % 高斯白噪声
sn = sdsb + noise;  % 叠加了噪声的已调信号figure;  % 画DSB已调信号的时域波形
plot(t, sdsb);
xlabel('t/s');
ylabel('sdsb(t)');
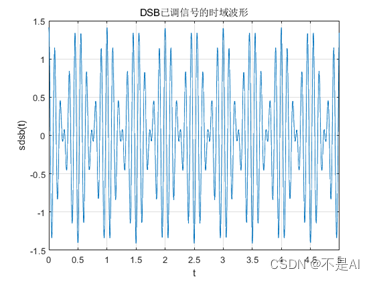
title('DSB已调信号的时域波形');
grid on;Y = fft(sdsb, N);  % 有限长信号sdsb的傅里叶变换
Pyy = abs(Y) .^ 2 / N;  %傅里叶变换模平方的均值
f = 1 / dt * (0 : (N - 1) / 2) / N;  %频率轴figure;  % 画已调信号的功率谱密度
plot(f, Pyy(1 : N / 2));
xlabel('f/Hz');
ylabel('P(f)');
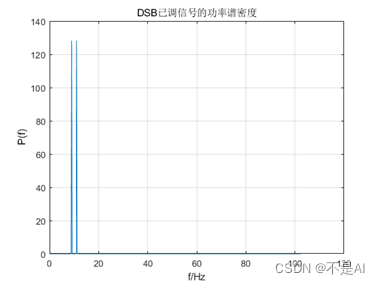
title('DSB已调信号的功率谱密度');
grid on;sp = sn .* c;
[spf, sp, df1, f] = T2F(sp, dt, df, fs); %sp的频谱为spf
[LPF, f] = lp_f(length(sp), Bw_eq, df1, fs, 2);DM = LPF .* spf; % 理想低通滤波器输出的频谱[dm] = F2T(DM, fs);  % 滤波器的输出波形
figure;
plot(t, dm(1 : N));
xlabel('t');
ylabel('m\^(t)');
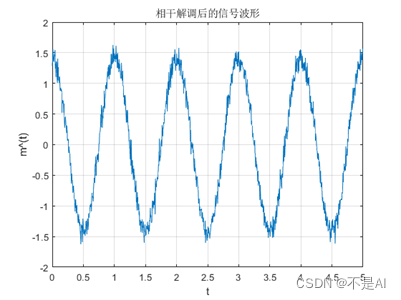
title('相干解调后的信号波形');
grid on;

四、实验结果

1、
（1）、AM已调信号的时域波形：

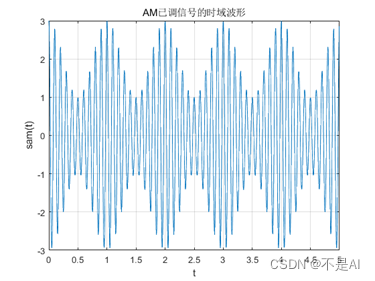
（2）、AM已调信号的频谱：

（3）、相干解调后的波形：

2、
（1）、DSB已调信号的时域波形图：

（2）、DSB已调信号的功率谱密度：

（3）、相干解调后的波形：

五、实验分析

AM调制和DSB调制的区别与联系：
标准调幅是常规双边带调制，简称调幅（AM）。AM信号的时域表达式为：
s_AM (t)=[A_0+m(t)]cosω_c t.
在AM信号中，载波分量并不携带信息，信息完全由边带传送。
双边带信号(DSB)的时域表达式为：
s_DSB (t)=m(t)cosω_c t.

AM信号和DSB信号的带宽都是基带信号带宽f_H的2倍。即
B_AM= B_DSB=2f_H
相比于AM，DSB调制可以节省载波功率：
AM信号的频谱：
S_AM (ω)= πA_0 [δ(ω+ ω_C )+ δ(ω- ω_C )+ 1/2[M(ω+ ω_C )+ M(ω- ω_C )]
DSB信号的频谱：
S_DSB (ω)=1/2[M(ω+ ω_C )+ M(ω- ω_C )]

AM解调和DSB相干解调过程类似，实质都是频谱搬移。解调是调制的反过程，即把在载频位置上的已调信号的频谱搬回到原始基带位置，因此同样可以用相乘器与载波相乘来实现。

注意：AM信号的解调结果中含有直流成分A_0，这时在解调后再加上一个简单隔直流电容即可。