😄😊😆😃😄😊😆😃
开始cpp刷题之旅,多学多练,尽力而为。
先易后难,先刷简单的。

28. 找出字符串中第一个匹配项的下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = “sadbutsad”, needle = “sad”
输出:0
解释:“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = “leetcode”, needle = “leeto”
输出:-1
解释:“leeto” 没有在 “leetcode” 中出现,所以返回 -1 。
这题解法比较多啊,最牛的属于下面第一种解法,借助c++字符串的api。
解法一:find()
class Solution {
public:int strStr(string haystack, string needle) {return haystack.find(needle);}
};
惊呆了老铁,直接返回即可。
看一下提交记录。
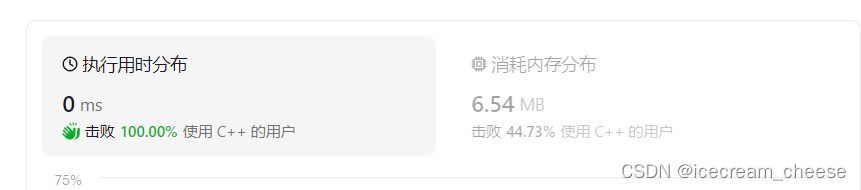
只能说强无敌。
解法二:循环查找
这种方法比较简单直接,从haystack的第一个字符开始遍历在,到haystack的长度减去needle 的长度时截止(因为再查也没有意义,剩下的字符数量小于needle的长度了)。
当找到第一个时就可以结束返回当前的索引了,如果不满足就继续往下查找,但是这种方法明显的,效率比较低下。
class Solution {
public:int strStr(string haystack, string needle) {int targetNum = haystack.size();int currNum = needle.size();for(int i = 0;i+currNum <=targetNum;i++){bool flag= true;for(int j=0;j<currNum;j++){if(haystack[i+j]!=needle[j]){flag = false;break;}}if(flag){return i;}}return -1;}
};
看一下提交记录:

😢 😢 😢 😢 😢 😢 😢 😢
解法三:截取字符串
另外一种方法,直接截取haystack中的字符串,长度为needle的长度,将截取的字符串与needle做比较,如果相同则返回当前i,如果不同则继续,直到最后结束。
class Solution {
public:int strStr(string haystack, string needle) {int targetNum = haystack.size();int currNum = needle.size();for(int i = 0 ; i+currNum<=targetNum;i++){string substr = haystack.substr(i,currNum);if(needle== substr){return i;}}return -1;}
};
好像也挺好理解的,看一下提交记录。
😢 😢 😢 😢 😢 😢 😢 😢
还不如解法二。