逻辑斯蒂回归简介

  逻辑斯蒂回归（Logistic Regression）是一个非常经典的算法，虽然被称为回归，但其实际上是分类模型，并常用于二分类。因为通过逻辑回归模型，我们得到的计算结果是0-1之间的连续数字，可以把它称为“可能性”（概率）,然后，给这个可能性加一个阈值，就成了分类。逻辑回归因其简单、可并行化、可解释强深受工业界喜爱。
  Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计。

逻辑回归拟合函数

  逻辑回归算法的拟合函数，叫做Sigmoid函数，是一个单调可导的函数，通过设置阈值0.5，就可以分为两类
$$\hat{y}=\{\begin{array}{ll}1,& \sigma (x)>0.5\\ 0,& \sigma (x)\le 0.5\end{array}$$

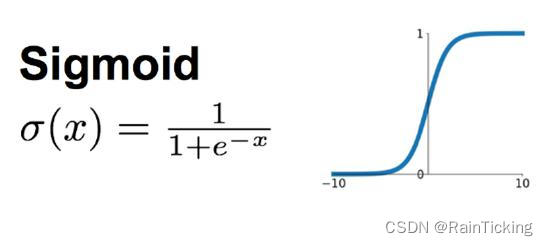
从图形上看，sigmoid曲线就像是被掰弯捋平后的线性回归直线，将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性” 。

Sigmoid函数的输入记为$z$，多元场景下的公式为：$z=w_0{x}_0+w_1{x}_1+w_2{x}_2+...+w_n{x}_n$，采用向量的写法$z=xw$，其中$w_0$是多元函数常数项，而$x_0$的值置为1，便于与$w$矩阵相乘。
$$f(x)=\frac{1}{1+e^{-xw}}$$

最大似然函数估计

在二分类问题中，y只取0或1，可以组合起来表示y的概率：
$P(y)=P(y=1{)}^{y}P(y=0{)}^{1-y}$

加上特征$x$和参数$w$后，表示为：
$P(y|x,w)=P(y=1|x,w{)}^y[1-P(y=1|x,w){]}^{1-y}$

把$P(y=1|x,w)=\frac{1}{1+e^{-xw}}$代入上式得：
$P(y|x,w)=(\frac{1}{1+e^{-xw}}{)}^y(1-\frac{1}{1+e^{-xw}}{)}^{1-y}$

因$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$是实际观测的数据，而不同事件是相互独立的，那么它们同时发生的概率为${\prod }_{i=1}^{n}P(y_i|x_i,w)$。即似然函数为：
$$L(w)=\prod _{i=1}^{n}P(y_i|x_i,w)=\prod _{i=1}^n(\frac{1}{1+e^{-x_{i}w}}{)}^{y_i}(1-\frac{1}{1+e^{-x_{i}w}}{)}^{1-y_i}$$
如此，问题变为了参数$w$在取什么值时，$L(w)$取得极大值。
$$\hat{w}=arg\underset{w}{\max }L(w)$$

交叉熵损失函数

  损失函数是用于衡量预测值与实际值的偏离程度，即模型预测的错误程度。也就是说，这个值越小，认为模型效果越好，举个极端例子，如果预测完全精确，则损失函数值为0。
  我们要做的是$L(w)$取得极大值，反过来$-L(w)$取得极小值，与损失函数的要求相同。因连乘不易取极值，需对$L(w)$取对数后，在取相反数，这样就成为了交叉熵损失函数：
$$J(w)=-\log L(w)=-\sum _{i=1}^n[y_i\log P(y_i)+(1-y_i)\log (1-P(y_i))]$$
其中：
$y_i$ : 表示样本$i$的标记（label），正类为1，负类为0
$P(y_i)$：表示样本$i$预测为正类的概率

梯度下降法求解

对于Sigmoid函数 $f(z)=\frac{1}{1+e^{-z}}$，求导得：
$f^{\prime }(z)=(\frac{1}{1+e^{-z}}{)}^{\prime }=-\frac{(e^{-z}{)}^{\prime }}{(1+e^{-z}{)}^2}=\frac{e^{-z}}{(1+e^{-z}{)}^2}$

这还不算完，我们发现 $1-f(z)=\frac{e^{-z}}{1+e^{-z}}$，而$f^{\prime }(z)$正好可以拆分为$\frac{e^{-z}}{1+e^{-z}}\cdot \frac{1}{1+e^{-z}}$，也就是说：
$f^{\prime }(z)=f(z)\cdot (1-f(z))$

已知$z=xw$，而$x$是实际观测数据，未知的是$w$，所以后面是对$w$求导，记：
$$\frac{\partial J(w)}{\partial w}=\frac{\partial J(w)}{\partial f(z)}\ast \frac{\partial f(z)}{\partial z}\ast \frac{\partial z}{\partial w}$$

其中：
$\begin{array}{rl}\frac{\partial J(w)}{\partial f(z)}& =-[y\log f(z)+(1-y)\log (1-f(z)){]}^{\prime }\\ & =-(\frac{y}{f(z)}+(1-y)\frac{-1}{1-f(z)})\\ & =-(\frac{y}{f(z)}+\frac{y-1}{1-f(z)})\end{array}$

$\begin{array}{rl}\frac{\partial f(z)}{\partial z}& =f(z)(1-f(z))\end{array}$

$\begin{array}{rl}\frac{\partial z}{\partial w}& =x\end{array}$

综上所得：
$$\begin{array}{rl}\frac{\partial J(w)}{\partial w}& =-(\frac{y}{f(z)}+\frac{y-1}{1-f(z)})\ast f(z)(1-f(z))\ast x\\ & =-(y-f(z))\ast x\\ & =-(y-\frac{1}{1+e^{-xw}})\ast x\end{array}$$

因此，梯度上升迭代公式为：
$$w:=w+\alpha (y-\frac{1}{1+e^{-xw}})\ast x$$

梯度下降算法过程：

1. 初始化$w$向量的值，即 ${\Theta }_0$，将其代入G得到当前位置的梯度；
2. 用步长α乘以当前梯度，得到从当前位置下降的距离；
3. 更新 ${\Theta }_1$，其更新表达式为 ${\Theta }_1={\Theta }_0-\alpha G$；
4. 重复以上步骤，直到更新到某个 ${\Theta }_k$，达到停止条件，这个 ${\Theta }_k$就是我们求解的参数向量。

逻辑斯蒂回归分布

定义：设X是连续随机变量，X服从逻辑斯蒂分布是指X具有下列分布函数和密度函数：
$$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu )/\gamma }}$$

$$f(x)=F^{\prime }(x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma (1+e^{-(x-\mu )/\gamma }{)}^2}$$

式中，$\mu$为位置参数，$\gamma >0$为形状参数。

Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的$Sigmoid$函数就是 Logistic 的分布函数在$\mu =0,\gamma =1$的特殊形式。

逻辑斯蒂回归实战

首先，下载数据集 testSet.txt，数据集链接：https://pan.baidu.com/s/1rJm0Ok_9OfrsEktVqhGoCQ?pwd=47db ，提取码：47db

from numpy import *# 加载数据集
def loadDataSet():datas = []; classLabels = []fr = open('testSet.txt')for line in fr.readlines():lineArr = line.strip().split()datas.append([1.0, float(lineArr[0]), float(lineArr[1])])classLabels.append(int(lineArr[2]))return datas,classLabelsdef sigmoid(inX):return 1.0/(1+exp(-inX))# return 0.5 * (1 + tanh(0.5 * inX))# 梯度上升算法
def gradAscent(datas, classLabels):dataMat = mat(datas)             #convert to NumPy matrixlabelMat = mat(classLabels).transpose() #convert to NumPy matrixm,n = shape(dataMat)alpha = 0.001  # 步长maxCycles = 500  # 迭代次数weights = ones((n,1))for k in range(maxCycles):       #heavy on matrix operationsh = sigmoid(dataMat*weights) #matrix mult,h为列向量，元素数为nerror = (labelMat - h)       #vector subtractionweights = weights + alpha * dataMat.transpose()* error #matrix multreturn weights# 画出数据集和逻辑回归最佳拟合直线
def plotBestFit(weights):import matplotlib.pyplot as pltdataMat,labelMat=loadDataSet()dataArr = array(dataMat)n = shape(dataArr)[0] xcord1 = []; ycord1 = []xcord2 = []; ycord2 = []for i in range(n):if int(labelMat[i])== 1:xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])else:xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])fig = plt.figure()ax = fig.add_subplot(111)ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')ax.scatter(xcord2, ycord2, s=30, c='green')x = arange(-3.0, 3.0, 0.1)y = (-weights[0]-weights[1]*x)/weights[2]ax.plot(x, y.T)plt.xlabel('X1'); plt.ylabel('X2')plt.show()# 训练梯度下降算法并画出最佳拟合直线
datas,classLabels = loadDataSet()
weights = gradAscent(datas, classLabels)
plotBestFit(weights)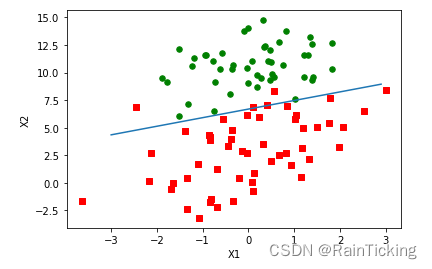

从疝气病症预测病马的死亡率

疝病是描述马胃肠痛的术语，数据集中包含368个样本和28个特征。使用Logistic回归估计马疝病的死亡率步骤如下：

1. 收集数据：给定数据文件。
2. 准备数据：用Python解析文本文件并填充缺失值。
3. 分析数据：可视化并观察数据。
4. 训练算法：使用优化算法，找到最佳的系数。
5. 测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否回退到训练阶段，通过改变迭代的次数和步长等参数来得到更好的回归系数。
6. 使用算法：实现一个简单的命令行程序来收集马的症状并输出预测结果。

需要说明的是，除了部分指标主观和难以测量外，该数据存在的另一个问题是大约30%的值是缺失的。一些可选的处理缺失值的做法有：

• 使用可用特征的均值来填补缺失值
• 使用特殊值来填补缺失值，如-1
• 忽略有缺失值的样本
• 使用相似样本的均值填补缺失值
• 使用另外的机器学习算法预测缺失值

这里，选择实数0来替换所有缺失值，这样在更新系数时，0值不会有影响，而且对结果的预测不具有任何倾向性。若类别标签缺失则直接丢弃。原始数据集经过预处理后保存成两个文件：horseColicTest.txt 和 horseColicTraining.txt。

from numpy import *def sigmoid(inX):return 0.5 * (1 + tanh(0.5 * inX))# 随机梯度上升算法
def stocGradAscent0(datas, classLabels):m,n = shape(datas)alpha = 0.01weights = ones(n)   #initialize to all onesfor i in range(m):h = sigmoid(sum(datas[i]*weights))error = classLabels[i] - hweights = weights + alpha * error * datas[i]return weights# 改进的随机梯度上升算法
def stocGradAscent1(datas, classLabels, numIter=150):m,n = shape(datas)weights = ones(n)   #initialize to all onesfor j in range(numIter):dataIndex = list(range(m))for i in range(m):alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constanth = sigmoid(sum(datas[randIndex]*weights))error = classLabels[randIndex] - hweights = weights + alpha * error * datas[randIndex]del(dataIndex[randIndex])return weights# 逻辑回归分类函数
def classifyVector(inX, weights):prob = sigmoid(sum(inX*weights))if prob > 0.5: return 1.0else: return 0.0def colicTest():frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')trainingSet = []; trainingLabels = []for line in frTrain.readlines():currLine = line.strip().split('\t')lineArr =[]for i in range(21):lineArr.append(float(currLine[i]))trainingSet.append(lineArr)trainingLabels.append(float(currLine[21]))trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)errorCount = 0; numTestVec = 0.0for line in frTest.readlines():numTestVec += 1.0currLine = line.strip().split('\t')lineArr =[]for i in range(21):lineArr.append(float(currLine[i]))if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]):errorCount += 1errorRate = (float(errorCount)/numTestVec)print ("the error rate of this test is: %f" % errorRate)return errorRatedef multiTest():numTests = 10; errorSum=0.0for k in range(numTests):errorSum += colicTest()print ("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))# 训练并检验
multiTest()

the error rate of this test is: 0.358209
the error rate of this test is: 0.328358
the error rate of this test is: 0.283582
the error rate of this test is: 0.388060
the error rate of this test is: 0.313433
the error rate of this test is: 0.268657
the error rate of this test is: 0.283582
the error rate of this test is: 0.358209
the error rate of this test is: 0.388060
the error rate of this test is: 0.283582
after 10 iterations the average error rate is: 0.325373