【回溯算法】n-皇后

题目来源

n-皇后

题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

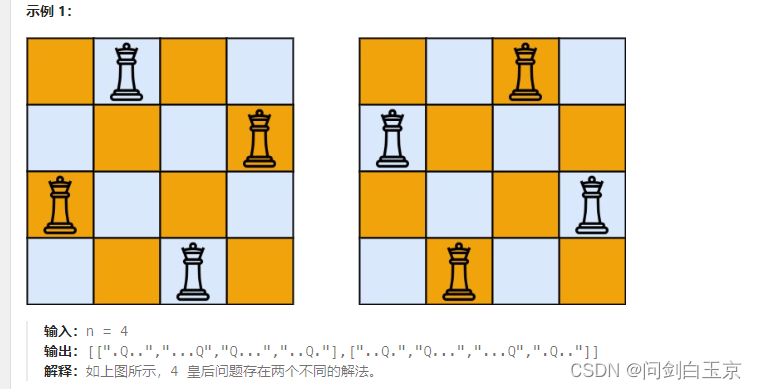
给你一个整数 n ，返回所有不同的n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中'Q' 和 '.'分别代表了皇后和空位。

示例

在这里插入图片描述

思路

这道题是根据labuladong算法秘籍刷到的

回溯的过程可以看作是决策树中做决策与撤回决策，决策就是走向下一层，撤回决策就是返回。
在这里插入图片描述

核心代码：

void backtrack(当前选择, 剩余选择列表) {if (当前选择产生的结果满足结束递归条件) {return;}for (选择 in 剩余选择列表) {//做出当前选择st[选择] = true;// 进入下一层决策树backtrack(选择 ,剩余选择列表);// 撤回选择st[选择] = false;}
}

在本题中决策树的每一层表示棋盘上的每一行；每个节点可以做出的选择是，在该行的任意一列放置一个皇后。
回溯的过程中，当前考虑行的前面所有行已经做过选择

回溯函数

/**@description: 回溯函数，如果当前递归到row行，前row-1行已经放置好皇后@param: borad - 棋盘@param: row - 当前到第几行了*/void backtrack(vector<string> &borad, int row) {if (row == borad.size()) {res.push_back(borad);return;}int n = borad[row].size();for (decltype(borad.size()) i = 0; i < n; ++ i) {// 判断row 行 i 列可不可以放皇后if (!valid(borad, row, i)) {// 不能放continue;}// 放置皇后borad[row][i] = 'Q';// 继续下一行棋盘backtrack(borad, row + 1);// 不放borad[row][i] = '.';}}

valid函数用于判断当前位置是否可以放置皇后：
如果当前位置所在行、列、正对角线、负对角线有放置皇后，那么当前位置就不可以放置皇后了

valid函数

/**@param: board  棋盘@param: row  行@param: line 列@return bool类型，true表示可以放，false表示不可以放*/bool valid(vector<string> &board, int row, int line) {int n = board.size();// 同一行是否放了皇后for (int j = 0; j < line; ++ j) {if (board[row][j] == 'Q') return false;}// 同一列是否放了皇后for (int i = 0; i < row; ++ i) {if (board[i][line] == 'Q') return false;}// 左斜线是否放了皇后int b = line - row;for (int i = 0; i < row; ++i) {int j = i + b;if (j < 0) continue;if (board[i][j] == 'Q') return false;}// 右斜线是否放了皇后b = row + line;for (int i = 0; i < row; ++ i) {int j = b - i;if (j < 0) continue;if (board[i][j] == 'Q') return false;}// 都没有放皇后return true;}

这里解释一下为什么正对角、负对角这么计算:将棋盘想象成下面样子

正对角的情况如下：
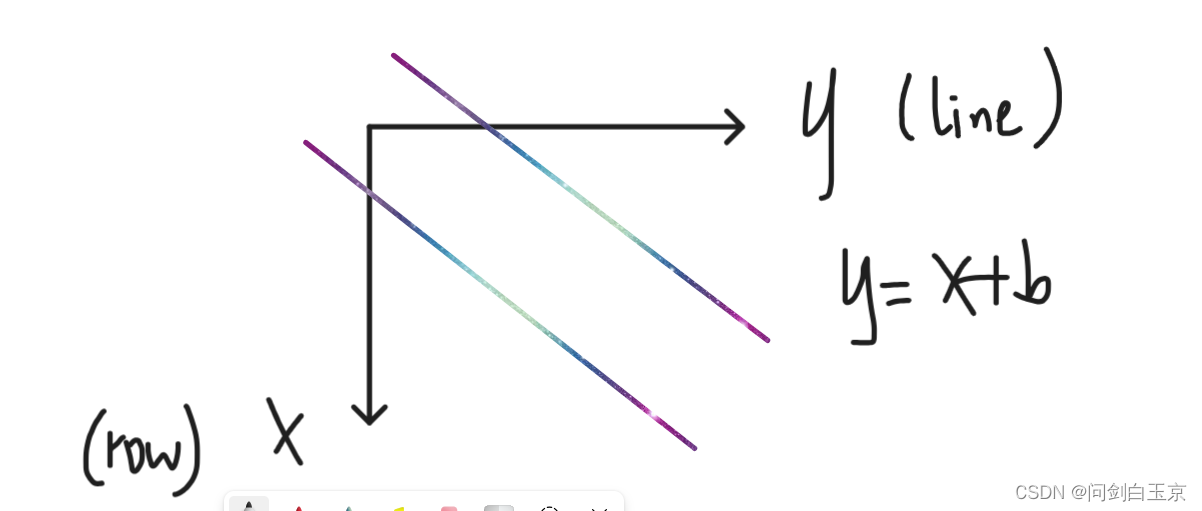
在这里插入图片描述
对于当前位置(row, line)，我们可以确定这条对角线：计算b = y - x;
所以b = line - row, 然后从 0 ~ row - 1 计算每一个 y值，然后要保证y值为正

负对角同理

完整代码

class Solution {
public:vector<vector<string>> res;vector<vector<string>> solveNQueens(int n) {vector<string> borad(n, string(n, '.'));// 回溯backtrack(borad, 0);return res;}/**@description: 回溯函数，如果当前递归到row行，前row-1行已经放置好皇后@param: borad - 棋盘@param: row - 当前到第几行了*/void backtrack(vector<string> &borad, int row) {if (row == borad.size()) {res.push_back(borad);return;}int n = borad[row].size();for (decltype(borad.size()) i = 0; i < n; ++ i) {// 判断row 行 i 列可不可以放皇后if (!valid(borad, row, i)) {// 不能放continue;}// 放置皇后borad[row][i] = 'Q';// 继续下一行棋盘backtrack(borad, row + 1);// 不放borad[row][i] = '.';}}/**@param: board  棋盘@param: row  行@param: line 列@return bool类型，true表示可以放，false表示不可以放*/bool valid(vector<string> &board, int row, int line) {int n = board.size();// 同一行是否放了皇后for (int j = 0; j < line; ++ j) {if (board[row][j] == 'Q') return false;}// 同一列是否放了皇后for (int i = 0; i < row; ++ i) {if (board[i][line] == 'Q') return false;}// 左斜线是否放了皇后int b = line - row;for (int i = 0; i < row; ++i) {int j = i + b;if (j < 0) continue;if (board[i][j] == 'Q') return false;}// 右斜线是否放了皇后b = row + line;for (int i = 0; i < row; ++ i) {int j = b - i;if (j < 0) continue;if (board[i][j] == 'Q') return false;}// 都没有放皇后return true;}
};