目录
- max-flow 和 min-cut
- 流网络 Flow network
- 最小割 Min-cut
- 最大流 Max-flow
- Greedy algorithm
- Ford–Fulkerson algorithm
- 剩余网络 Residual network
- Ford–Fulkerson algorithm算法流程
- 最大流最小割理论 max-flow min-cut theorem
- 容量扩展算法 capacity-scaling algorithm
- 时间复杂度分析 Analysis of Ford–Fulkerson algorithm
- 优化:选择合适的增广路径
- 选择足够大瓶颈容量的增广路径算法:Capacity-scaling algorithm
- 寻找最短增广路径算法:BFS
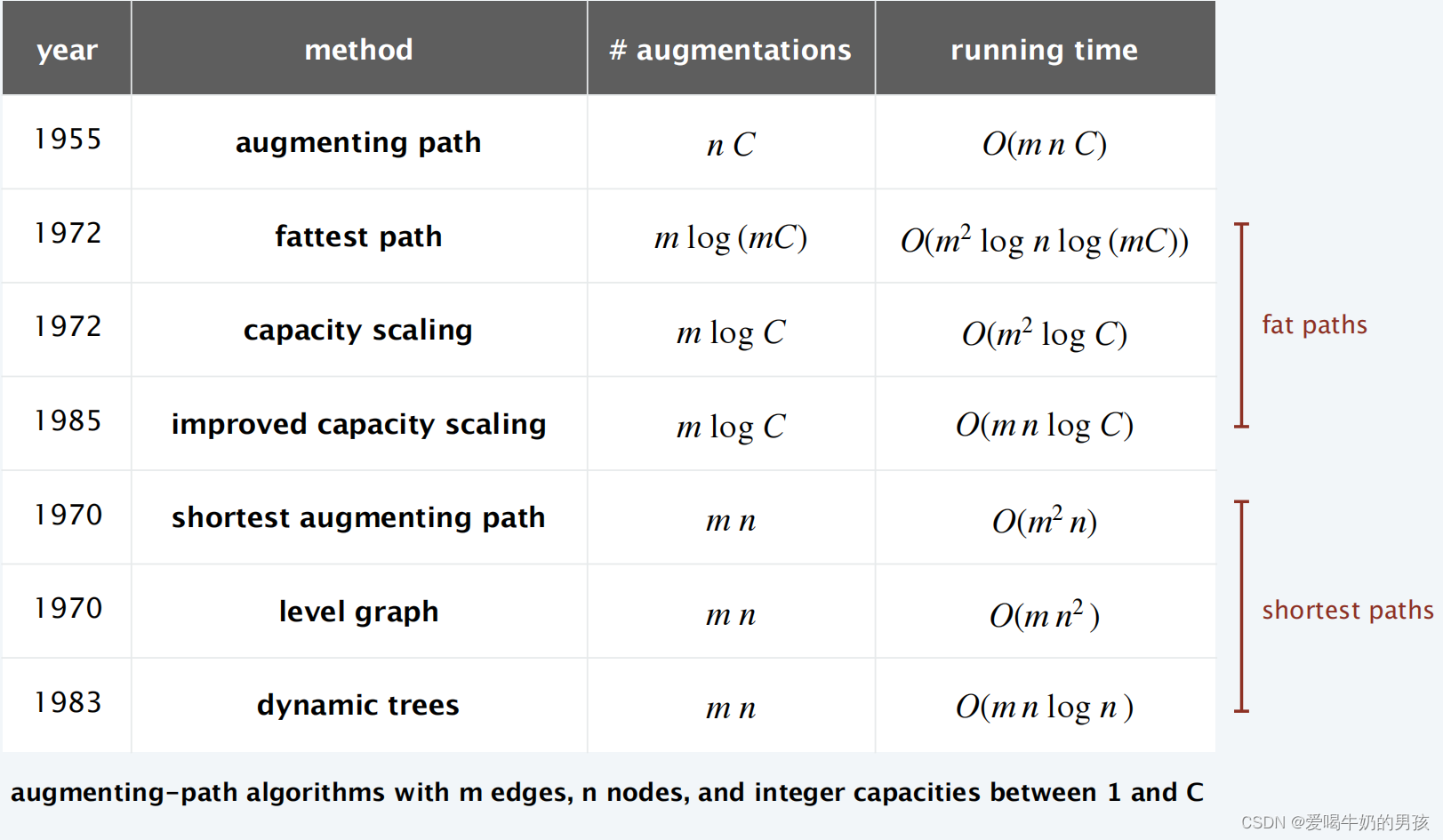
- 其他算法的时间复杂度
max-flow 和 min-cut
流网络 Flow network
流网络定义为一个元组 G = ( V , E , s , t , c ) G=(V, E, s, t, c) G=(V,E,s,t,c)
- V:流网络中点的集合
- s:源点,没有流量输入,只有流量输出, s ∈ V s ∈ V s∈V
- t:汇点,没有流量输出,只有流量输入, t ∈ V t ∈ V t∈V
- E:流网络中边的集合
- c ( e i ) c(e_i) c(ei):边的容量, c ( e i ) > = 0 c(e_i) >= 0 c(ei)>=0
最小割 Min-cut
割 (s-t cut) 被定义为一个点的划分 ( A , B ) (A, B) (A,B),其中 s ∈ A s ∈ A s∈A, t ∈ B t ∈ B t∈B。即将流网络的所有点,分成两个部分 A 和 B。
割的容量(capacity):定义为 从 A 到 B 线段的容量之和: c a p ( A , B ) = ∑ e o u t o f A c ( e ) cap(A, B) = \sum_{ e\ out\ of\ A} c(e) cap(A,B)=∑e out of Ac(e)
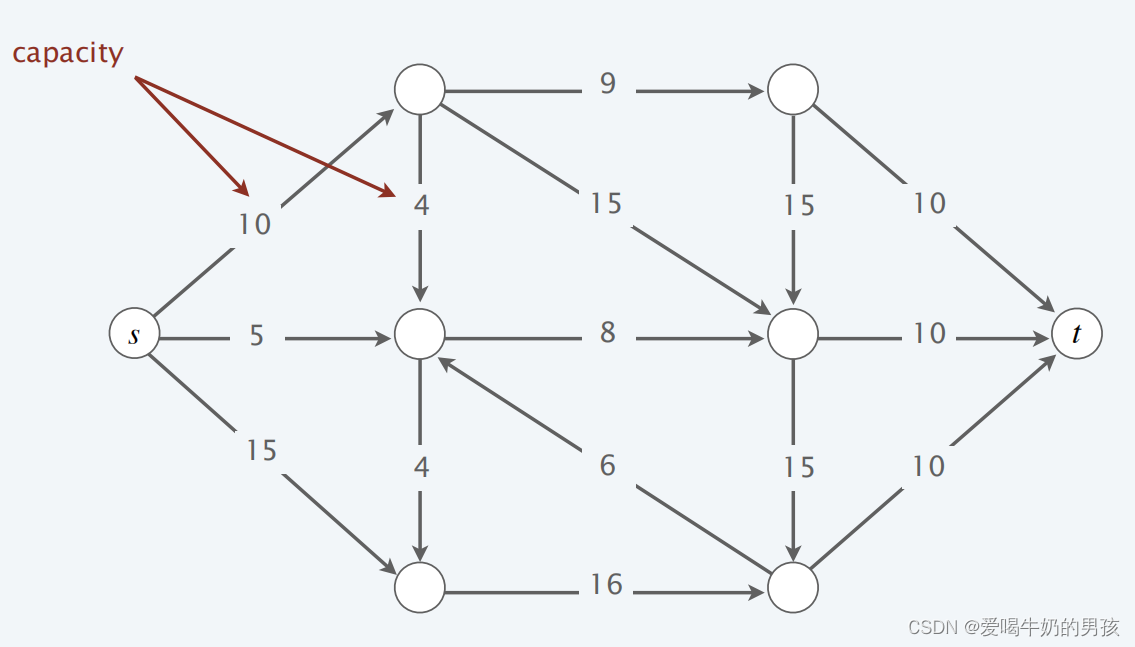
如下图所示,A 仅包含 s,因此 c a p ( A , B ) = 10 + 5 + 15 = 30 cap(A, B) = 10 + 5 + 15 = 30 cap(A,B)=10+5+15=30。
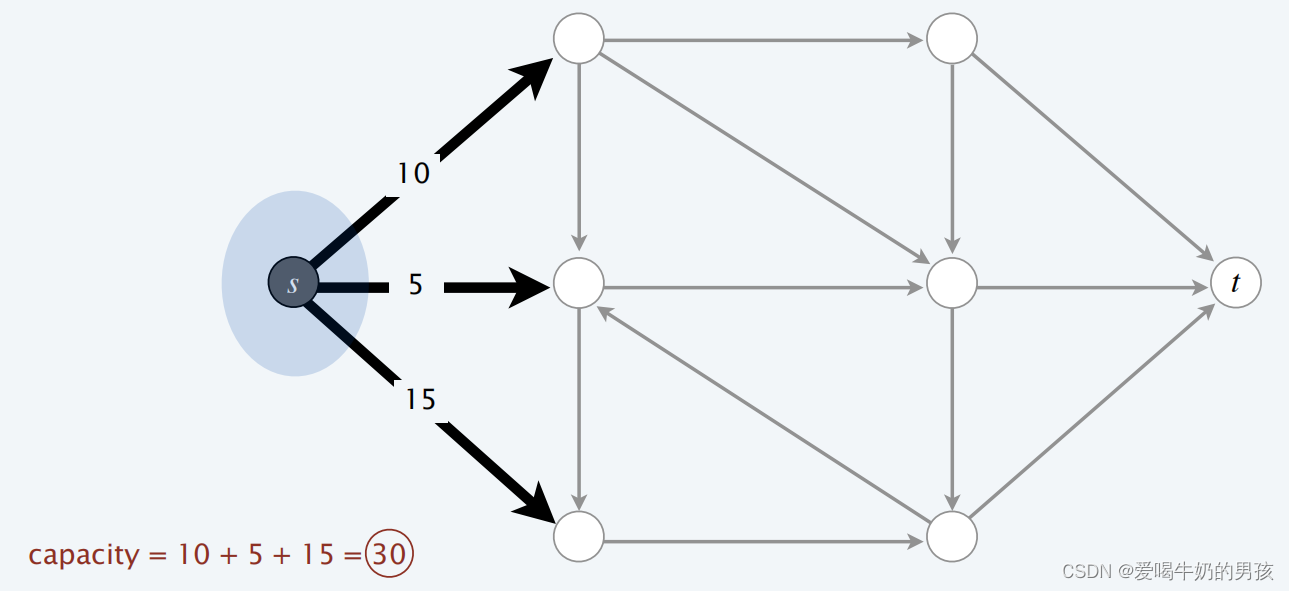
下图割的容量: c a p ( A , B ) = 10 + 8 + 16 = 34 cap(A, B) = 10 + 8 + 16 = 34 cap(A,B)=10+8+16=34。

最小割(Min-cut):即整个流网络中,容量最小的那个割(st cut).
最大流 Max-flow
定义 流 st-flow (flow) 中 f f f 是一个满足以下条件的函数:
- 每一个 e ∈ E e ∈ E e∈E,均有 0 < = f ( e ) < = c ( e ) 0 <= f(e) <= c(e) 0<=f(e)<=c(e) ,即流量小于等于容量。
- 对于任意 v ∈ V − s , v v ∈ V - {s , v} v∈V−s,v,即出去源点和汇点的其他点: ∑ e i n t o v f ( e ) = ∑ e i o u t o f v f ( e ) \sum_{e\ in\ to\ v}f(e) = \sum_{e\ iout\ of\ v}f(e) ∑e in to vf(e)=∑e iout of vf(e),即出去源点和汇点,所有进入点的流量等于流出点的容量。
进入v的流量: 5 + 5 + 0 = 13 5 + 5 + 0 =13 5+5+0=13、流出v的流量: 10 + 0 = 10 10 + 0 = 10 10+0=10
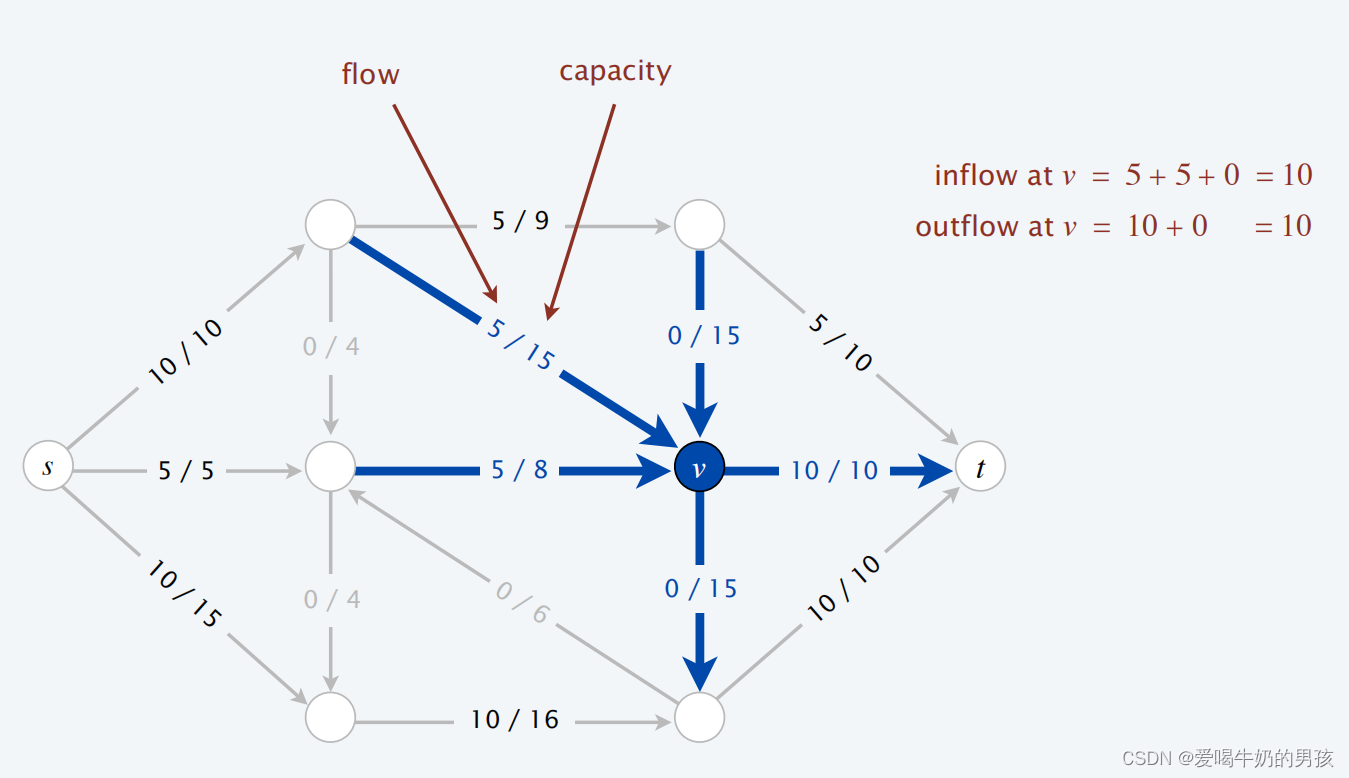
流 flow 的值定义为: v a l ( f ) = ∑ e o u t o f s f ( e ) − ∑ e i n t o s f ( e ) val(f) = \sum_{e\ out\ of\ s}f(e) - \sum_{e\ in\ to\ s}f(e) val(f)=∑e out of sf(e)−∑e in to sf(e)
下图中,网络流的值为: 10 + 5 + 10 = 25 10 + 5 + 10 = 25 10+5+10=25

最大流Max-flow:流网络中,值最大的流即为最大流。
最大流问题 和 最小割问题 问题是等价的。
Greedy algorithm
增广路径 Augmenrt Path:从 源点 s 到 汇点 t 的一条简单路径,路径上任意一条边均满足 f ( e ) < c ( e ) f(e) < c(e) f(e)<c(e)。
阻塞流 Blocking Flow:如果一个 流 flow,找不到增广路径,则该流称为阻塞流。最大流一定是阻塞流,但阻塞流不一定是最大流。
贪心算法的流程:
- 初始流上,任意的 e ∈ E , f ( e ) = 0 e ∈ E, f(e) = 0 e∈E,f(e)=0。
- 进行流量的增加:
- 寻找该流上的增广路径 P
- 增加 增广路径 P 上各个边的流量
- 重复流量增加的步骤,直至该流变成阻塞流
贪心算法得到的阻塞流并不一定是最大流,因为贪心在寻找增广路径之后,直接沿着找到的增广路径进行流量的增加,之后就继续找下一条增广路径。没有考虑增广路径找错的情况,没有办法减少增广路径上的错误流量。
Ford–Fulkerson algorithm
剩余网络 Residual network
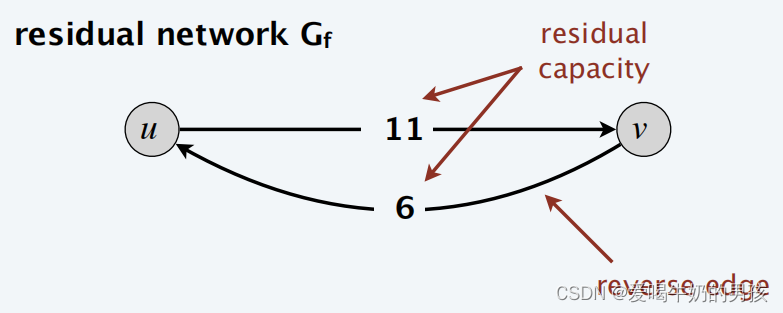
原始边 Original edge: e = ( u , v ) ∈ E e = (u, v) ∈ E e=(u,v)∈E,且边上的流量: f ( e ) f(e) f(e)、边上的容量: c ( e ) c(e) c(e)
反向边: e r e v e r s e = ( v , u ) e^{reverse} = (v, u) ereverse=(v,u)
剩余容量: c f ( e ) = { c ( e ) − f ( e ) e ∈ E f ( e r e v e r s e ) e r e v e r s e ∈ E c_f(e)=\begin{cases} c(e)-f(e) &e∈E \\ f(e^{reverse})&e^{reverse}∈E \end{cases} cf(e)={c(e)−f(e)f(ereverse)e∈Eereverse∈E
剩余网络 Residual network: G = ( V , E f , s , t , c f ) G = (V, E_f, s, t, c_f) G=(V,Ef,s,t,cf):
- E f = { e : f ( e ) < c ( e ) } ∪ { e : f ( e r e v e r s e ) > 0 } E_f = \{e: f(e) < c(e)\} ∪ \{e: f(e^{reverse}) > 0\} Ef={e:f(e)<c(e)}∪{e:f(ereverse)>0}
定义增广路径 的 瓶颈容量 为 增广路径上,最小的剩余容量。
Ford–Fulkerson algorithm算法流程
- 初始流上,任意的 e ∈ E , f ( e ) = 0 e ∈ E, f(e) = 0 e∈E,f(e)=0。
- 进行剩余图上流量的增加:
- 寻找该剩余图上的增广路径 P
- 增加 增广路径 P 上各个边的流量,同时在剩余图上添加反向变
- 重复流量增加的步骤,直至该流变成阻塞流
算法的流量增减都是在剩余图上进行操作的。
最大流最小割理论 max-flow min-cut theorem
定义 f f f 为任意的 流 flow, ( A , B ) (A, B) (A,B) 为任意的 割 cut,则 f f f的流量大小等于流过 ( A , B ) (A,B) (A,B)的流量。
v a l ( f ) = ∑ e o u t o f A f ( e ) − ∑ e i n t o A f ( e ) val(f) = \sum_{e \ out \ of A}f(e) - \sum_{e \ in \ to\ A}f(e) val(f)=e out ofA∑f(e)−e in to A∑f(e)

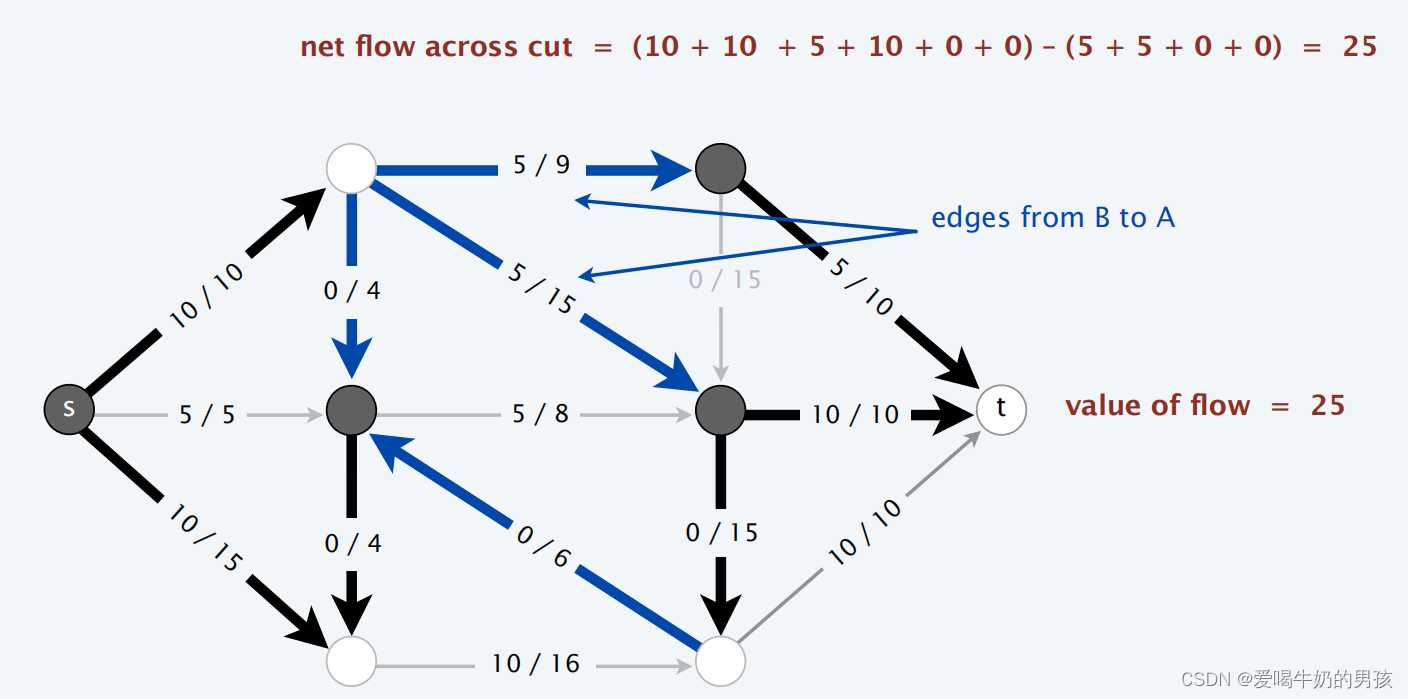
v a l ( f ) = ∑ e o u t o f A f ( e ) − ∑ e i n t o A f ( e ) v a l ( f ) = ∑ e o u t o f s f ( e ) − ∑ e i n t o s f ( e ) = ∑ v ∈ A ( ∑ e o u t o f A f ( e ) − ∑ e i n t o A f ( e ) ) = ∑ e o u t o f A f ( e ) − ∑ e i n t o A f ( e ) val(f) = \sum_{e \ out \ of A}f(e) - \sum_{e \ in \ to\ A}f(e)\\ val(f) = \sum_{e \ out \ of s}f(e) - \sum_{e \ in \ to\ s}f(e)\\ = \sum_{v ∈ A}( \sum_{e \ out \ of A}f(e) - \sum_{e \ in \ to\ A}f(e))\\ = \sum_{e \ out \ of A}f(e) - \sum_{e \ in \ to\ A}f(e) val(f)=e out ofA∑f(e)−e in to A∑f(e)val(f)=e out ofs∑f(e)−e in to s∑f(e)=v∈A∑(e out ofA∑f(e)−e in to A∑f(e))=e out ofA∑f(e)−e in to A∑f(e)
同时定义 f f f 为任意的 流 flow, ( A , B ) (A, B) (A,B) 为任意的 割 cut,则 v a l ( f ) < = c a p ( A , B ) val(f) <= cap(A, B) val(f)<=cap(A,B)
v a l ( f ) = ∑ e o u t o f A f ( e ) − ∑ e i n t o A f ( e ) < = ∑ e o u t o f A f ( e ) < = ∑ e o u t o f A c ( e ) = c a p ( A , B ) val(f) = \sum_{e \ out \ of A}f(e) - \sum_{e \ in \ to\ A}f(e)<= \sum_{e \ out \ of A}f(e) <= \sum_{e \ out \ of A}c(e) = cap(A, B) val(f)=e out ofA∑f(e)−e in to A∑f(e)<=e out ofA∑f(e)<=e out ofA∑c(e)=cap(A,B)
定义 f f f 为任意的 流 flow, ( A , B ) (A, B) (A,B) 为任意的 割 cut。如果 v a l ( f ) = c a p ( A , B ) val(f) = cap(A, B) val(f)=cap(A,B),那 f f f 一定是最大流, ( A , B ) (A, B) (A,B)一定是最小割。
Max-flow min-cut theorem:Value of a max flow = capacity of a min cut.
容量扩展算法 capacity-scaling algorithm
时间复杂度分析 Analysis of Ford–Fulkerson algorithm
假设 流网络 中所有的边上的容量均为整数,且 范围是 1~C。
则 FFA算法中,每一条边的流量和剩余容量也都是正整数。
假设 f ∗ f* f∗ 是某流网络的最大流,则该流网络中最大流流量 v a l ( f ∗ ) < = n C val(f*) <= nC val(f∗)<=nC。
又每次增广路径最少也会增加 1 的流量,假设使用 BFS、DFS来寻找增广路径,时间复杂度为 O ( m ) O(m) O(m),则Ford–Fulkerson algorithm 的时间复杂度最坏为: T ( n ) = O ( m n C ) T(n) = O(mnC) T(n)=O(mnC)
T ( n ) = O ( m n C ) T(n) = O(mnC) T(n)=O(mnC)的情况出现在,每一次找到的增广路径都只能增加一个容量,例如:
如果时间复杂度为 O ( m n C ) O(mnC) O(mnC),那么该时间复杂度并非多项式时间的,需要根据边的数量以及容量的大小来判断是否能在一定时间内解决。
优化:选择合适的增广路径
出现上述非多项式时间的时间复杂度的情况的原因:每一次增广路径都只增加1个流量,即瓶颈容量为1的增广路径。
因此我们可以选择更合适的增广路径。
- 最大瓶颈容量的增广路径
- 足够大的瓶颈容量的增广路径
- 最短路径的增广路径
选择足够大瓶颈容量的增广路径算法:Capacity-scaling algorithm
算法大致流程:
- 首先遍历所有的边,得到最大容量/2,将其设置为当前瓶颈容量下限 k
- 在剩余图中寻找瓶颈容量大于等于 k 的增广路径
- 如果找到了就执行FFA算法
- 如果找不到了,就将 k 减小到原来的一半
- 一直执行寻找增广路径的循环,直至 k 变为1,此时所有的增广路径都能正常寻找到。
算法伪代码:

m:边的数量
n:点的数量
C:容量的上限
使用该算法寻找增广路径,总的寻找最大流的时间复杂度: T ( n ) = O ( m 2 l o g C ) T(n) = O(m^2logC) T(n)=O(m2logC)
寻找最短增广路径算法:BFS
使用队列,不断扩展下一个节点,当到达 t ,此路径即为最短路。
算法伪代码:

m:边的数量
n:点的数量
C:容量的上限
使用该算法寻找增广路径,总的寻找最大流的时间复杂度: T ( n ) = O ( m 2 n ) T(n) = O(m^2n) T(n)=O(m2n)
其他算法的时间复杂度