目录
第一章 数据库系统概述
第二章 关系代数
第四章 关系数据库理论
第五章 数据库设计
第六章 数据库管理系统
第八章 事务管理
第一章 数据库系统概述
1.1三级模式
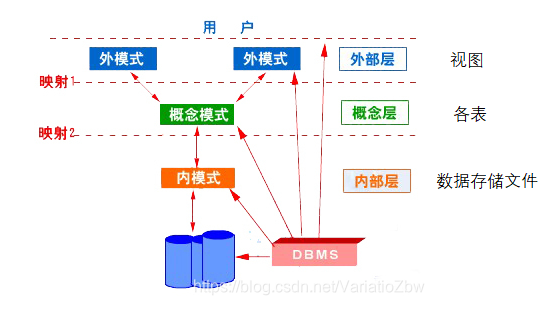
①外模式:它为特定的应用程序或用户群体提供了一个数据视图,这个视图是独立于数据库其他用户的。
②概念模式:由数据库管理员使用SQL语句(DDL)来定义的表,供数据库管理员使用。
③内模式:数据在数据库内部的物理结构和存储方式,说明了数据如何在存储介质上存储。
1.2 两级映射
①外模式-概念模式的映射:当概念模式(表)发生变化时,通过修改映射关系(视图-表),可以使得外模式保持不变,从而应用程序也不需要改变,体现了逻辑独立性。
②概念模式-内模式的映射:保证了物理独立性,即数据库的存储结构发生变化时,不会影响到应用程序。数据库管理员可以在表结构不变的情况下,修改内模式。
第二章 关系代数

第四章 关系数据库理论
4.1 如何求属性集闭包?
依据:根据公理系统的自反律(X决定自身的子集)、传递律(A--->B、B---->C可以得出A--->C)可以求解属性集的闭包。


4.2如何求最小函数依赖集?
原则:右(右边分解为单一属性)、中(去本求包)、左(左边最小化)

4.3 如何求候选码?
①给定关系模式R (U, F)。将R的所有属性分为L, R, LR和N四类。其中
L表示属性只在函数依赖左边出现:
R表示属性只在函数依赖右边出现;
LR表示属性既在左边出现,又在右边出现;
N表示函数依赖左右都未出现。
②令X=L U N, Y=LR求X的闭包,若X的闭包包含了R表的所有属性,则X为R的唯一候选码,转(5) 。
tip: 因为X已经是R表的候选码了,所以X再与Y中的每个属性组合的闭包肯定也等于属性全集U此时所求的候选码就是超码。属于多余的,因此没必要在求(XA)。
③Y中选取任意一个属性A,求(XA)的闭包,若它包含了R的全部属性,则是候选码。调换属性,反复进行这个过程,直到试完Y中的所有属性。
④如果已找出所有的候选码,转(5) ,否则在Y中后面依次选取2个属性,3个属性,.... 求他们的闭包,若其闭包包含R的全部属性, 则是候选码。
⑤结束算法,输出候选码。
4.4 如何将关系模式分解成3NF范式?
步骤:
1、求F的最小函数依赖集,合并左边相同的函数依赖(依据合并性)。
2、将最小函数依赖集中每个函数依赖组成一个表。
3、如果构成的各表中没有一个表中包含R的某个候选键,就选取R表中的一个后选键作为一张表放入模式集中(求最小依赖集F的候选码)。
4.5 如何判断表满足第几范式?
1NF范式: 表中每个单元格都是不能在分割的最小单元(横平竖直)
2NF范式:表中不存在非主属性(普通列)对候选码的部分函数依赖,而是对候选码的完全函数依赖。
3NF范式:表中不存在非主属性列对候选码的传递函数依赖(没有中间属性)。
BCNF范式:表中所有函数依赖都写出来,如果函数依赖集各元素左边都包含候选码则此表满足BCNF范式。
第五章 数据库设计
5.1 E-R图
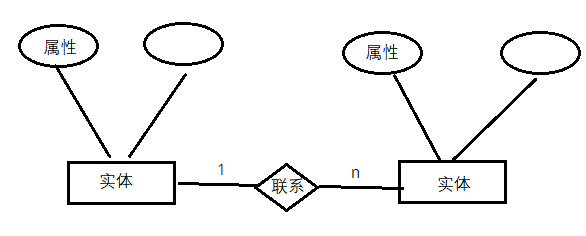
5.2 E-R图转换为关系模式
总结:
①一个实体对应一张表,表的属性就是与实体相连的属性。
②所有联系都可以独立作为一张表,其属性由“两端实体主码+自身属性”,主码因联系类型不同而异。
③1:1、1:n的联系都能合并,合并后的表属性由“加入到表的属性+另端主码+联系自身属性”。其合并后表的主码为:加入到的实体表中的主码。
- 1:1
联系独立作为一张表: 两端相连实体主码+联系自身属性。
主码:从两端实体的主码中任选一个作为关系表的主码。
联系与其他表合并:另端实体主码+联系自身属性,放到要加入到的表中。
主码:加入表的主码
- 1:N
联系独立:两端相连实体的主码+联系自身属性。
主码:N端主码作为独立表的主码
联系合并到N端表中:另端实体主码+联系自身属性。
主码:加入表的主码。即N端的主码作为表的主码
- N:M
联系只能独立单独作为一张表,其表的属性由“联系两端相连实体的主码+联系自身属性”。其表的主码为:两端实体的主码组合在一起共同作为联系表的主码。
第六章 数据库管理系统
6.1 查询优化
基本原则:尽量减少查询过程中的中间结果,从而以较少的时间和空间开销取得所需的查询结果。
优化策略:
①尽可能先做选择运算,允许的情况下在优先执行投影。
②将先笛卡尔积后选择的查询转化为连接运算。
③把投影运算和选择运算同时进行。
④让投影运算与其前后的其它运算同时进行。
⑤在执行连接前先对关系做适当的预处理,如:在连接属性上建立索引。
第八章 事务管理
8.1 什么是事务
为了满足特定的需求而由一系列数据库操作的SQL语句组成的集合。这些SQL操作语句要么全部执行成功,要么全部执行失败(微信转账)。
8.2 封锁
所谓封锁就是事务T在对数据对象操作之前如:表、记录先对其进行加锁。加锁后事务T就会对数据对象有一定的控制,而在事务T释放掉数据对象的锁前不允许其它事务对数据对象进行操作了(类似Java中的文件锁)。
①排它锁:事务T在对数据对象加X锁后,只有事务T可以对数据对象进行读、写。其它事务无法对数据对象在进行加锁,也不能读、写此数据对象。
②共享锁:事务T在对数据对象加S锁后,不管是其本身还是其它事务都只能对数据对象只读而无法写入,其它事务可以在对数据对象加S锁但不能加X锁。