前言
💓作者简介: 加油,旭杏,目前大二,正在学习C++,数据结构等👀
💓作者主页:加油,旭杏的主页👀⏩本文收录在:再识C进阶的专栏👀
🚚代码仓库:旭日东升 1👀
🌹欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖
学习目标:
我们大家应该都了解归并排序,而且可以很容易地将归并排序的递归形式写出,但是在面试或其他情况下,可能会考察我们非递归的写法,在这一篇博客中,我们会记录到如何写出归并排序非递归的写法,以及另一种排序方法:计数排序。
学习内容:
通过上面的学习目标,我们可以列出要学习的内容:
- 归并排序的非递归写法
- 计数排序的原理和代码写法
一、归并排序的非递归写法
1.1 归并排序(稳定排序)的复习
归并排序利用分治的思想,将一个数组划分为两个有序的部分,然后在合并成一个有序的数组,利用递归的思想,但是,在一个要排序的数组中,不可能只分割一次就将数组分为两个有序的部分,我们要一直递归地分,直到一个区间中只剩下一个数时,就是有序的。类似于下图所示:

代码如下:
void mergesort(int a[], int left, int right)
{if (left >= right)return;int mid = (left + right) >> 1;mergesort(a, left, mid);mergesort(a, mid + 1, right);int l = left, r = mid + 1, cnt = left;while (l <= mid && r <= right){if (a[l] < a[r]){tmp[cnt++] = a[l++];}else{tmp[cnt++] = a[r++];}}while (l <= mid){tmp[cnt++] = a[l++];}while (r <= right){tmp[cnt++] = a[r++];}for (int i = left; i <= right; i++){a[i] = tmp[i];}
}1.2 应该用什么数据结构来实现非递归写法呢?
在快速排序中,我们使用栈来模拟非递归的排序,因为在递归的过程中,编译器会调用栈空间来实现递归的过程,但是在用栈来模拟快速排序的非递归的时候,我们可以发现,我们自己利用栈来实现的快速排序是不能回溯的,所以并不是真正意义上的递归过程。
而在归并排序的过程中,我们可以发现我们只有在递归完成之后,在进行比较和排序,如果我们使用栈来模拟的话,是没有回溯的过程的,所以利用栈来模拟的话,我们只能将数组分割开,而不能将有序数组进行合并,因此,我们不能使用栈来模拟实现归并排序的非递归写法。
那我们应该用什么来模拟实现归并排序的非递归写法呢?在之前,我们会写一个斐波那契数列,我们是利用递归来写的,但是,利用递归的斐波那契数列算不了很大的数字,我们可以使用循环或者是记忆化搜索来优化算法,因为记忆化搜索是涉及动态规划,我们之后在来细说。
循环就是我们来解决归并排序非递归写法的思路。我们可以先通过斐波那契数列的优化来了解一下循环是如何进行的。因为斐波那契数列的递归过程是从后往前推的,但是我们已经知道了前两个数是多少,而递归过程是通过回溯来知道每一位对应的数是多少。而归并排序也是从后面往前推的,所以我们可以使用循环来实现。
1.3 循环实现非递归的过程
我们可以先来两个区间两个区间来合并,然后将要合并的区间大小倍增。要注意边界问题,代码去下:
void merge(int a[], int left, int mid, int right)
{// 合并过程就不介绍了int l = left, r = mid + 1, cnt = left;while (l <= mid && r <= right){if (a[l] <= a[r]){tmp[cnt++] = a[l++];}else{tmp[cnt++] = a[r++];}}while (l <= mid){tmp[cnt++] = a[l++];}while (r <= right){tmp[cnt++] = a[r++];}for (int i = left; i <= right; i++){a[i] = tmp[i];}
}void sortNonR(int a[], int left, int right)
{int n = right - left + 1;int l = 0, m = 0, r = 0;for (int gap = 1; gap < n; gap *= 2){l = 0;while (l < n) // 注意边界问题{m = l + gap - 1;if (m + 1>= n) // 如果第二个区间的左边界超过了所给数组的下标,我们可以breakbreak;r = min(l + (gap * 2) - 1, n - 1);merge(a, l, m, r);l = r + 1;}}
}二、归并排序的另一个用途(外排序)
像我们之前学习过的排序算法,可以按照排序算法能够排序在哪里存放的数据来划分为:内排序和外排序。而归并排序是唯一一个外排序的算法,归并排序既可以内排序,也可以外排序。换句人话:归并排序既可以排序内存中的数据,也可以排序硬盘中的数据。所以归并排序有一个非常大的用途,就是排序超级多的数据(存储在硬盘中)。
我们可以先将1G的数据输入到内存中排序,然后再讲文件按照1G的大小分割,然后进行归并即可。这里的思想是:我们在归并时,不一定非要是一个数字,可以是其他单位。
三、 计数排序的原理和缺陷(非比较排序)
计数排序,顾名思义就是将数字进行统计,一个数字在数组中出现了多少次。然后按顺序进行输出即可。看起来还是比较简单的,但是这个排序不常用,之后在说缺点。
3.1 计数排序的原理
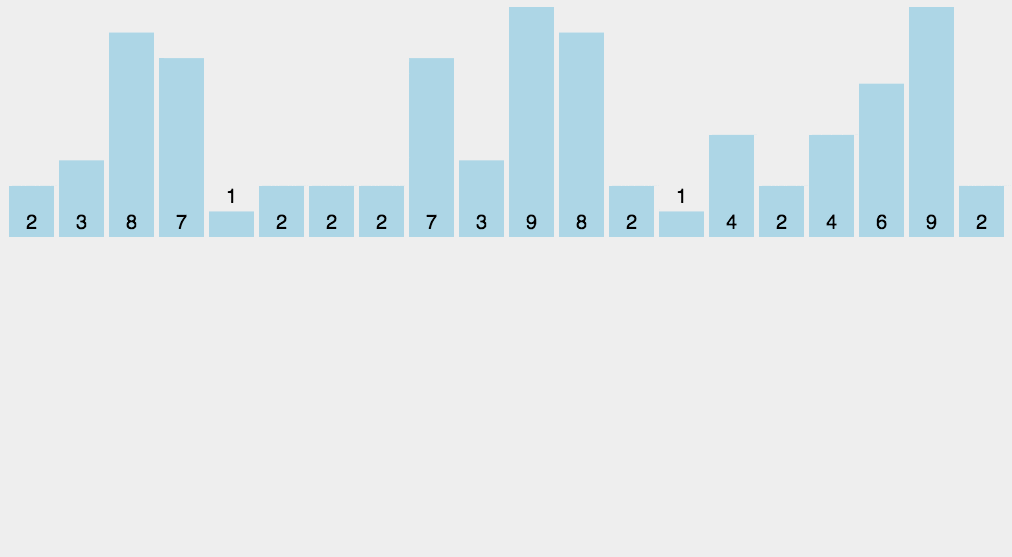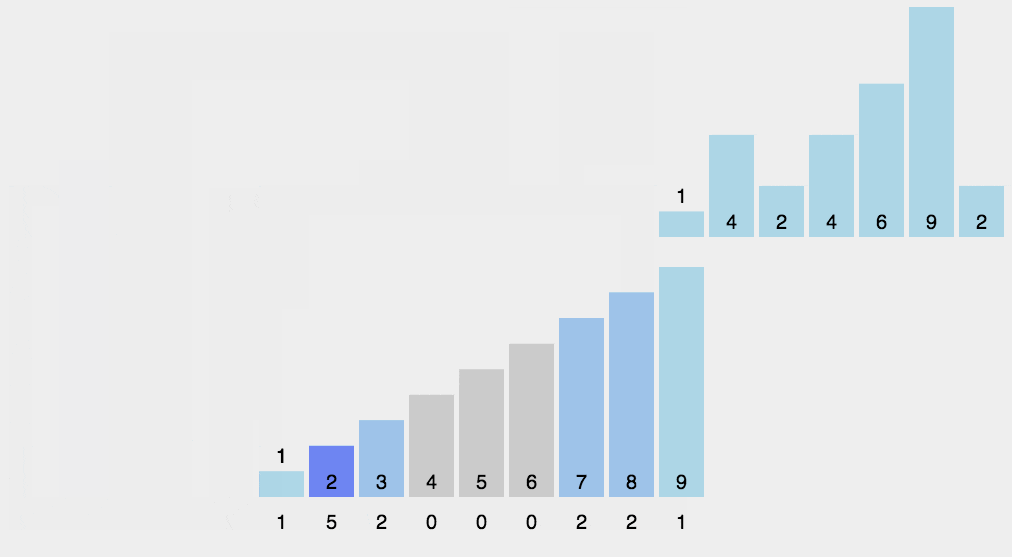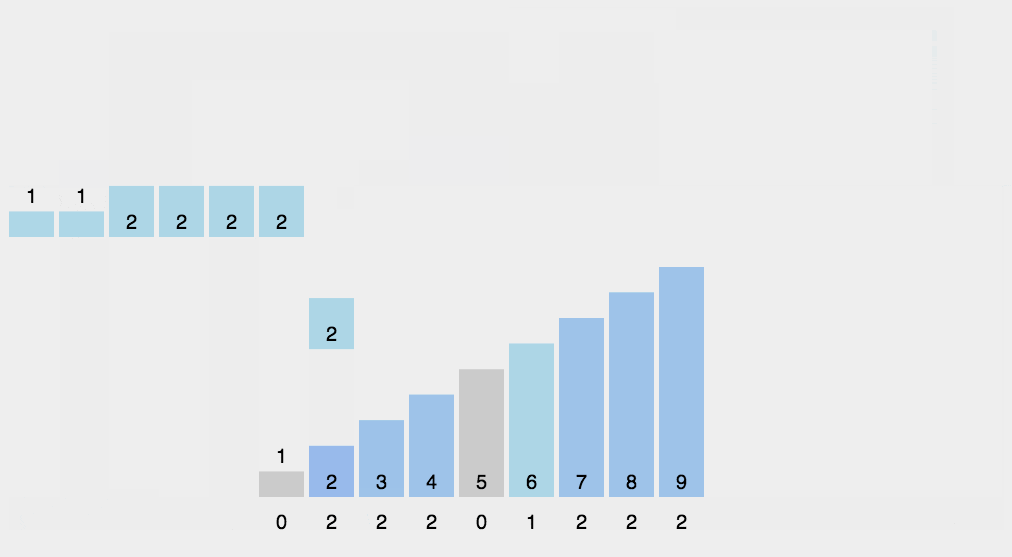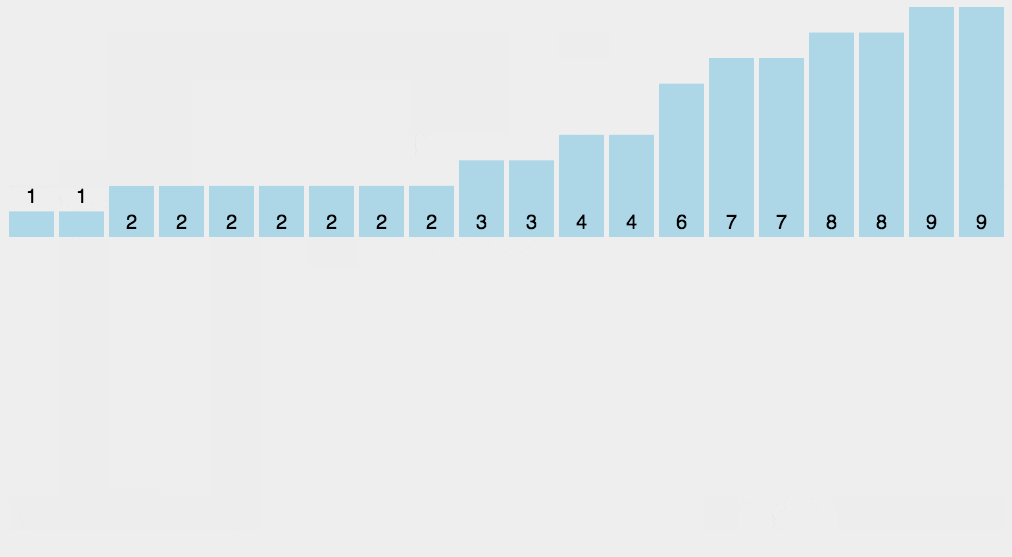
这个排序很像哈希的思想,就是利用额外的空间来统计每一个数字出现的个数。我们可以使用数组,其范围是最大的数字的大小,其优点就是效率极高。代码如下:
// 非优化版本
void Countsort(int a[], int n)
{int max = 0;for (int i = 0; i < n; i++){if (max < a[i])max = a[i];}// 统计出最大值int* tmp = (int*)malloc(sizeof(int) * max + 1);for (int i = 0; i < n; i++)tmp[a[i]]++;int cnt = 0;for (int i = 0; i <= max; i++)while (tmp[i]--)a[cnt++] = i;
}
3.2 计数排序的缺陷
- 不适合分散的数据,更适合于集中的数据
- 不适合浮点数,字符串,结构体数据排序,只适合整数
- 不适合数据过大的整数排序
3.3 代码优化
根据缺陷,我们可以将要排序的数组的最小值和最大值找出,然后根据最大值和最小值来确定数组的大小。这样我们即可以排序正数,也可以排序负数。优化代码如下:
void Countsort(int* a, int n)
{int min = 0, max = 0;for (int i = 0; i < n; i++){if (min > a[i])min = a[i];if (max < a[i])max = a[i];}// 统计出最大,最小值int range = max - min + 1;int* tmp = (int*)calloc(range, sizeof(int));for (int i = 0; i < n; i++){tmp[a[i] - min]++;}int cnt = 0;for (int i = 0; i < range; i++){while (tmp[i] --){a[cnt++] = i + min;}}
}