目录
- 复向量 Complex vectors
- 复矩阵 Complex matrices
- 傅里叶变换 Fourier transform
- 快速傅里叶变换 Fast Fourier transform
实矩阵也可能有复特征值,因此无法避免在矩阵运算中碰到复数,本讲学习处理复数矩阵和复向量。
最重要的复矩阵是傅里叶矩阵,它用于傅里叶变换。而对于大数据处理快速傅里叶变换(FFT)显得更为重要,它将傅立叶变换的矩阵乘法中运算的次数从 n 2 n^2 n2次降至 n l o g 2 n nlog2^n nlog2n 次。
复向量 Complex vectors
对于给定的复向量 z = [ z 1 z 2 . . . z n ] ∈ C n z =\begin{bmatrix} z_1\\z_2\\...\\z_n \end{bmatrix}∈C^n z= z1z2...zn ∈Cn ,其元素中有复数,因此 z T z z^Tz zTz 无法给出向量的长度。
例如 [ 1 i ] \begin{bmatrix} 1 & i \end{bmatrix} [1i] [ 1 i ] \begin{bmatrix} 1 \\ i \end{bmatrix} [1i] =0,则定义 ∣ z ∣ 2 = z ‾ T z = ∣ z 1 ∣ 2 \begin{vmatrix} z \end{vmatrix}^2 =\overline{z}^Tz =\begin{vmatrix} z_1 \end{vmatrix}^2 z 2=zTz= z1 2 + ∣ z 2 ∣ 2 \begin{vmatrix} z_2 \end{vmatrix}^2 z2 2+ . . . + ∣ z n ∣ 2 ...+\begin{vmatrix} z_n \end{vmatrix}^2 ...+ zn 2为向量长度。因此向量 [ 1 i ] \begin{bmatrix} 1 \\ i \end{bmatrix} [1i]的长度就是 [ 1 − i ] [ 1 i ] = 2 \begin{bmatrix} 1 & -i \end{bmatrix}\begin{bmatrix} 1 \\ i \end{bmatrix} =2 [1−i][1i]=2,记 ∣ z ∣ 2 \begin{vmatrix} z \end{vmatrix}^2 z 2 = z ‾ T z \overline{z}^Tz zTz = z H z z^Hz zHz ,
H 来自于“Hermite”。 与之相似,内积的定义也变为 y H x = y ‾ T x y^Hx =\overline{y}^Tx yHx=yTx = y 1 ‾ x 1 \overline{y_1}x_1 y1x1 + y 2 ‾ x 2 \overline{y_2}x_2 y2x2 + . . . + y 1 ‾ x 1 ...+\overline{y_1}x_1 ...+y1x1
复矩阵 Complex matrices
上一讲中讲到了对于复矩阵 A,若有 A ‾ T = A \overline{A}^{_T}=A AT=A 则复矩阵 A 的特征值为实数。这种复矩阵被称为埃尔米特矩阵(Hermitian matrixes,又译作“厄米特矩阵”或者“厄米矩阵”)。转置共轭记作 A H = A ‾ T = A A^{_H}=\overline{A}^{_T}=A AH=AT=A。
例如矩阵 [ 2 3 + i 3 − i 5 ] \begin{bmatrix} 2 & 3+i \\ 3-i & 5 \end{bmatrix} [23−i3+i5]为埃尔米特矩阵。它具有实数特征值和正交的特征向量。由性质可知埃尔米特矩阵对角线均为实数。
此处向量标准正交的意思是
q j ‾ T q k = { 0 j ≠ k 1 j = k \overline{q_j}^{_T}q_k= \left\{ \begin{align*} &0 j≠k\\ &1 j=k \end{align*} \right. qjTqk={0j=k1j=k 用 n 个标准正交的复向量作为列向量可以构造一个矩阵 Q,则有 Q T Q = I = Q H Q Q^TQ=I=Q^HQ QTQ=I=QHQ。这个复空间的正交矩阵称为酉矩阵(unitary matrix)。
傅里叶变换 Fourier transform
傅里叶级数是将周期函数或者信号变换为不同频率的三角函数的和函数。
f ( x ) = a 0 + a 1 c o s x + b 1 s i n x + a 2 c o s 2 x + b 2 s i n 2 x + . . . f(x) = a_0 + a_1cosx + b_1sinx +a_2cos2x +b_2sin2x + ... f(x)=a0+a1cosx+b1sinx+a2cos2x+b2sin2x+...
在电子工程或者计算机科学中,n x n矩阵的行和列从第0行和第0列开始计数,最后到第 n-1 行和第 n-1 列。我们在讨论傅里叶矩阵的时候遵从这种习惯。
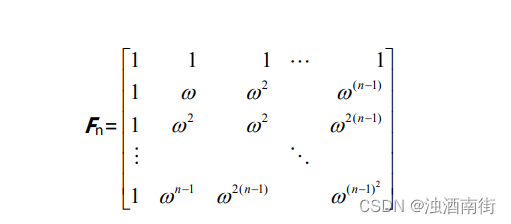
( F n ) j k = ω j k (F_n)_{jk}=ω^{jk} (Fn)jk=ωjk,傅里叶矩阵为对称矩阵 F n = F n T F_n=F_n^T Fn=FnT。矩阵中的 ω n = 1 , ω = e x p ( i 2 π / n ) ω^n=1,ω=exp(i2π/n) ωn=1,ω=exp(i2π/n)。矩阵的列向量正交。ω的方次分布在复平面的单位元上,只是幅角不同。当 n=4 时, ω 4 = 1 , ω = e x p ( i 2 π / 4 ) = i ω^4=1,ω=exp(i2π/4)=i ω4=1,ω=exp(i2π/4)=i。
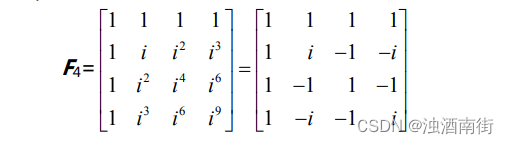
从矩阵可以得到一个四点(离散的)傅里叶变换,它的逆矩阵就是反傅里叶变换。因为傅里叶矩阵列向量正交,所以其逆矩阵很容易计算。实际上这个矩阵可以分解成一系列稀疏矩阵,并且它们的逆矩阵都很容易得到。
计算可知列向量的模不是 1,矩阵除以 2 之后,向量标准正交: 1 4 F 4 H F 4 = I \frac{1}{4}F_4^HF_4 = I 41F4HF4=I。它的逆矩阵就是共轭转置。
快速傅里叶变换 Fast Fourier transform
64 阶傅里叶矩阵 F 64 F_{64} F64中的 ω 64 ω_{64} ω64与 32 阶傅里叶矩阵 F 32 F_{32} F32的元素 ω 32 ω_{32} ω32相比,幅角是其一半, ( ω 64 ) 2 = ω 32 (ω_{64})^2=ω_{32} (ω64)2=ω32。可以从分块矩阵运算找到两者的联系:

P 的效果是使得所乘的向量 x 中序数为奇数的分量如 x 1 x_1 x1, x 3 x_3 x3, x 5 x_5 x5等提到前面,而偶数分量 x 2 x_2 x2, x 4 x_4 x4等放到后面。
计算 64 阶傅里叶变换(傅里叶矩阵乘以向量)的计算量是 6 4 2 64^2 642,而等式右侧的计算量是 2 × 3 2 2 2×32^2 2×322(两个 32 阶的傅里叶矩阵)再加上一些修正项,修正项主要来自于与对角矩阵 D 的乘法,大约为 32 次。继续对 F 32 F_{32} F32进行分解,计算的运算量再一次下降变为 2 × ( 2 × 1 6 2 + 16 ) + 32 2×(2×16^2+16)+32 2×(2×162+16)+32。连续进行拆分,傅里叶矩阵的尺寸变化依次为 64、32、16、8、4、2、1,经过 l o g 2 64 log_264 log264 次分解,最后仅剩修正项的运算, l o g 2 64 × 32 log_264×32 log264×32次。对于 n 阶矩阵,可将 n 2 n^2 n2次计算降至 ( n / 2 ) l o g 2 n (n/2)log_2n (n/2)log2n。例如对于 1024 阶矩阵,运算量从 1024×1024 降至 5×1024。