一、逻辑回归
应用场景:解决二分类问题
1、sigmoid函数
1. 公式:
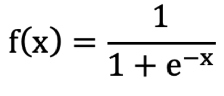
2. 作用:把 (-∞,+∞) 映射到 (0, 1)
3. 数学性质:单调递增函数,拐点在x=0,y=0.5的位置
4. 导函数公式:f ′(x) = f(x) (1 – f(x))
2、相关概念
概率:事件发生的可能性
联合概率:两个或多个随机变量同时发生的概率
条件概率:表示事件A在另外一个事件B已经发生条件下的发生概率,P( A | B )
极大似然估计:根据 观测到的结果 来估计模型算法中的未知参数,即通过极大化概率事 件,来估计最优参数
对数函数:如果a^b = N (a > 0,b != 1),那么 b 叫做以 a 为底 N 的对数。
性质:(a,M,N > 0)
![]()
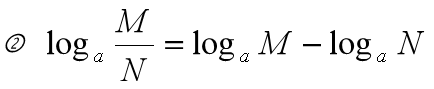
![]()
3、概念
一种分类模型,把线性回归的输出,作为逻辑回归的输入,输出是(0, 1)之间的值
4、假设函数
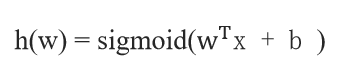
5、损失函数:对数似然损失

工作原理:真实类别对应的位置,概率值越大越好
6、API
sklearn.linear_model.LogisticRegression ( solver = ' liblinear ',penalty = ' l2 ',C = 1.0 )
solver:损失函数优化方法( liblinear 对小数据集场景训练速度更快,sag 和 saga 对大数据集更 快一些。)
penalty:正则化的种类,L1 或者 L2
C:正则化力度
tips:默认将类别数量少的当做正例,sag、saga 支持 L2 正则化或者没有正则化,liblinear 和 saga 支持 L1 正则化
二、模型评估
1、混淆矩阵
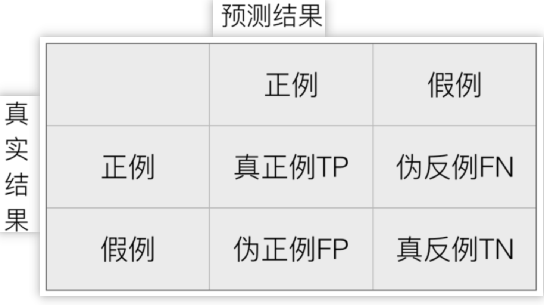
真正例 TP:True Positive,伪反例 FN:False Negative
伪正例 FP:False Positive,真反例 TN:True Negative
TP + FN + FP + TN = 总样本数量
1. 导包:from sklearn.metrics import confusion_matrix
2. 使用:result = confusion_matrix ( y_true,y_pred1,labels = labels)
from sklearn.metrics import confusion_matrixresult = confusion_matrix ( y_true,y_pred1,labels = labels)2、精确率 ( Precision )
概述:查准率,对正例样本的预测准确率

计算方法:

1. 导包:from sklearn.metrics import precision_score
2. 使用:result = precision_score(y_true,y_pred1,pos_label = ' 恶性 ' )
from sklearn.metrics import precision_scoreresult = precision_score(y_true,y_pred1,pos_label = ' 恶性 ' )3、召回率 ( Recall )
概述:查全率,指的是预测为真正例样本占所有真实正例样本的比重

计算方法:
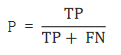
1. 导包:from sklearn.metrics import recall_score
2. 使用:result = recall_score(y_true,y_pred1,pos_label = ' 恶性 ' )
from sklearn.metrics import recall_scoreresult = recall_score(y_true,y_pred1,pos_label = ' 恶性 ' )4、F1- score
概述:对模型的精度 (Precision)、召回率 (Recall) 都有要求,评估综合预测能力 ( 精确率和 召回率 的调和平均数 )
计算方法:

1. 导包:from sklearn.metrics import f1_score
2. 使用:result = f1_score ( y_true,y_pred1,pos_label = ' 恶性 ' )
from sklearn.metrics import f1_scoreresult = f1_score ( y_true,y_pred1,pos_label = ' 恶性 ' )5、ROC 曲线
真正率(TPR):正样本中被预测为正样本的概率(True Positive Rate)
假正率(FPR):负样本中被预测为正样本的概率(False Positive Rate),FP / FP + TN
概述:(Receiver Operating Characteristic curve)是一种常用于 评估 分类模型 性能 的可视化工具。ROC曲线以模型的 真正率TPR 为纵轴,假正率FPR 为横轴,它将模型在 不同阈值下的表现以曲线的形式展现出来。
6、AUC 曲线下面积
概述:ROC曲线的优劣可以通过曲线下的面积(AUC)来衡量,AUC越大表示分类器 性能越好
当AUC <= 0.5 时,表示分类器的性能等同于随机猜测
当AUC = 1时,表示分类器的性能完美,能够完全正确地将正负例分类。
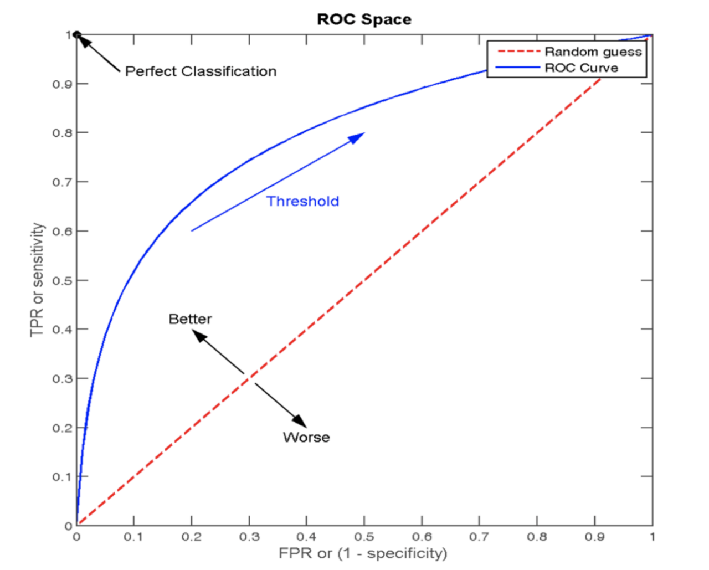
点(0, 0) :所有的负样本都预测正确,所有的正样本都预测错误,相当于点的 (FPR值0, TPR值0)
点(1, 0) :所有的负样本都预测错误,所有的正样本都预测错误。相当于点的 (FPR值1, TPR值0) 即最不好的效果
点(1, 1):所有的负样本都预测错误,所有的正样本都预测正确。相当于点的 (FPR值1,TPR值1)
点(0, 1):所有的负样本都预测正确,所有的正样本都预测正确。相当于点的 (FPR值0,TPR值1) 即最好的效果
API
1.导包:from sklearn.metrics import roc_auc_score
2. 使用:sklearn.metrics.roc_auc_score ( y_true,y_score )
y_true:每个样本的真实类别,必须为0 ( 反例 ),1 ( 正例 )标记
y_score:预测得分,可以是正例的估计概率、置信值或者分类器方法的返回值
from sklearn.metrics import roc_auc_scoresklearn.metrics.roc_auc_score ( y_true,y_score )7、EDA(探索性数据分析)
概述:围绕目标值进行分析,找到和目标值相关性比较强的特征
8、分类评估报告
sklearn.metrics.classification_report ( y_true,y_pred,labels = [ ],target_names = None )
y_true:真实目标值
y_pred:估计器预测目标值
labels:指定类别对应的数字
target_names:目标类别名称
return:每个类别精确率与召回率
sklearn.metrics.classification_report ( y_true,y_pred,labels = [ ],target_names = None ) 样本不均衡问题处理思路:希望 0、1 标签样本占比 1:1,方案:class_weight = ' balanced '
特征编码:处理类别型数据,做 one - hot 编码:churn_pd = pd.get_dummies ( churn_pd )
churn_pd = pd.get_dummies ( churn_pd )模型保存:1. 导包:import joblib
2. 保存: joblib.dump ( estimator,' . / 文件名.pth ' )
import joblibjoblib.dump ( estimator,' . / 文件名.pth ' )