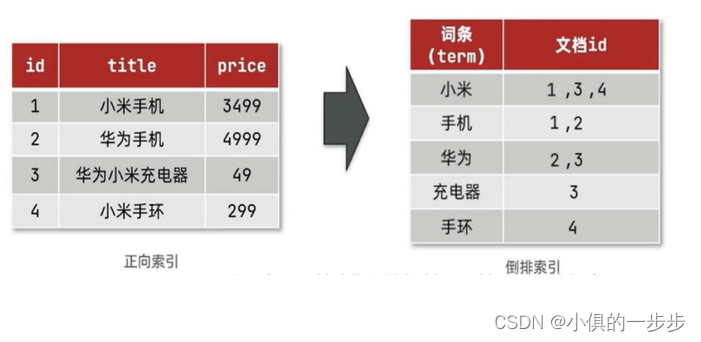
马尔可夫链(Markov Chain)可以说是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测、语音识别方面都有着极其广泛的应用
> The future is independent of the past given the present 未来独立于过去,只基于当下。
这句人生哲理的话也代表了马尔科夫链的思想:过去所有的信息都已经被保存到了现在的状态,基于现在就可以预测未来。
虽然这么说可能有些极端,但是却可以大大简化模型的复杂度,因此马尔可夫链在很多时间序列模型中得到广泛的应用,比如循环神经网络 RNN,隐式马尔可夫模型 HMM 等,当然 MCMC 也需要它。
随机过程
马尔可夫链是随机过程 这门课程中的一部分,先来简单了解一下。
简单来说,随机过程就是使用统计模型一些事物的过程进行预测和处理 ,比如股价预测通过今天股票的涨跌,却预测明天后天股票的涨跌;天气预报通过今天是否下雨,预测明天后天是否下雨。这些过程都是可以通过数学公式进行量化计算的。通过下雨、股票涨跌的概率,用公式就可以推导出来 N 天后的状况。
简介
俄国数学家 Andrey Andreyevich Markov 研究并提出一个用数学方法就能解释自然变化的一般规律模型,被命名为马尔科夫链(Markov Chain)。马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程,该过程要求具备“无记忆性 ”,即下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。
马尔科夫链认为过去所有的信息都被保存在了现在的状态下了 。比如这样一串数列 1 - 2 - 3 - 4 - 5 - 6,在马尔科夫链看来,6 的状态只与 5 有关,与前面的其它过程无关。
数学定义
假设我们的序列状态是,那么在
时刻的状态的条件概率仅依赖于前一刻的状态
即:
既然某一时刻状态转移的概率只依赖于它的前一个状态 ,那么我们只要能求出系统中任意两个状态之间的转换概率,这个马尔科夫链的模型就定了。
转移概率矩阵
通过马尔科夫链的模型转换,我们可以将事件的状态转换成概率矩阵 (又称状态分布矩阵 ),如下例:
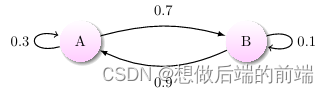
上图中有 A 和 B 两个状态,A 到 A 的概率是 0.3,A 到 B 的概率是 0.7;B 到 B 的概率是 0.1,B 到 A 的概率是 0.9。
初始状态在 A,如果我们求 2 次运动后状态还在 A 的概率是多少?非常简单: P=A→A→A+A→B→A=0.3∗0.3+0.7∗0.9=0.72
如果求 2 次运动后的状态概率分别是多少?初始状态和终止状态未知时怎么办呢?这是就要引入转移概率矩阵 ,可以非常直观的描述所有的概率。
有了状态矩阵,我们可以轻松得出以下结论:
- 初始状态 A,2 次运动后状态为 A 的概率是 0.72;
- 初始状态 A,2 次运动后状态为 B 的概率是 0.28;
- 初始状态 B,2 次运动后状态为 A 的概率是 0.36;
- 初始状态 B,2 次运动后状态为 B 的概率是 0.64;
来看一个多个状态更复杂的情况:

状态转移矩阵的稳定性
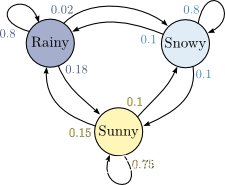
状态转移矩阵有一个非常重要的特性,经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态概率分布无关。例如
假设我们当前股市的概率分布为: [ 0.3 , 0.4 , 0.3 ] [0.3, 0.4, 0.3][0.3,0.4,0.3] ,即 30% 概率的牛市,40% 概率的熊盘与 30% 的横盘。然后这个状态作为序列概率分布的初始状态,将其代入这个状态转移矩阵计算
的状态。代码如下:
matrix = np.matrix([[0.9, 0.075, 0.025],[0.15, 0.8, 0.05],[0.25, 0.25, 0.5]], dtype=float)
vector1 = np.matrix([[0.3, 0.4, 0.3]], dtype=float)for i in range(100):vector1 = vector1 * matrixprint('Courrent round: {}'.format(i+1))print(vector1)
输出结果:
Current round: 1
[[ 0.405 0.4175 0.1775]]
Current round: 2
[[ 0.4715 0.40875 0.11975]]
Current round: 3
[[ 0.5156 0.3923 0.0921]]
Current round: 4
[[ 0.54591 0.375535 0.078555]]
。。。。。。
Current round: 58
[[ 0.62499999 0.31250001 0.0625 ]]
Current round: 59
[[ 0.62499999 0.3125 0.0625 ]]
Current round: 60
[[ 0.625 0.3125 0.0625]]
。。。。。。
Current round: 99
[[ 0.625 0.3125 0.0625]]
Current round: 100
[[ 0.625 0.3125 0.0625]]
可以发现,从第 60 轮开始,我们的状态概率分布就不变了,一直保持[ 0.625 , 0.3125 , 0.0625 ],即 62.5% 的牛市,31.25% 的熊市与 6.25% 的横盘。
这个性质不仅对状态转移矩阵有效,对于绝大多数的其他的马尔可夫链模型的状态转移矩阵也有效。同时不光是离散状态,连续状态时也成立。
马尔科夫链的应用
语言模型
自然语言处理、语音处理中经常用到语言模型, 是建立在词表上的 n nn 阶马尔可夫链。比如, 在英语语音识别中,语音模型产生出两个候选: “How to recognize speech” 与 "How to wreck a nice beach”,语言模型要判断哪个可能性更大
将一个语句看作是一个单词的序列 ,目标是计算其概率。同一个语句很少在语料中重复多次出现,所以直接从语料中估计每个语句的概率是困难的。语言模型用局部的单词序列的概率,组合计算出全局的单词序列的概率,可以很好地解决这个问题。假设每个单词只依赖于其前面出现的单词,也就是说单词序列具有马尔可夫性,那么可以定义一阶马尔可夫链 (可以轻易扩展到 n 阶马尔可夫链),即语言模型,如下计算语句的概率:
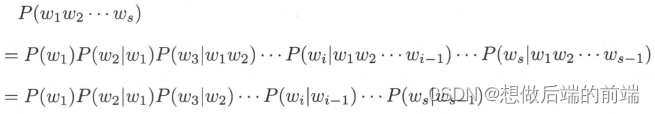
如果有充分的语料,转移概率可以直接从语料中估计。直观上, “wreck a nice” 出现之后,下面出现 “beach” 的概率极低,所以第二个语句的概率应该更小,从语言模型的角度看第一个语句的可能性更大
信号传输
考虑通过电话线或无线电波传输信号的问题。每条数据都必须经过一个多阶段的过程才能传输,并且在每个阶段都存在传输错误导致数据损坏的概率。
假设传输中发生错误的概率不受过去传输错误的影响,不依赖于时间,并且可能的数据条数是有限的。然后可以通过马尔可夫链建模传输过程,状态为0和1以及转移矩阵