617.合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

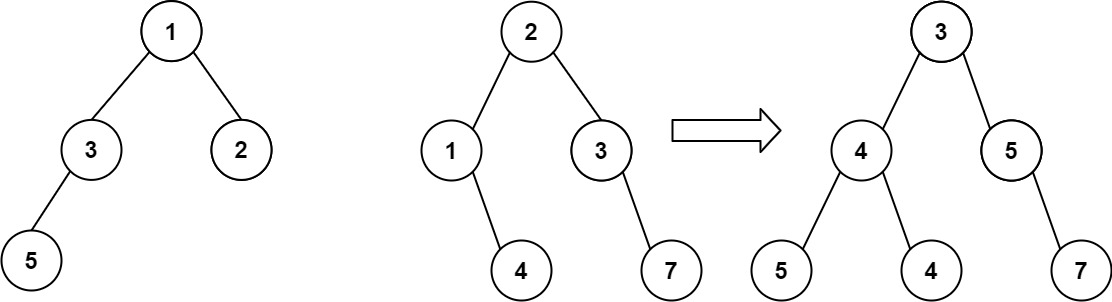
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• -104 <= Node.val <= 104

思路

广度优先搜索

 这题用广搜要用到三个队列，然后层序遍历，每次入队时判断两个节点状态，分为都非空、1空、2空的情况去判断，个人评价是垃圾解法。

class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1==null&&root2==null){return null;}if(root1==null){return root2;}if(root2==null){return root1;}TreeNode merged=new TreeNode(root1.val+root2.val);Queue<TreeNode> queue=new LinkedList<TreeNode>();Queue<TreeNode> queue1=new LinkedList<TreeNode>();Queue<TreeNode> queue2=new LinkedList<TreeNode>();queue.offer(merged);queue1.offer(root1);queue2.offer(root2);while(!queue1.isEmpty()&&!queue2.isEmpty()){TreeNode node=queue.poll(),node1=queue1.poll(),node2=queue2.poll();TreeNode left1=node1.left,left2=node2.left,right1=node1.right,right2=node2.right;if(left1!=null||left2!=null){if(left1!=null&&left2!=null){TreeNode left=new TreeNode(left1.val+left2.val);node.left=left;queue.offer(left);queue1.offer(left1);queue2.offer(left2);} else if(left1!=null){node.left=left1;} else if (left2 != null) {node.left=left2;}}if(right1!=null||right2!=null){if(right1!=null&&right2!=null){TreeNode right=new TreeNode(right1.val+right2.val);node.right=right;queue.offer(right);queue1.offer(right1);queue2.offer(right2);} else if(right1!=null){node.right=right1;} else if (right2 != null) {node.right=right2;}}}return merged;}
}

搞这么长有什么意义吗？

深度优先搜索

class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1==null){return root2;}if(root2==null){return root1;}TreeNode emerged=new TreeNode(root1.val+root2.val);emerged.left=mergeTrees(root1.left,root2.left);emerged.right=mergeTrees(root1.right,root2.right);return emerged;}
}

直接贴代码，赏心悦目。

首先看是否有空树，有的话直接返回另一棵。

判断完之后两树均非空，则新增一个两树当前节点值之和的节点代替当前节点，之后往该节点的左右子树继续递归。

总结

深搜还有一种解法好像可以在树1上直接操作，看起来会更省空间一点，可以再考虑一下。