蓝桥杯备赛 day 3 —— 高精度（C/C++，零基础，配图）

🌈前言：

📁 高精度的概念

📁 高精度加法和其模板

📁 高精度减法和其模板

📁 高精度乘法和其模板

📁 高精度除法和其模板

📁 总结

🌈前言：

这篇文章主要是准备蓝桥杯竞赛同学所写，为你更好准备蓝桥杯比赛涉及的算法知识点。不知道你是否苦恼于不知算法从何学起，苦恼于网上资料稀少，或者复杂难懂，这篇文章就是帮助这部分同学的。

下面整理了蓝桥杯考点大纲：
蓝桥杯考点大纲

如果你对vecto数组r有兴趣，也可以阅读下面这篇文章，当然没了解vector数组也不影响阅读本篇文章

和C++STL中vector的初次见面，vector常见用法和操作（零基础/小白）-CSDN博客

上图是大学C组需要掌握的，对于B组的同学也是需要向下掌握的。本文主要是帮助蓝桥杯B/C为主体的大部分同学，所以讲解相对基础。本文是以C++为主要语言，但是C语言的同学也不需要担心，大部分语法是相通的，只不过是加了STL内容一个内容，也是会进行讲解的。

因为语法特性，变量等原因，对于JAVA，Python同学来说是不需要掌握高精度的。

同时本文将提供做题模板，方便你在考试中更好的做题，以及日常的刷题。

📁 高精度的概念

我们用C/C++创建变量时，变量类型是有取值范围的，对于最常用unsigned int来说，它最多有-2147483648 ~ 2147483647,即-(2^31)~(2^31-1），也就是说最多有31位, 那我们想存长度为10^6的数呢，这是我们就不能用C/C++语法规定的变量来存储了，我们就必须用数组来存储。

总结一下，高精度就是通过数组模拟四则运算来计算长度非常长的数字。

本文只讲解比较常见的四种高精度算法，如两个高精度数相加，两个高精度数相间，高精度数乘低精度数，高精度数除以低精度数。

通常来说，高精度灰常大，如10^6，低精度数10000以内。

对于高精度数这么多位数来说，我们首先想到的是整数数组来存储，可是有一个问题是存储呢是从后往前存储，还是从前往后存储？比如123，下标0是在1的位置，还是3的位置呢？

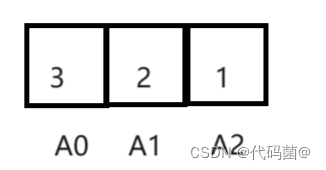
如果从1开始那么计算是否方便，很显然这是不方便的，如果感兴趣，可以自己尝试一下。可是对于从3开始存储，一开始我们怎么会知道他有多少位数呢？相信你一定知道数组还有一种叫做字符数组的，我们可以先将字符数字存储在字符数组中，再将字符数字逆序存储成整数数组中进行计算，这样大大减少了运算时进位的难度。（数组从前往后遍历如果遇到进位时，只需要下一个位置的数+1即可）

📁 高精度加法和其模板

我们首先来看一下，普通的加法怎么计算。

加法运算就是从个位开始相加，相加大于10就向前进1位，即向前一位+1。前面我们说了，高精度是通过数组来模拟计算的，如下图所示。

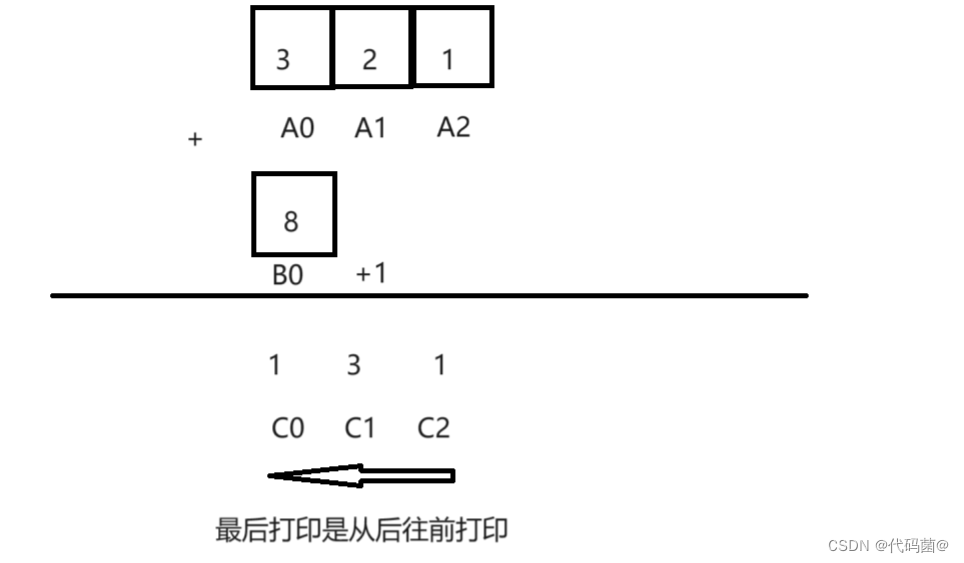
通过上图我们就可以得出模板：

vector<int> add(vector<int> A,vector<int> B)
{vector<int> C;int t = 0;    //t是进位for(int i=0;i<A.size() || i < B.size();i++{if(i < A.size())t += A[i];if(i < B.size())t += B[i];C.push_back(t % 10);t /= 10;}if(t)C.push_back(t);return C;}

这里为了更好照顾C语言同学，讲解一下什么是vector<int> , 可以理解为数组，每个元素类型是int，即整数数组。

.size()可以理解为对数组的操作，求数组元素个数；.push_back()也是同理，向数组C插入元素的。

整体通读一遍模板代码，先创建数组C存储结果，当然是从个位先开始存储的。t是进位，如果Ai，Bi在i位置上有数，就加到t中，t就是相加结果，如果大于10，保留个位数，向前+1，t%10。

最后判断最大位数相加是否向前进1位，就是判断t，这里t只能取到0或者1。

以上，我们就对高精度加法模板有了了解，下面我们展示完整代码：

#include <iostream>
#include <vector>using namespace std;vector<int> add(vector<int> A, vector<int> B)
{vector<int> C;int t = 0;		//进位for (int i = 0;i < A.size() || i < B.size();i++){if (i < A.size())t += A[i];if(i < B.size())t += B[i];C.push_back(t % 10);t /= 10;}if (t)C.push_back(t);return C;
}int main()
{string a, b;cin >> a >> b;vector<int> A, B;for (int i = a.size() - 1;i >= 0;i--) A.push_back(a[i] - '0');            //将 字符数字 -> 整数数字for (int i = b.size() - 1;i >= 0;i--)B.push_back(b[i] - '0');vector<int> C = add(A, B);for (int i = C.size() - 1;i >= 0;i--)cout << C[i];return 0;
}

如果我们要使用vector数组的话，要引用头文件。

📁 高精度减法和其模板

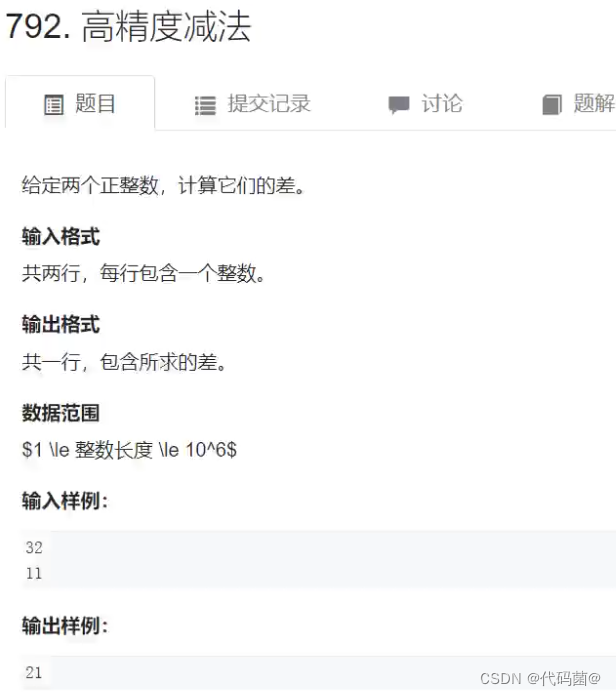
A-B，我们要分两种情况，即A>=B,和 A < B；对于第1种情况，我们直接输出A-B即可，对于第二种情况我们输出 - (B - A);

对于模板，我们只需要确保A>=B即可。

vector<int> sub(vector<int> A,vector<int> B)
{vector<int> C;int t = 0;        //借位for(int i=0;i<A.size();i++){t = A[i] + t;if(i < B[i])t -= B[i];C.push_back((t + 10) % 10);if(t < 0)t = -1;elset = 0;    }while(C.size() > 1 && C.back() == 0)C.pop_back();return C;
}

(t+10)%10,是为了保证减不开的情况，对于相减大于0的数不影响。

最后的while循环是为了保证一种情况，例如，127-120，在数组C中存储的是300,最后打印007了，所以我们要将前面两个0删去，当然如果是127-127，是要保留1个0的。

下面展示完整代码：

当然，我们下面还写了一个函数check，作用就是判断A是否大于等于B的。

#include <iostream>
#include <vector>using namespace std;bool check(vector<int> A, vector<int> B)
{if (A.size() > B.size())return true;for (int i = 0;i < A.size();i++)if (A[i] != B[i])return A[i] > B[i];return true;
}vector<int> sub(vector<int> A, vector<int> B)
{vector<int>	C;int t = 0;for (int i = 0;i < A.size();i++){t = A[i] + t;if (i < B.size())t -= B[i];C.push_back((t + 10) % 10);if (t < 0)t = -1;elset = 0;}while (C.size() > 1 && C.back() == 0)C.pop_back();return C;
}int main()
{string a, b;cin >> a >> b;vector<int> A, B;for (int i = a.size() - 1;i >= 0;i--)A.push_back(a[i] - '0');for (int i = b.size() - 1;i >= 0;i--)B.push_back(b[i] - '0');if (check(A, B)){vector<int> C = sub(A, B);for (int i = C.size() - 1;i >= 0;i--)cout << C[i];}else{vector<int> C = sub(B, A);cout << '-';for (int i = C.size() - 1;i >= 0;i--)cout << C[i];}return 0;
}

📁 高精度乘法和其模板

下图便是高精度与低精度整数想乘的运算方式，将每一位数乘低精度数b + 上一位的进位，余数就是这位上的数，进位等于相除的结果。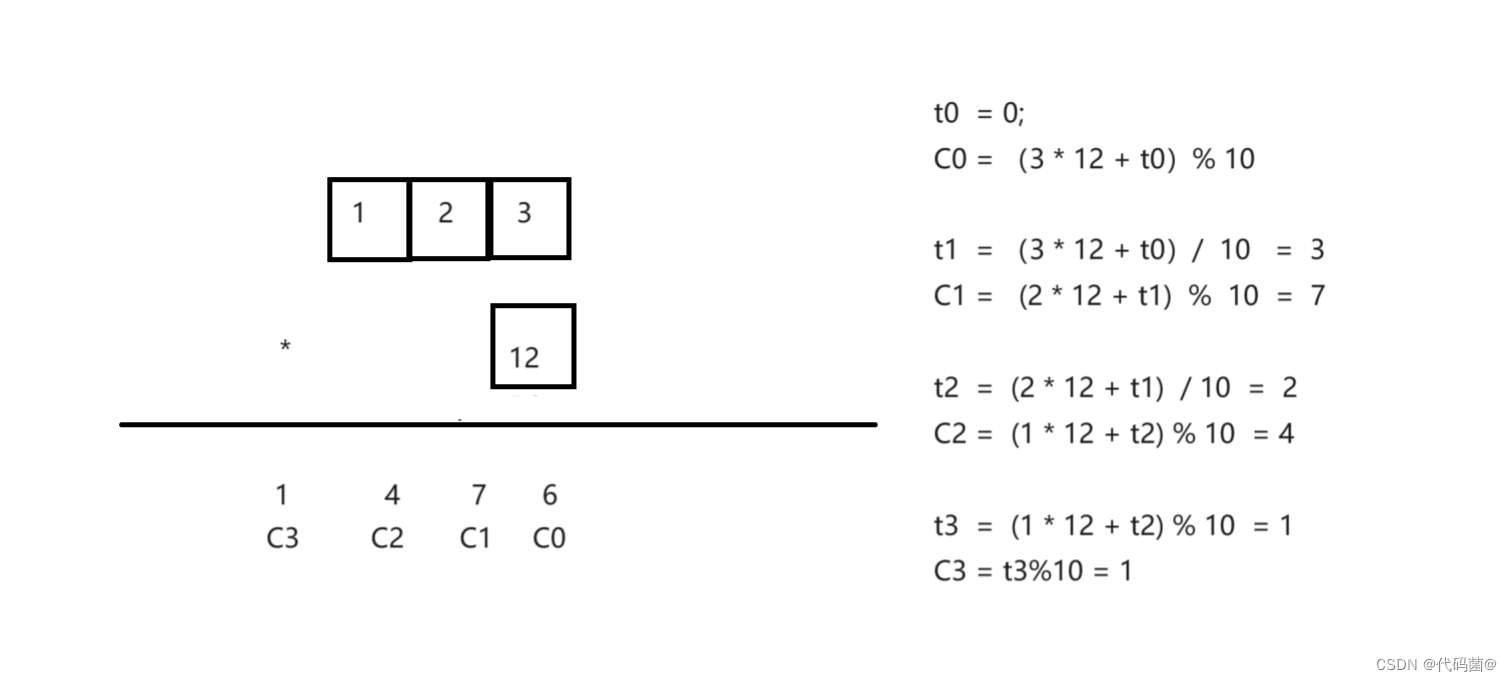

得出模板为：

vector<int> mul(vector<int> A, int b)
{vector<int> C;int t = 0;for (int i = A.size() - 1;i >= 0 || t; i--){if(i < A.size())t += A[i] * b;C.push_back(t % 10);t /= 10;}while (C.size() > 1 && C.back() == 0)C.pop_back();return C;
}

当然最后还是要保证A*0的话只能有1个0。

下面展示完整代码：

#include <iostream>
#include <vector>using namespace std;vector<int> mul(vector<int> A, int b)
{vector<int> C;int t = 0;for (int i = A.size() - 1;i >= 0 || t; i--){if(i < A.size())t += A[i] * b;C.push_back(t % 10);t /= 10;}while (C.size() > 1 && C.back() == 0)C.pop_back();return C;
}int main()
{string a;cin >> a;int b;cin >> b;vector<int> A;for (int i = a.size() - 1;i >= 0;i--)A.push_back(a[i] - '0');vector<int> C = mul(A, b);for (int i = C.size() - 1;i >= 0;i--)cout << C[i];return 0;
}

📁 高精度除法和其模板

除法相对于上面三个有点不同，高精度数A是从最高位开始计算的，我们数组C存储也是从最高位开始存储，但是我们为了和上面保持一致，即输出都是从后往前输出，所以我们最后逆置数组。

这里为什么从0开始计算呢，是从1开始计算的，上一位的补下来是0，所以1/3=1，余数是1,，依次类推。理解了这里，高精度除法也就懂了。

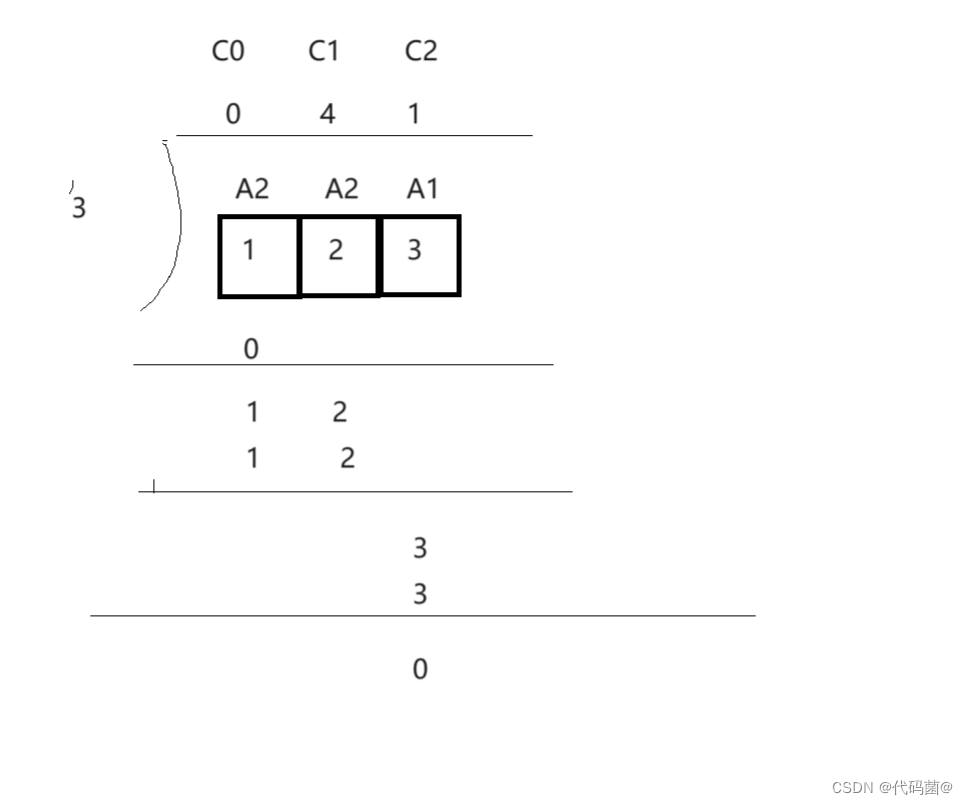
下面展示模板：

vector<int> div(vector<int> A, int b, int& r)
{vector<int> C;for (int i = A.size()-1;i >=0;i--){r = r * 10 + A[i];C.push_back(r / b);r %= b;}reverse(C.begin(),C.end());while (C.size() > 1 && C.back() == 0)C.pop_back();return C;
}

reverse()函数就是将数组元素逆置，其中begin(),end()你可以先简单理解为首元素位置，尾元素位置，将这两个参数传给reverse函数。函数是包含在头文件<algorithm>中

下面展示完整代码：

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;vector<int> div(vector<int> A, int b, int& r)
{vector<int> C;for (int i = A.size()-1;i >=0;i--){r = r * 10 + A[i];C.push_back(r / b);r %= b;}reverse(C.begin(),C.end());while (C.size() > 1 && C.back() == 0)C.pop_back();return C;
}int main()
{string a;cin >> a;int b;cin >> b;vector<int> A;for (int i = a.size() - 1;i >= 0;i--)A.push_back(a[i] - '0');int r = 0;vector<int> C = div(A,b,r);for (int i = C.size() - 1;i >= 0;i--)cout << C[i];cout << endl << r << endl;return 0;
}