本节内容:二进制
■电子计算机为何采用二进制:电子计算机电路只有低电平和高电平两种状态,分别表示二进制数0和1。
■二进制的简写形式:计算机内的数据都使用二进制数。但是二进制书写不便,通常我们采用十六进制作为二进制的简写形式来表示二进制数。
■进制间的转换:4位二进制数表示为1位十六进制数0~F。4位二进制数表示1位十进制数0~9。二进制数或十六进制数转换为十进制数采用位权法。十进制数转换为二进制数或十六进制数采用除法。
2.3.1 电子计算机为何采用二进制
我们可能会有这样的想法,如果电子计算机刚发明的时候采用十进制就好了,用不着来回转换,而且我们也非常熟悉十进制。
也有人会说二进制如何好,简单高效。其实这种说法是错误的。十进制的算术逻辑运算要比二进制的效率高的多。毕竟计算的步骤少了很多。
其实真正采用二进制的原因是由于电子计算机受制于计算机物理硬件的制约。电子计算机电路只有0和1两种稳定的状态,二进制才是电子计算机最合理的选择。况且二进制算术逻辑运算和十进制算术逻辑运算是一样的,并不影响计算结果的正确性,只是二进制算术逻辑运算的效率比十进制低。由于电子计算机的运算速度足够快,可以弥补效率低的缺陷。因此,计算机中存储的任何数据和指令都是由二进制数0和1组成的。
其实电子计算机的理论基础早在一百多年以前就已经完成了,只是受制于当时的材料和工艺的制约。当电子管、集成电路发明出来之后,有了合适的材料,电子计算机自然也就发明出来了。
量子计算机肯定不再采用二进制,因为量子特性可以同时具备很多种状态,量子计算机的效率肯定比只有0和1的二进制高的多。只是目前量子计算机仍然受制于制造工艺、材料和成本的制约,这些问题一旦得到解决,量子计算机的普及和应用肯定可以飞速实现。
2.3.2 二进制的简写形式
使用4位二进制数书写十进制数0~15:
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
二进制数书写比较麻烦,可以采用二进制的简写形式,即十六进制表示。
使用十六进制数书写十进制数0~15:
0 1 2 3 4 5 6 7 8 9 A B C D E F。
显然十六进制数书写更为简单高效。在以后学习过程中,我们经常使用的工具软件如调试器、编译器、内存分析工具、二进制文本工具等都是使用十六进制来表示二进制数。
2.3.3 进制间的转换
■二进制与十六进制之间的转换
表2-1 二进制与十六进制之间的转换

表2-1 二进制与十六进制之间的转换
■二进制与十进制之间的转换

表2-2 二进制与十进制之间的转换
如表2-1、表2-2所示:每一位十进制数或者十六进制数,分别对应4位二进制数。
十进制数0~9对应的4位二进制数,称为8421 BCD码,我们将在第四章常用编码规则中详细讲解BCD码。
■二进制数转十进制数
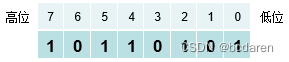
表2-3 二进制数
将上述二进制数转换为对应的十进制数。
算法:位权表示法把n位二进制整数转换为十进制数(不考虑正负数)。
dec=(DN-1×2N-1)+(DN-2×2N-2)+...+(D1×21)+(D0×20) 注:公式中的N代表二进制数位数,
10110101B=1*27+0*26+1*25+1*24+0*23+1*22+0*21+1*20=128+32+16+4+1=181D(D表示十进制),可以使用查表的方法获取2的幂。
| 2n | 十进制值 | 2n | 十进制值 |
| 20 | 1 | 28 | 256 |
| 21 | 2 | 29 | 512 |
| 22 | 4 | 210 | 1024 |
| 23 | 8 | 211 | 2048 |
| 24 | 16 | 212 | 4096 |
| 25 | 32 | 213 | 8192 |
| 26 | 64 | 214 | 16384 |
| 27 | 128 | 215 | 32768 |
表2-4 2进制位的位权值
■十进制数转二进制数
算法:十进制数重复除以2,每次的余数记录下来作为当前二进制数位的值,直到
商为0为止。举例:十进制数57转为二进制数 。
| 除法 | 商 | 余数 |
| 57/2 | 28 | 1 |
| 28/2 | 14 | 0 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1 |
表2-5 十进制数转二进制数除法表
把余数列数字反向排列就得到了二进制数111001,由于intel存储的二进制数位数总是8或者8的倍数,因此前面空位补0,57的二进制数为0011 1001B。
■十六进制数转十进制数
| 16进制数高位 | 1 | 6 | A | 7 | 9 | 4 | 16进制数低位 | ||
| 0001 | 0110 | 1010 | 0111 | 1001 | 0100 | ||||
表2-6 十六进制数转二进制数
算法:位权表示法把n位无符号数十六进制整数转换为十进制数(不考虑正负数),
dec=(DN-1×16N-1)+(DN-2×16N-2)+...+(D1×161)+(D0×160)公式中的N代表十六进制数数位,
16A794H=1*165+6*164+10*163+7*162+9*161+4*160=1484692。
| 16n | 十进制值 | 16n | 十进制值 |
| 160 | 1 | 164 | 65536 |
| 161 | 16 | 165 | 1048576 |
| 162 | 256 | 166 | 16777216 |
| 163 | 4096 | 167 | 268435456 |
表2-7 十六进制位的位权值
■十进制数转十六进制数
算法:
十进制数重复除以16,每次的余数记录下来作为当前十六进制数位的值,直到
商为0为止。举例:十进制数422转为十六进制数。
| 除法 | 商 | 余数 |
| 422/16 | 26 | 6 |
| 26/16 | 1 | A |
| 1/16 | 0 | 1 |
表2-8 十进制数转十六进制数除法
把余数列数字反向排列就得到了十六进制数1A6H,由于intel存储的二进制数位数总是8或者8的倍数,因此前面空位补0,422的十六进制数为01A6H。
练习
1、将下面的二进制数用16进制表示(不允许使用计算器也不允许计算)
1100 1011 0101 0100 1110 1011 0101 0111 1011 0100 1010 1011。
2、将下面的十六进制数用二进制表示(不允许使用计算器也不允许计算)
487FDC120ACE69B953FE。
3、将下面的二进制数转换为十进制正整数(先使用算法,然后用计算器检验)。
00100111B 101101101111B 01100001B
4、将下面的十进制正整数转换为二进制数(先使用算法,然后用计算器检验)。
121D 2345D 13124D 121798D
5、将下面的16进制正整数数转换为十进制数(先使用算法,然后用计算器检验)。
87DAFH 875B3FH 7A8CBFFH 1234H
6、将下面的十进制正整数数转换为十六进制数(先使用算法,然后用计算器检验)。
412434D 3643D 643262D 345D
本文摘自编程达人系列教材《X86汇编语言基础教程》。