🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/literature?__c=1000,移动端可微信小程序搜索“历代文学”)总架构师,
15年工作经验,精通Java编程,高并发设计,Springboot和微服务,熟悉Linux,ESXI虚拟化以及云原生Docker和K8s,热衷于探索科技的边界,并将理论知识转化为实际应用。保持对新技术的好奇心,乐于分享所学,希望通过我的实践经历和见解,启发他人的创新思维。在这里,我希望能与志同道合的朋友交流探讨,共同进步,一起在技术的世界里不断学习成长。
技术合作请加本人wx(注明来自csdn):foreast_sea


Java 基础面试题
- Java 基础面试题
- Java 基础篇
- Java 有哪些特点
- Java 的特性
- 描述一下值传递和引用传递的区别
- == 和 equals 区别是什么
- String 中的 equals 是如何重写的
- 为什么重写 equals 方法必须重写 hashcode 方法
- String s1 = new String(“abc”) 在内存中创建了几个对象
- String 为什么是不可变的、jdk 源码中的 String 如何定义的、为什么这么设计。
- static 关键字是干什么用的?谈谈你的理解
- final 关键字是干什么用的?谈谈你的理解
- 抽象类和接口的区别是什么
- 重写和重载的区别
- byte的取值范围是多少,怎么计算出来的
- HashMap 和 HashTable 的区别
- HashMap 和 HashSet 的区别
- HashMap 的底层结构
- HashMap 的长度为什么是 2 的幂次方
- HashMap 多线程操作导致死循环问题
- HashMap 线程安全的实现有哪些
- 讲一下 HashMap put 的过程
- ConcurrentHashMap 底层实现
- Integer 缓存池
- UTF-8 和 Unicode 的关系
- 项目为 UTF-8 环境,char c = ‘中’,是否合法
- Arrays.asList 获得的 List 应该注意什么
- Collection 和 Collections 的区别
- 你知道 fail-fast 和 fail-safe 吗
- ArrayList、LinkedList 和 Vector 的区别
- Exception 和 Error 有什么区别
- String、StringBuilder 和 StringBuffer 有什么区别
- 动态代理是基于什么原理
- int 和 Integer 的区别
- Java 提供了哪些 I/O 方式
- 谈谈你知道的设计模式
- Comparator 和 Comparable 有什么不同
- Object 类中一般都有哪些方法
- Java 泛型和类型擦除
- 反射的基本原理,反射创建类实例的三种方式是什么
- 强引用、若引用、虚引用和幻象引用的区别
- final、finally 和 finalize() 的区别
- 内部类有哪些分类,分别解释一下
- 说出几种常用的异常
- 静态绑定和动态绑定的区别
- 绑定
- 静态绑定
- 动态绑定
- 动态绑定和静态绑定的特点
- Java 有哪些特点
- Java 基础篇
Java 基础篇
Java 有哪些特点
并发性的: 你可以在其中执行许多语句,而不必一次执行它面向对象的:基于类和面向对象的编程语言。独立性的: 支持一次编写,到处运行的独立编程语言,即编译后的代码可以在支持 Java 的所有平台上运行。
Java 的特性
Java 的特性有如下这几点
-
简单,Java 会让你的工作变得更加轻松,使你把关注点放在主要业务逻辑上,而不必关心指针、运算符重载、内存回收等与主要业务无关的功能。 -
便携性,Java 是平台无关性的,这意味着在一个平台上编写的任何应用程序都可以轻松移植到另一个平台上。 -
安全性, 编译后会将所有的代码转换为字节码,人类无法读取。它使开发无病毒,无篡改的系统/应用成为可能。 -
动态性,它具有适应不断变化的环境的能力,它能够支持动态内存分配,从而减少了内存浪费,提高了应用程序的性能。 -
分布式,Java 提供的功能有助于创建分布式应用。使用远程方法调用(RMI),程序可以通过网络调用另一个程序的方法并获取输出。您可以通过从互联网上的任何计算机上调用方法来访问文件。这是革命性的一个特点,对于当今的互联网来说太重要了。 -
健壮性,Java 有强大的内存管理功能,在编译和运行时检查代码,它有助于消除错误。 -
高性能,Java 最黑的科技就是字节码编程,Java 代码编译成的字节码可以轻松转换为本地机器代码。通过 JIT 即时编译器来实现高性能。 -
解释性,Java 被编译成字节码,由 Java 运行时环境解释。 -
多线程性,Java支持多个执行线程(也称为轻量级进程),包括一组同步原语。这使得使用线程编程更加容易,Java 通过管程模型来实现线程安全性。
描述一下值传递和引用传递的区别
要想真正理解的话,可以参考这篇文章 : https://www.zhihu.com/question/31203609
简单理解的话就是
值传递是指在调用函数时将实际参数复制一份到函数中,这样的话如果函数对其传递过来的形式参数进行修改,将不会影响到实际参数
引用传递 是指在调用函数时将对象的地址直接传递到函数中,如果在对形式参数进行修改,将影响到实际参数的值。
== 和 equals 区别是什么
== 是 Java 中一种操作符,它有两种比较方式
- 对于
基本数据类型来说, == 判断的是两边的值是否相等
public class DoubleCompareAndEquals {Person person1 = new Person(24,"boy");Person person2 = new Person(24,"girl");int c = 10;private void doubleCompare(){int a = 10;int b = 10;System.out.println(a == b);System.out.println(a == c);System.out.println(person1.getId() == person2.getId());}
}
- 对于
引用类型来说, == 判断的是两边的引用是否相等,也就是判断两个对象是否指向了同一块内存区域。
private void equals(){System.out.println(person1.getName().equals(person2.getName()));
}
equals 是 Java 中所有对象的父类,即 Object 类定义的一个方法。它只能比较对象,它表示的是引用双方的值是否相等。所以记住,并不是说 == 比较的就是引用是否相等,equals 比较的就是值,这需要区分来说的。
equals 用作对象之间的比较具有如下特性
自反性:对于任何非空引用 x 来说,x.equals(x) 应该返回 true。对称性:对于任何非空引用 x 和 y 来说,若x.equals(y)为 true,则y.equals(x)也为 true。传递性:对于任何非空引用的值来说,有三个值,x、y 和 z,如果x.equals(y) 返回true,y.equals(z) 返回true,那么x.equals(z) 也应该返回true。一致性:对于任何非空引用 x 和 y 来说,如果 x.equals(y) 相等的话,那么它们必须始终相等。非空性:对于任何非空引用的值 x 来说,x.equals(null) 必须返回 false。
String 中的 equals 是如何重写的
String 代表的是 Java 中的字符串,String 类比较特殊,它整个类都是被 final 修饰的,也就是说,String 不能被任何类继承,任何 修改 String 字符串的方法都是创建了一个新的字符串。
equals 方法是 Object 类定义的方法,Object 是所有类的父类,当然也包括 String,String 重写了 equals 方法,下面我们来看看是怎么重写的

- 首先会判断要比较的两个字符串它们的
引用是否相等。如果引用相等的话,直接返回 true ,不相等的话继续下面的判断 - 然后再判断被比较的对象是否是 String 的实例,如果不是的话直接返回 false,如果是的话,再比较两个字符串的长度是否相等,如果长度不想等的话也就没有比较的必要了;长度如果相同,会比较字符串中的每个
字符是否相等,一旦有一个字符不相等,就会直接返回 false。
下面是它的流程图

这里再提示一下,你可能有疑惑什么时候是
if (this == anObject) {return true;
}
这个判断语句如何才能返回 true?因为都是字符串啊,字符串比较的不都是堆空间吗,猛然一看发现好像永远也不会走,但是你忘记了 String.intern() 方法,它表示的概念在不同的 JDK 版本有不同的区分
在 JDK1.7 及以后调用 intern 方法是判断运行时常量池中是否有指定的字符串,如果没有的话,就把字符串添加到常量池中,并返回常量池中的对象。
验证过程如下
private void StringOverrideEquals(){String s1 = "aaa";String s2 = "aa" + new String("a");String s3 = new String("aaa");System.out.println(s1.intern().equals(s1));System.out.println(s1.intern().equals(s2));System.out.println(s3.intern().equals(s1));}
-
首先 s1.intern.equals(s1) 这个无论如何都返回 true,因为 s1 字符串创建出来就已经在常量池中存在了。
-
然后第二条语句返回 false,因为 s1 返回的是常量池中的对象,而 s2 返回的是堆中的对象
-
第三条语句 s3.intern.equals(s1),返回 true ,因为 s3 对象虽然在堆中创建了一个对象,但是 s3 中的 “aaa” 返回的是常量池中的对象。

为什么重写 equals 方法必须重写 hashcode 方法
equals 方法和 hashCode 都是 Object 中定义的方法,它们经常被一起重写。
equals 方法是用来比较对象大小是否相等的方法,hashcode 方法是用来判断每个对象 hash 值的一种方法。如果只重写 equals 方法而不重写 hashcode 方法,很可能会造成两个不同的对象,它们的 hashcode 也相等,造成冲突。比如
String str1 = "通话";
String str2 = "重地";
它们两个的 hashcode 相等,但是 equals 可不相等。
我们来看一下 hashCode 官方的定义

总结起来就是
- 如果在 Java 运行期间对同一个对象调用 hashCode 方法后,无论调用多少次,都应该返回相同的 hashCode,但是在不同的 Java 程序中,执行 hashCode 方法返回的值可能不一致。
- 如果两个对象的 equals 相等,那么 hashCode 必须相同
- 如果两个对象 equals 不相等,那么 hashCode 也有可能相同,所以需要重写 hashCode 方法,因为你不知道 hashCode 的底层构造(反正我是不知道,有大牛可以传授传授),所以你需要重写 hashCode 方法,来为不同的对象生成不同的 hashCode 值,这样能够提高不同对象的访问速度。
- hashCode 通常是将地址转换为整数来实现的。
String s1 = new String(“abc”) 在内存中创建了几个对象
一个或者两个,String s1 是声明了一个 String 类型的 s1 变量,它不是对象。使用 new 关键字会在堆中创建一个对象,另外一个对象是 abc ,它会在常量池中创建,所以一共创建了两个对象;如果 abc 在常量池中已经存在的话,那么就会创建一个对象。
详细请翻阅笔者的另外一篇文章 一篇与众不同的 String、StringBuffer、StringBuilder 详解
String 为什么是不可变的、jdk 源码中的 String 如何定义的、为什么这么设计。
首先了解一下什么是不可变对象,不可变对象就是一经创建后,其对象的内部状态不能被修改,啥意思呢?也就是说不可变对象需要遵守下面几条原则
- 不可变对象的内部属性都是 final 的
- 不可变对象的内部属性都是 private 的
- 不可变对象不能提供任何可以修改内部状态的方法、setter 方法也不行
- 不可变对象不能被继承和扩展
与其说问 String 为什么是不可变的,不如说如何把 String 设计成不可变的。
String 类是一种对象,它是独立于 Java 基本数据类型而存在的,String 你可以把它理解为字符串的集合,String 被设计为 final 的,表示 String 对象一经创建后,它的值就不能再被修改,任何对 String 值进行修改的方法就是重新创建一个字符串。String 对象创建后会存在于运行时常量池中,运行时常量池是属于方法区的一部分,JDK1.7 后把它移到了堆中。
不可变对象不是真的不可变,可以通过反射来对其内部的属性和值进行修改,不过一般我们不这样做。
static 关键字是干什么用的?谈谈你的理解
static 是 Java 中非常重要的关键字,static 表示的概念是 静态的,在 Java 中,static 主要用来
- 修饰变量,static 修饰的变量称为
静态变量、也称为类变量,类变量属于类所有,对于不同的类来说,static 变量只有一份,static 修饰的变量位于方法区中;static 修饰的变量能够直接通过 类名.变量名 来进行访问,不用通过实例化类再进行使用。 - 修饰方法,static 修饰的方法被称为
静态方法,静态方法能够直接通过 类名.方法名 来使用,在静态方法内部不能使用非静态属性和方法 - static 可以修饰代码块,主要分为两种,一种直接定义在类中,使用
static{},这种被称为静态代码块,一种是在类中定义静态内部类,使用static class xxx来进行定义。 - static 可以用于静态导包,通过使用
import static xxx来实现,这种方式一般不推荐使用 - static 可以和单例模式一起使用,通过双重检查锁来实现线程安全的单例模式。
final 关键字是干什么用的?谈谈你的理解
final 是 Java 中的关键字,它表示的意思是 不可变的,在 Java 中,final 主要用来
- 修饰类,final 修饰的类不能被继承,不能被继承的意思就是不能使用
extends来继承被 final 修饰的类。 - 修饰变量,final 修饰的变量不能被改写,不能被改写的意思有两种,对于基本数据类型来说,final 修饰的变量,其值不能被改变,final 修饰的对象,对象的引用不能被改变,但是对象内部的属性可以被修改。final 修饰的变量在某种程度上起到了
不可变的效果,所以,可以用来保护只读数据,尤其是在并发编程中,因为明确的不能再为 final 变量进行赋值,有利于减少额外的同步开销。 - 修饰方法,final 修饰的方法不能被重写。
- final 修饰符和 Java 程序性能优化没有必然联系
抽象类和接口的区别是什么
抽象类和接口都是 Java 中的关键字,抽象类和接口中都允许进行方法的定义,而不用具体的方法实现。抽象类和接口都允许被继承,它们广泛的应用于 JDK 和框架的源码中,来实现多态和不同的设计模式。
不同点在于
抽象级别不同:类、抽象类、接口其实是三种不同的抽象级别,抽象程度依次是 接口 > 抽象类 > 类。在接口中,只允许进行方法的定义,不允许有方法的实现,抽象类中可以进行方法的定义和实现;而类中只允许进行方法的实现,我说的方法的定义是不允许在方法后面出现{}使用的关键字不同:类使用class来表示;抽象类使用abstract class来表示;接口使用interface来表示变量:接口中定义的变量只能是公共的静态常量,抽象类中的变量是普通变量。
重写和重载的区别
在 Java 中,重写和重载都是对同一方法的不同表现形式,下面我们针对重写和重载做一下简单的区分
子父级关系不同,重写是针对子级和父级的不同表现形式,而重载是在同一类中的不同表现形式;概念不同,子类重写父类的方法一般使用@override来表示;重写后的方法其方法的声明和参数类型、顺序必须要与父类完全一致;重载是针对同一类中概念,它要求重载的方法必须满足下面任何一个要求:方法参数的顺序,参数的个数,参数的类型任意一个保持不同即可。
byte的取值范围是多少,怎么计算出来的
byte 的取值范围是 -128 -> 127 之间,一共是 256 位。一个 byte 类型在计算机中占据一个字节,那么就是 8 bit,所以最大就是 2^7 = 1111 1111。
Java 中用补码来表示二进制数,补码的最高位是符号位,最高位用 0 表示正数,最高位 1 表示负数,正数的补码就是其本身,由于最高位是符号位,所以正数表示的就是 0111 1111 ,也就是 127。最大负数就是 1111 1111,这其中会涉及到两个 0 ,一个 +0 ,一个 -0 ,+0 归为正数,也就是 0 ,-0 归为负数,也就是 -128,所以 byte 的范围就是 -128 - 127。
HashMap 和 HashTable 的区别
相同点
HashMap 和 HashTable 都是基于哈希表实现的,其内部每个元素都是 key-value 键值对,HashMap 和 HashTable 都实现了 Map、Cloneable、Serializable 接口。
不同点
-
父类不同:HashMap 继承了
AbstractMap类,而 HashTable 继承了Dictionary类

-
空值不同:HashMap 允许空的 key 和 value 值,HashTable 不允许空的 key 和 value 值。HashMap 会把 Null key 当做普通的 key 对待。不允许 null key 重复。
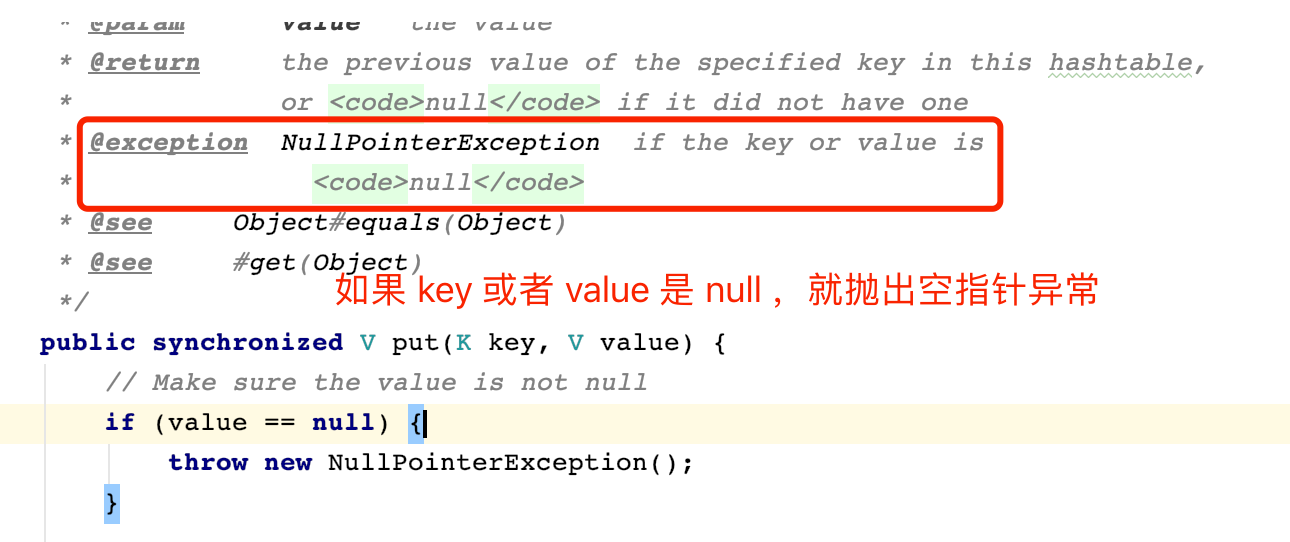
- 线程安全性:HashMap 不是线程安全的,如果多个外部操作同时修改 HashMap 的数据结构比如 add 或者是 delete,必须进行同步操作,仅仅对 key 或者 value 的修改不是改变数据结构的操作。可以选择构造线程安全的 Map 比如
Collections.synchronizedMap或者是ConcurrentHashMap。而 HashTable 本身就是线程安全的容器。 - 性能方面:虽然 HashMap 和 HashTable 都是基于
单链表的,但是 HashMap 进行 put 或者 get 操作,可以达到常数时间的性能;而 HashTable 的 put 和 get 操作都是加了synchronized锁的,所以效率很差。

- 初始容量不同:HashTable 的初始长度是11,之后每次扩充容量变为之前的 2n+1(n为上一次的长度)而 HashMap 的初始长度为16,之后每次扩充变为原来的两倍。创建时,如果给定了容量初始值,那么HashTable 会直接使用你给定的大小,而 HashMap 会将其扩充为2的幂次方大小。
HashMap 和 HashSet 的区别
HashSet 继承于 AbstractSet 接口,实现了 Set、Cloneable,、java.io.Serializable 接口。HashSet 不允许集合中出现重复的值。HashSet 底层其实就是 HashMap,所有对 HashSet 的操作其实就是对 HashMap 的操作。所以 HashSet 也不保证集合的顺序,也不是线程安全的容器。
HashMap 的底层结构
JDK1.7 中,HashMap 采用位桶 + 链表的实现,即使用链表来处理冲突,同一 hash 值的链表都存储在一个数组中。但是当位于一个桶中的元素较多,即 hash 值相等的元素较多时,通过 key 值依次查找的效率较低。
所以,与 JDK 1.7 相比,JDK 1.8 在底层结构方面做了一些改变,当每个桶中元素大于 8 的时候,会转变为红黑树,目的就是优化查询效率。
HashMap 的长度为什么是 2 的幂次方
这道题我想了几天,之前和群里小伙伴们探讨每日一题的时候,问他们为什么 length%hash == (n - 1) & hash,它们说相等的前提是 length 的长度 2 的幂次方,然后我回了一句难道 length 还能不是 2 的幂次方吗?其实是我没有搞懂因果关系,因为 HashMap 的长度是 2 的幂次方,所以使用余数来判断在桶中的下标。如果 length 的长度不是 2 的幂次方,小伙伴们可以举个例子来试试
例如长度为 9 时候,3 & (9-1) = 0,2 & (9-1) = 0 ,都在 0 上,碰撞了;
这样会增大 HashMap 碰撞的几率。
HashMap 多线程操作导致死循环问题
HashMap 不是一个线程安全的容器,在高并发场景下,应该使用 ConcurrentHashMap,在多线程场景下使用 HashMap 会造成死循环问题(基于 JDK1.7),出现问题的位置在 rehash 处,也就是
do {Entry<K,V> next = e.next; // <--假设线程一执行到这里就被调度挂起了int i = indexFor(e.hash, newCapacity);e.next = newTable[i];newTable[i] = e;e = next;
} while (e != null);
这是 JDK1.7 的 rehash 代码片段,在并发的场景下会形成环。
JDK1.8 也会造成死循环问题。
HashMap 线程安全的实现有哪些
因为 HashMap 不是一个线程安全的容器,所以并发场景下推荐使用 ConcurrentHashMap ,或者使用线程安全的 HashMap,使用 Collections 包下的线程安全的容器,比如说
Collections.synchronizedMap(new HashMap());
还可以使用 HashTable ,它也是线程安全的容器,基于 key-value 存储,经常用 HashMap 和 HashTable 做比较就是因为 HashTable 的数据结构和 HashMap 相同。
上面效率最高的就是 ConcurrentHashMap。
讲一下 HashMap put 的过程
首先会使用 hash 函数来计算 key,然后执行真正的插入方法
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {Node<K,V>[] tab; Node<K,V> p; int n, i;// 如果table 为null 或者没有为table分配内存,就resize一次if ((tab = table) == null || (n = tab.length) == 0)n = (tab = resize()).length;// 指定hash值节点为空则直接插入,这个(n - 1) & hash才是表中真正的哈希if ((p = tab[i = (n - 1) & hash]) == null)tab[i] = newNode(hash, key, value, null);// 如果不为空else {Node<K,V> e; K k;// 计算表中的这个真正的哈希值与要插入的key.hash相比if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))e = p;// 若不同的话,并且当前节点已经在 TreeNode 上了else if (p instanceof TreeNode)// 采用红黑树存储方式e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);// key.hash 不同并且也不再 TreeNode 上,在链表上找到 p.next==nullelse {for (int binCount = 0; ; ++binCount) {if ((e = p.next) == null) {// 在表尾插入p.next = newNode(hash, key, value, null);// 新增节点后如果节点个数到达阈值,则进入 treeifyBin() 进行再次判断if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1sttreeifyBin(tab, hash);break;}// 如果找到了同hash、key的节点,那么直接退出循环if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))break;// 更新 p 指向下一节点p = e;}}// map中含有旧值,返回旧值if (e != null) { // existing mapping for keyV oldValue = e.value;if (!onlyIfAbsent || oldValue == null)e.value = value;afterNodeAccess(e);return oldValue;}}// map调整次数 + 1++modCount;// 键值对的数量达到阈值,需要扩容if (++size > threshold)resize();afterNodeInsertion(evict);return null;
}
HashMap put 方法的核心就是在 putval 方法,它的插入过程如下
- 首先会判断 HashMap 中是否是新构建的,如果是的话会首先进行 resize
- 然后判断需要插入的元素在 HashMap 中是否已经存在(说明出现了碰撞情况),如果不存在,直接生成新的k-v 节点存放,再判断是否需要扩容。
- 如果要插入的元素已经存在的话,说明发生了冲突,这就会转换成链表或者红黑树来解决冲突,首先判断链表中的 hash,key 是否相等,如果相等的话,就用新值替换旧值,如果节点是属于 TreeNode 类型,会直接在红黑树中进行处理,如果 hash ,key 不相等也不属于 TreeNode 类型,会直接转换为链表处理,进行链表遍历,如果链表的 next 节点是 null,判断是否转换为红黑树,如果不转换的话,在遍历过程中找到 key 完全相等的节点,则用新节点替换老节点
ConcurrentHashMap 底层实现
ConcurrentHashMap 是线程安全的 Map,它也是高并发场景下的首选数据结构,ConcurrentHashMap 底层是使用分段锁来实现的。
Integer 缓存池
Integer 缓存池也就是 IntegerCache ,它是 Integer 的静态内部类。

它的默认值用于缓存 -128 - 127 之间的数字,如果有 -128 - 127 之间的数字的话,使用 new Integer 不用创建对象,会直接从缓存池中取,此操作会减少堆中对象的分配,有利于提高程序的运行效率。
例如创建一个 Integer a = 24,其实是调用 Integer 的 valueOf ,可以通过反编译得出这个结论

然后我们看一下 valueOf 方法

如果在指定缓存池范围内的话,会直接返回缓存的值而不用创建新的 Integer 对象。
缓存的大小可以使用 XX:AutoBoxCacheMax 来指定,在 VM 初始化时,java.lang.Integer.IntegerCache.high 属性会设置和保存在 sun.misc.VM 的私有系统属性中。
UTF-8 和 Unicode 的关系
由于每个国家都有自己独有的字符编码,所以Unicode 的发展旨在创建一个新的标准,用来映射当今使用的大多数语言中的字符,这些字符有一些不是必要的,但是对于创建文本来说却是不可或缺的。Unicode 统一了所有字符的编码,是一个 Character Set,也就是字符集,字符集只是给所有的字符一个唯一编号,但是却没有规定如何存储,不同的字符其存储空间不一样,有的需要一个字节就能存储,有的则需要2、3、4个字节。
UTF-8 只是众多能够对文本字符进行解码的一种方式,它是一种变长的方式。UTF-8 代表 8 位一组表示 Unicode 字符的格式,使用 1 - 4 个字节来表示字符。
U+ 0000 ~ U+ 007F: 0XXXXXXX
U+ 0080 ~ U+ 07FF: 110XXXXX 10XXXXXX
U+ 0800 ~ U+ FFFF: 1110XXXX 10XXXXXX 10XXXXXX
U+10000 ~ U+1FFFF: 11110XXX 10XXXXXX 10XXXXXX 10XXXXXX
可以看到,UTF-8 通过开头的标志位位数实现了变长。对于单字节字符,只占用一个字节,实现了向下兼容 ASCII,并且能和 UTF-32 一样,包含 Unicode 中的所有字符,又能有效减少存储传输过程中占用的空间。
项目为 UTF-8 环境,char c = ‘中’,是否合法
可以,因为 Unicode 编码采用 2 个字节的编码,UTF-8 是 Unicode 的一种实现,它使用可变长度的字符集进行编码,char c = ‘中’ 是两个字节,所以能够存储。合法。
Arrays.asList 获得的 List 应该注意什么
Arrays.asList 是 Array 中的一个静态方法,它能够实现把数组转换成为 List 序列,需要注意下面几点
- Arrays.asList 转换完成后的 List 不能再进行结构化的修改,什么是结构化的修改?就是不能再进行任何 List 元素的增加或者减少的操作。
public static void main(String[] args) {Integer[] integer = new Integer[] { 1, 2, 3, 4 };List integetList = Arrays.asList(integer);integetList.add(5);
}
结果会直接抛出
Exception in thread "main" java.lang.UnsupportedOperationException
我们看一下源码就能发现问题
// 这是 java.util.Arrays 的内部类,而不是 java.util.ArrayList
private static class ArrayList<E> extends AbstractList<E>implements RandomAccess, java.io.Serializable
继承 AbstractList 中对 add、remove、set 方法是直接抛异常的,也就是说如果继承的子类没有去重写这些方法,那么子类的实例去调用这些方法是会直接抛异常的。
下面是AbstractList中方法的定义,我们可以看到具体抛出的异常:
public void add(int index, E element) {throw new UnsupportedOperationException();
}
public E remove(int index) {throw new UnsupportedOperationException();
}
public E set(int index, E element) {throw new UnsupportedOperationException();
}
虽然 set 方法也抛出了一场,但是由于 内部类 ArrayList 重写了 set 方法,所以支持其可以对元素进行修改。

- Arrays.asList 不支持基础类型的转换
Java 中的基础数据类型(byte,short,int,long,float,double,boolean)是不支持使用 Arrays.asList 方法去转换的
Collection 和 Collections 的区别
Collection 和 Collections 都是位于 java.util 包下的类
Collection 是集合类的父类,它是一个顶级接口,大部分抽象类比如说 AbstractList、AbstractSet 都继承了 Collection 类,Collection 类只定义一节标准方法比如说 add、remove、set、equals 等,具体的方法由抽象类或者实现类去实现。
Collections 是集合类的工具类,Collections 提供了一些工具类的基本使用
- sort 方法,对当前集合进行排序, 实现 Comparable 接口的类,只能使用一种排序方案,这种方案叫做自然比较
- 比如实现线程安全的容器
Collections.synchronizedList、Collections.synchronizedMap等 - reverse 反转,使用 reverse 方法可以根据元素的自然顺序 对指定列表按降序进行排序。
- fill,使用指定元素替换指定列表中的所有元素。
有很多用法,读者可以翻阅 Collections 的源码查看,Collections 不能进行实例化,所以 Collections 中的方法都是由 Collections.方法 直接调用。
你知道 fail-fast 和 fail-safe 吗
fail-fast 是 Java 中的一种快速失败机制,java.util 包下所有的集合都是快速失败的,快速失败会抛出 ConcurrentModificationException 异常,fail-fast 你可以把它理解为一种快速检测机制,它只能用来检测错误,不会对错误进行恢复,fail-fast 不一定只在多线程环境下存在,ArrayList 也会抛出这个异常,主要原因是由于 modCount 不等于 expectedModCount。
fail-safe 是 Java 中的一种 安全失败 机制,它表示的是在遍历时不是直接在原集合上进行访问,而是先复制原有集合内容,在拷贝的集合上进行遍历。 由于迭代时是对原集合的拷贝进行遍历,所以在遍历过程中对原集合所作的修改并不能被迭代器检测到,所以不会触发 ConcurrentModificationException。java.util.concurrent 包下的容器都是安全失败的,可以在多线程条件下使用,并发修改。
ArrayList、LinkedList 和 Vector 的区别
这也是一道老生常谈的问题了
ArrayList、LinkedList、Vector 都是位于 java.util 包下的工具类,它们都实现了 List 接口。
- ArrayList 的底层是动态数组,它是基于数组的特性而演变出来的,所以ArrayList 遍历访问非常快,但是增删比较慢,因为会涉及到数组的拷贝。ArrayList 是一个非线程安全的容器,在并发场景下会造成问题,如果想使用线程安全的容器的话,推荐使用
Collections.synchronizedList;ArrayList 在扩容时会增加 50% 的容量。 - LinkedList 的底层是双向链表,所以 LinkedList 的增加和删除非常快,只需把元素删除,把各自的指针指向新的元素即可。但是 LinkedList 遍历比较慢,因为只有每次访问一个元素才能知道下一个元素的值。LinkedList 也是一个非线程安全的容器,推荐使用
Collections.synchronizedList - Vector 向量是最早出现的集合容器,Vector 是一个线程安全的容器,它的每个方法都粗暴的加上了
synchronized锁,所以它的增删、遍历效率都很低。Vector 在扩容时,它的容量会增加一倍。
Exception 和 Error 有什么区别
Exception 泛指的是 异常,Exception 主要分为两种异常,一种是编译期出现的异常,称为 checkedException ,一种是程序运行期间出现的异常,称为 uncheckedException,常见的 checkedException 有 IOException,uncheckedException 统称为 RuntimeException,常见的 RuntimeException 主要有NullPointerException、 IllegalArgumentException、ArrayIndexOutofBoundException等,Exception 可以被捕获。
Error 是指程序运行过程中出现的错误,通常情况下会造成程序的崩溃,Error 通常是不可恢复的,Error 不能被捕获。
详细可以参考这篇文章 看完这篇 Exception 和 Error ,和面试官扯皮就没问题了
String、StringBuilder 和 StringBuffer 有什么区别
String 特指的是 Java 中的字符串,String 类位于 java.lang 包下,String 类是由 final 修饰的,String 字符串一旦创建就不能被修改,任何对 String 进行修改的操作都相当于重新创建了一个字符串。String 字符串的底层使用 StringBuilder 来实现的
StringBuilder 位于 java.util 包下,StringBuilder 是一非线程安全的容器,StringBuilder 的 append 方法常用于字符串拼接,它的拼接效率要比 String 中 + 号的拼接效率高。StringBuilder 一般不用于并发环境
StringBuffer 位于 java.util 包下,StringBuffer 是一个线程安全的容器,多线程场景下一般使用 StringBuffer 用作字符串的拼接
StringBuilder 和 StringBuffer 都是继承于AbstractStringBuilder 类,AbstractStringBuilder 类实现了 StringBuffer 和 StringBuilder 的常规操作。
动态代理是基于什么原理
代理一般分为静态代理和 动态代理,它们都是代理模式的一种应用,静态代理指的是在程序运行前已经编译好,程序知道由谁来执行代理方法。
而动态代理只有在程序运行期间才能确定,相比于静态代理, 动态代理的优势在于可以很方便的对代理类的函数进行统一的处理,而不用修改每个代理类中的方法。可以说动态代理是基于 反射 实现的。通过反射我们可以直接操作类或者对象,比如获取类的定义,获取声明的属性和方法,调用方法,在运行时可以修改类的定义。
动态代理是一种在运行时构建代理、动态处理方法调用的机制。动态代理的实现方式有很多,Java 提供的代理被称为 JDK 动态代理,JDK 动态代理是基于类的继承。
int 和 Integer 的区别
int 和 Integer 区别可就太多了
- int 是 Java 中的基本数据类型,int 代表的是
整型,一个 int 占 4 字节,也就是 32 位,int 的初始值是默认值是 0 ,int 在 Java 内存模型中被分配在栈中,int 没有方法。 - Integer 是 Java 中的基本数据类型的包装类,Integer 是一个对象,Integer 可以进行方法调用,Integer 的默认值是 null,Integer 在 Java 内存模型中被分配在堆中。int 和 Integer 在计算时可以进行相互转换,int -> Integer 的过程称为
装箱,Integer -> int 的过程称为拆箱,Integer 还有 IntegerCache ,会自动缓存 -128 - 127 中的值
Java 提供了哪些 I/O 方式
Java I/O 方式有很多种,传统的 I/O 也称为 BIO,主要流有如下几种
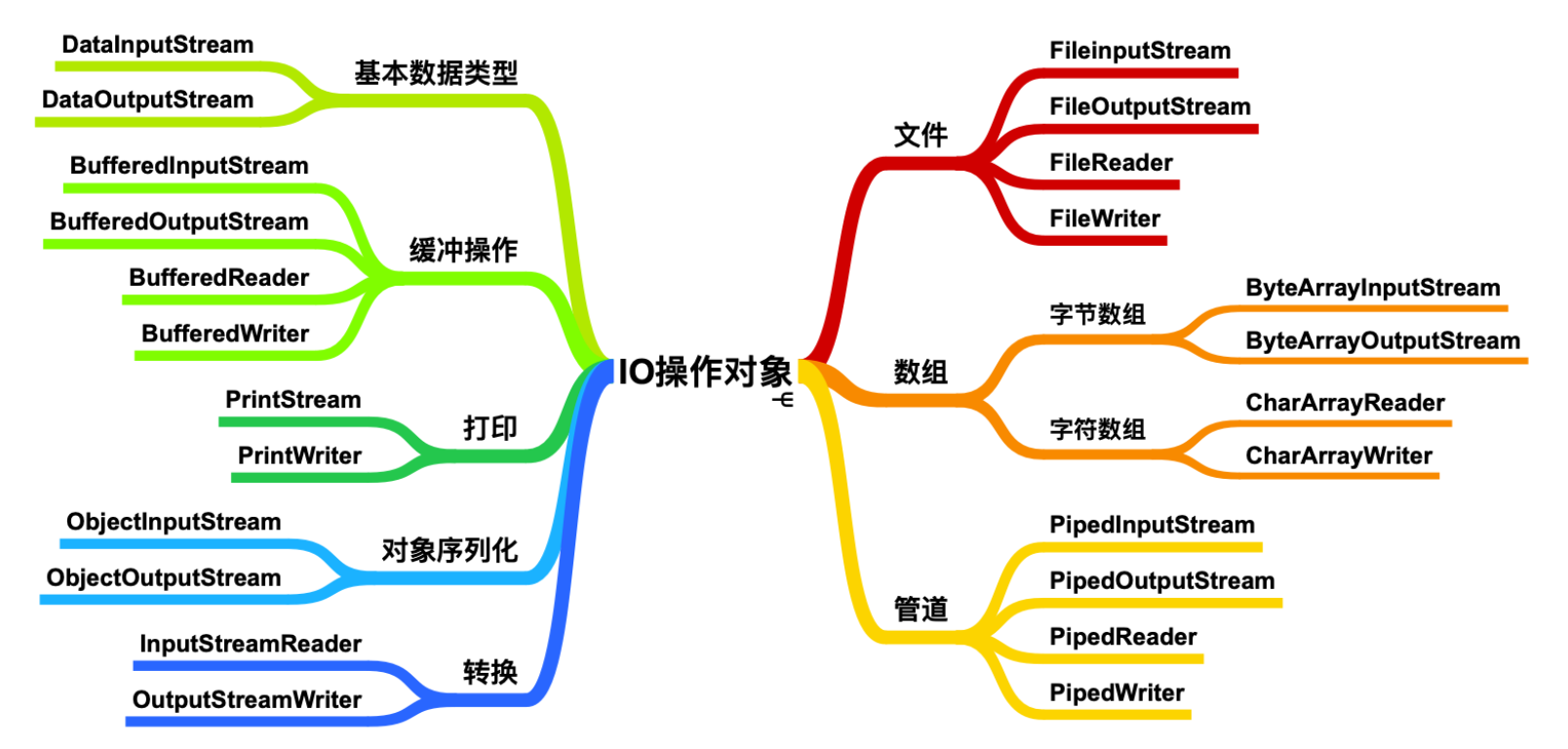
Java I/O 包的实现比较简单,但是容易出现性能瓶颈,传统的 I/O 是基于同步阻塞的。
JDK 1.4 之后提供了 NIO,也就是位于 java.nio 包下,提供了基于 channel、Selector、Buffer的抽象,可以构建多路复用、同步非阻塞 I/O 程序。
JDK 1.7 之后对 NIO 进行了进一步改进,引入了 异步非阻塞 的方式,也被称为 AIO(Asynchronous IO)。可以用生活中的例子来说明:项目经理交给手下员工去改一个 bug,那么项目经理不会一直等待员工解决 bug,他肯定在员工解决 bug 的期间给其他手下分配 bug 或者做其他事情,员工解决完 bug 之后再告诉项目经理 bug 解决完了。
谈谈你知道的设计模式
一张思维导图镇场
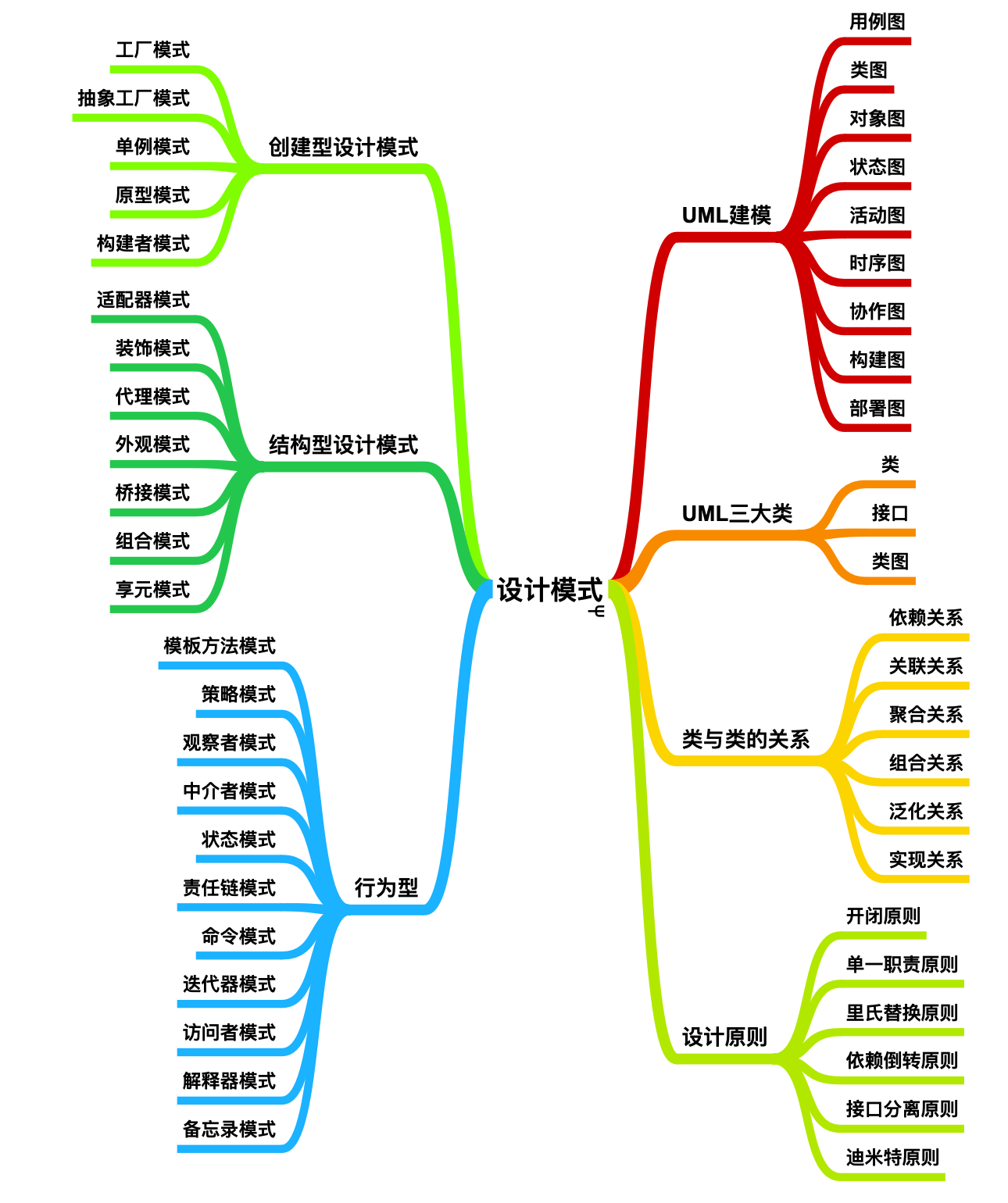
比如全局唯一性可以用 单例模式。
可以使用 策略模式 优化过多的 if…else…
制定标准用 模版模式
接手其他人的锅,但不想改原来的类用 适配器模式
使用 组合 而不是继承
使用 装饰器可以制作加糖、加奶酪的咖啡
代理 可以用于任何中间商…
Comparator 和 Comparable 有什么不同
-
Comparable 更像是自然排序
-
Comparator 更像是定制排序
同时存在时采用 Comparator(定制排序)的规则进行比较。
对于一些普通的数据类型(比如 String, Integer, Double…),它们默认实现了Comparable 接口,实现了 compareTo 方法,我们可以直接使用。
而对于一些自定义类,它们可能在不同情况下需要实现不同的比较策略,我们可以新创建 Comparator 接口,然后使用特定的 Comparator 实现进行比较。
Object 类中一般都有哪些方法
Object 类是所有对象的父类,它里面包含一些所有对象都能够使用的方法
- hashCode():用于计算对象的哈希码
- equals():用于对象之间比较值是否相等
- toString(): 用于把对象转换成为字符串
- clone(): 用于对象之间的拷贝
- wait(): 用于实现对象之间的等待
- notify(): 用于通知对象释放资源
- notifyAll(): 用于通知所有对象释放资源
- finalize(): 用于告知垃圾回收器进行垃圾回收
- getClass(): 用于获得对象类
Java 泛型和类型擦除
关于 Java 泛型和擦除看着一篇就够了。
反射的基本原理,反射创建类实例的三种方式是什么
反射机制就是使 Java 程序在运行时具有自省(introspect) 的能力,通过反射我们可以直接操作类和对象,比如获取某个类的定义,获取类的属性和方法,构造方法等。
创建类实例的三种方式是
- 对象实例.getClass();
- 通过 Class.forName() 创建
- 对象实例.newInstance() 方法创建
强引用、若引用、虚引用和幻象引用的区别
我们说的不同的引用类型其实都是逻辑上的,而对于虚拟机来说,主要体现的是对象的不同的可达性(reachable) 状态和对垃圾收集(garbage collector)的影响。
可以通过下面的流程来对对象的生命周期做一个总结
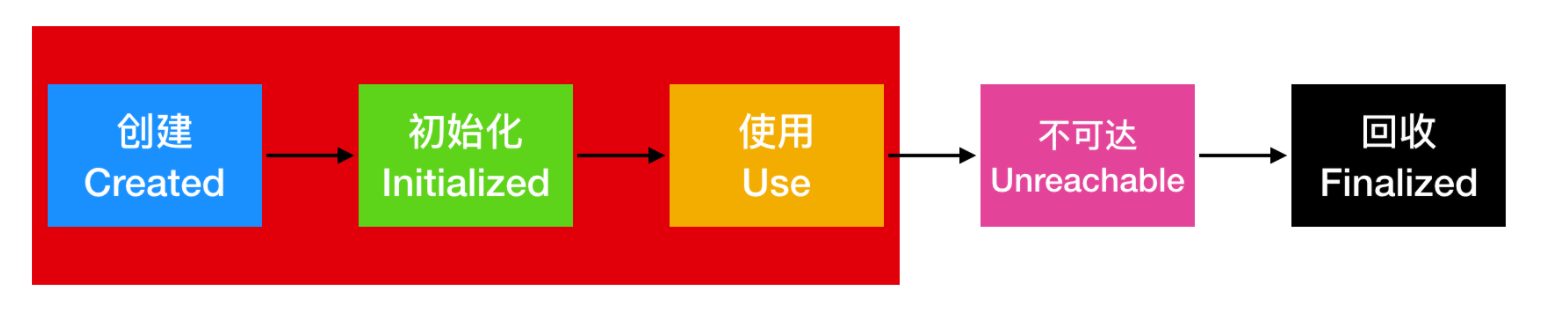
对象被创建并初始化,对象在运行时被使用,然后离开对象的作用域,对象会变成不可达并会被垃圾收集器回收。图中用红色标明的区域表示对象处于强可达阶段。
JDK1.2 介绍了 java.lang.ref 包,对象的生命周期有四个阶段:强可达(Strongly Reachable)、软可达(Soft Reachable)、弱可达(Weak Reachable)、 幻象可达(Phantom Reachable)。

如果只讨论符合垃圾回收条件的对象,那么只有三种:软可达、弱可达和幻象可达。
-
软可达:软可达就是我们只能通过软引用才能访问的状态,软可达的对象是由
SoftReference引用的对象,并且没有强引用的对象。软引用是用来描述一些还有用但是非必须的对象。垃圾收集器会尽可能长时间的保留软引用的对象,但是会在发生OutOfMemoryError之前,回收软引用的对象。如果回收完软引用的对象,内存还是不够分配的话,就会直接抛出 OutOfMemoryError。 -
弱可达:弱可达的对象是
WeakReference引用的对象。垃圾收集器可以随时收集弱引用的对象,不会尝试保留软引用的对象。 -
幻象可达:幻象可达是由
PhantomReference引用的对象,幻象可达就是没有强、软、弱引用进行关联,并且已经被 finalize 过了,只有幻象引用指向这个对象的时候。
除此之外,还有强可达和不可达的两种可达性判断条件
- 强可达:就是一个对象刚被创建、初始化、使用中的对象都是处于强可达的状态
不可达(unreachable):处于不可达的对象就意味着对象可以被清除了。
下面是一个不同可达性状态的转换图

判断可达性条件,也是 JVM 垃圾收集器决定如何处理对象的一部分考虑因素。
所有的对象可达性引用都是 java.lang.ref.Reference 的子类,它里面有一个get() 方法,返回引用对象。 如果已通过程序或垃圾收集器清除了此引用对象,则此方法返回 null 。也就是说,除了幻象引用外,软引用和弱引用都是可以得到对象的。而且这些对象可以人为拯救,变为强引用,例如把 this 关键字赋值给对象,只要重新和引用链上的任意一个对象建立关联即可。
final、finally 和 finalize() 的区别
这三者可以说是没有任何关联之处,我们上面谈到了,final 可以用来修饰类、变量和方法,可以参考上面 final 的那道面试题。
finally 是一个关键字,它经常和 try 块一起使用,用于异常处理。使用 try…finally 的代码块种,finally 部分的代码一定会被执行,所以我们经常在 finally 方法中用于资源的关闭操作。
JDK1.7 中,推荐使用 try-with-resources 优雅的关闭资源,它直接使用 try(){} 进行资源的关闭即可,就不用写 finally 关键字了。
finalize 是 Object 对象中的一个方法,用于对象的回收方法,这个方法我们一般不推荐使用,finalize 是和垃圾回收关联在一起的,在 Java 9 中,将 finalize 标记为了 deprecated, 如果没有特别原因,不要实现 finalize 方法,也不要指望他来进行垃圾回收。
内部类有哪些分类,分别解释一下
在 Java 中,可以将一个类的定义放在另外一个类的定义内部,这就是内部类。内部类本身就是类的一个属性,与其他属性定义方式一致。
内部类的分类一般主要有四种
- 成员内部类
- 局部内部类
- 匿名内部类
- 静态内部类
静态内部类就是定义在类内部的静态类,静态内部类可以访问外部类所有的静态变量,而不可访问外部类的非静态变量;
成员内部类 就是定义在类内部,成员位置上的非静态类,就是成员内部类。成员内部类可以访问外部类所有的变量和方法,包括静态和非静态,私有和公有。
定义在方法中的内部类,就是局部内部类。定义在实例方法中的局部类可以访问外部类的所有变量和方法,定义在静态方法中的局部类只能访问外部类的静态变量和方法。
匿名内部类 就是没有名字的内部类,除了没有名字,匿名内部类还有以下特点:
- 匿名内部类必须继承一个抽象类或者实现一个接口
- 匿名内部类不能定义任何静态成员和静态方法。
- 当所在的方法的形参需要被匿名内部类使用时,必须声明为 final。
- 匿名内部类不能是抽象的,它必须要实现继承的类或者实现的接口的所有抽象方法。
说出几种常用的异常
- NullPointerException: 空指针异常
- NoSuchMethodException:找不到方法
- IllegalArgumentException:不合法的参数异常
- IndexOutOfBoundException: 数组下标越界异常
- IOException:由于文件未找到、未打开或者I/O操作不能进行而引起异常
- ClassNotFoundException :找不到文件所抛出的异常
- NumberFormatException: 字符的UTF代码数据格式有错引起异常;
- InterruptedException: 线程中断抛出的异常
静态绑定和动态绑定的区别
一个Java 程序要经过编写、编译、运行三个步骤,其中编写代码不在我们讨论的范围之内,那么我们的重点自然就放在了编译 和 运行这两个阶段,由于编译和运行阶段过程相当繁琐,下面就我的理解来进行解释:
Java 程序从源文件创建到程序运行要经过两大步骤:
1、编译时期是由编译器将源文件编译成字节码的过程
2、字节码文件由Java虚拟机解释执行
绑定
绑定就是一个方法的调用与调用这个方法的类连接在一起的过程被称为绑定。
绑定主要分为两种:
静态绑定 和 动态绑定
绑定的其他叫法
静态绑定 == 前期绑定 == 编译时绑定
动态绑定 == 后期绑定 == 运行时绑定
为了方便区分: 下面统一称呼为静态绑定和动态绑定
静态绑定
在程序运行前,也就是编译时期 JVM 就能够确定方法由谁调用,这种机制称为静态绑定
识别静态绑定的三个关键字以及各自的理解
如果一个方法由 private、static、final 任意一个关键字所修饰,那么这个方法是前期绑定的
构造方法也是前期绑定
private:private 关键字是私有的意思,如果被 private 修饰的方法是无法由本类之外的其他类所调用的,也就是本类所特有的方法,所以也就由编译器识别此方法是属于哪个类的
public class Person {private String talk;private String canTalk(){return talk;}
}class Animal{public static void main(String[] args) {Person p = new Person();// private 修饰的方法是Person类独有的,所以Animal类无法访问(动物本来就不能说话)
// p.canTalk();}
}
final:final 修饰的方法不能被重写,但是可以由子类进行调用,如果将方法声明为 final 可以有效的关闭动态绑定
public class Fruit {private String fruitName;final String eatingFruit(String name){System.out.println("eating " + name);return fruitName;}
}class Apple extends Fruit{// 不能重写final方法,eatingFruit方法只属于Fruit类,Apple类无法调用
// String eatingFruit(String name){
// super.eatingFruit(name);
// }String eatingApple(String name){return super.eatingFruit(name);}
}
static: static 修饰的方法比较特殊,不用通过 new 出某个类来调用,由类名.变量名直接调用该方法,这个就很关键了,new 很关键,也可以认为是开启多态的导火索,而由类名.变量名直接调用的话,此时的类名是确定的,并不会产生多态,如下代码:
public class SuperClass {public static void sayHello(){System.out.println("由 superClass 说你好");}
}public class SubClass extends SuperClass{public static void sayHello(){System.out.println("由 SubClass 说你好");}public static void main(String[] args) {SuperClass.sayHello();SubClass.sayHello();}
}
SubClass 继承 SuperClass 后,在
是无法重写 sayHello 方法的,也就是说 sayHello() 方法是对子类隐藏的,但是你可以编写自己的 sayHello() 方法,也就是子类 SubClass 的sayHello() 方法,由此可见,方法由 static 关键词所修饰,也是编译时绑定
动态绑定
在运行时根据具体对象的类型进行绑定
除了由 private、final、static 所修饰的方法和构造方法外,JVM 在运行期间决定方法由哪个对象调用的过程称为动态绑定
如果把编译、运行看成一条时间线的话,在运行前必须要进行程序的编译过程,那么在编译期进行的绑定是前期绑定,在程序运行了,发生的绑定就是后期绑定
public class Father {void drinkMilk(){System.out.println("父亲喜欢喝牛奶");}
}public class Son extends Father{@Overridevoid drinkMilk() {System.out.println("儿子喜欢喝牛奶");}public static void main(String[] args) {Father son = new Son();son.drinkMilk();}
}
Son 类继承 Father 类,并重写了父类的 dringMilk() 方法,在输出结果得出的是儿子喜欢喝牛奶。那么上面的绑定方式是什么呢?
上面的绑定方式称之为动态绑定,因为在你编写 Father son = new Son() 的时候,编译器并不知道 son 对象真正引用的是谁,在程序运行时期才知道,这个 son 是一个 Father 类的对象,但是却指向了 Son 的引用,这种概念称之为多态,那么我们就能够整理出来多态的三个原则:
-
继承
-
重写
-
父类引用指向子类对象
也就是说,在 Father son = new Son() ,触发了动态绑定机制。
动态绑定的过程
- 虚拟机提取对象的实际类型的方法表;
- 虚拟机搜索方法签名;
- 调用方法。
动态绑定和静态绑定的特点
静态绑定
静态绑定在编译时期触发,那么它的主要特点是
1、编译期触发,能够提早知道代码错误
2、提高程序运行效率
动态绑定
1、使用动态绑定的前提条件能够提高代码的可用性,使代码更加灵活。
2、多态是设计模式的基础,能够降低耦合性。



















