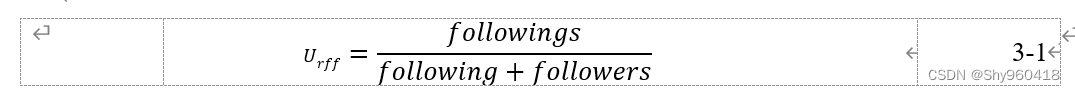11  Logistic模型（计算是/否的概率）

11.1  粗浅理解

我们有m张图片，并且获取了这些图片的特征向量的矩阵，我们需要判断这些图片中是否满足我们某个要求，如是否含有猫🐱这种动物。那么此时我们的每张图片传进模型后的输出就是一个概率。因为概率的大小都是趋于0到1之间的，此时我们就不能利用简单的线性回归来作为输出。我们可以考虑使用logistic回归。logistic回归函数的参数也是一个大小为n的向量，它可以看成是对应每个像素的权重，并且还含有一个b的标量表示偏移。而要实现逻辑回归就需要控制y的输出位于0到1之间，这里利用的方法是使用sigmoid函数，它可以将输出y控制到0-1之间，sigmoid函数如下：

它的函数表达式是： 

 我们可以看到这个函数将输出控制在0-1之间。此时我们的logistic回归的表达式就是：

损失函数和代价函数：
上面我们讨论了logistic回归，我们的目的是要使用这个回归来得到预测输出y，但是我们知道，我们需要一个标准来衡量我们的输出是否好，即训练值中的输出和预测是否一致。而这个衡量标准就是损失函数。对于单个样本，我们定义一个函数loss来计算真实值和预测值的误差：loss=ylog(y^)+(1−y)log(1−y^)
 

当然，你也可以定义一些别的函数作为损失函数，比如就是我们常见的表示数据之间拟合度的函数，不过这些函数会在后面我们拟合时不好拟合，所以我们选择了之前的损失函数。

我们之前使用的loss损失函数只能说是某个样本的拟合情况，而我们需要统计的是对于整个数据集中对应的所有数据的损失函数，我们利用符号J来表示这个函数，这个函数叫做代价函数。J就直接与我们需要训练的W和b相关：

梯度下降法：
之前我们看了代价函数J，我们的目的是需要让它能够变得最少。我们采用的方法就是梯度下降法，即通过求导数的方式将其一步步变化以达到最优解。而我们对于两个变量w和b的处理方式是

上面的两条式子就是用于计算最符合条件（J最小）时的w和b。我们需要变化w和b，使其不断接近最优解，其中式子中的是代表学习率，它的意义是控制w每次变化时变化的步长，而偏导就是控制每次变化的方向。其实就是下图所示从某点开始逐渐往w，b最小的位置移动。

 关于梯度下降我们常用得到求导方法是链式法则

如我们的训练参数只有W1，W2，输入量是X1和X2。我们需要的是J对b、W1和W2进行求导，而这个过程无疑是一个循序渐进的求导过程，因为输出结果到输入结果之间隔着很多中间量，所以我们求导的时候一般都需要使用到链式法则。

我们先从一个样本开始：先算出这个样本的预测值(a)，我们知道：

，根据 我们可以得到损失函数

loss=ylog(y^)+(1−y)log(1−y^)

之后我们可以根据链式法则倒过来求出，而b和W2也类似

在得到损失函数后我们就可以进一步求出