算法：

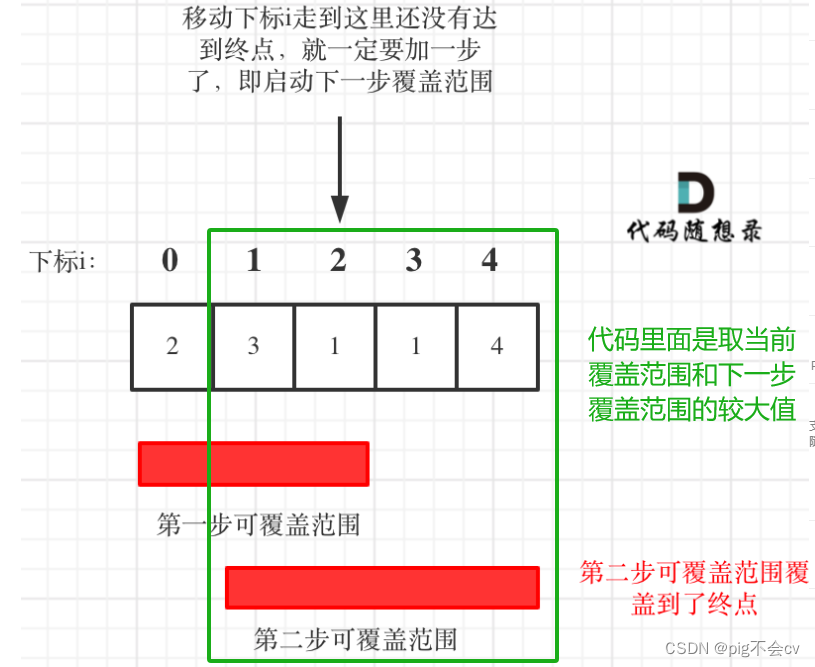
与上一题一样，还是看最大覆盖范围

要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数！

这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

正确代码：

class Solution {public int jump(int[] nums) {if (nums==null || nums.length == 0 || nums.length == 1){return 0;}//记录跳跃的次数int count = 0;//当前的覆盖最大区域int curdistance = 0;//最大的覆盖区域int maxdistance = 0;for (int i=0; i<nums.length;i++){maxdistance = Math.max(maxdistance, i+nums[i]);
//若当前已达终点if (maxdistance>=nums.length-1){count++;break;} 
//若未达终点,且走到当前这步的最大覆盖范围，更新下一步可达的最大区域if (i==curdistance){curdistance = maxdistance;count++;}}return count;}
}

注意：

1.if的条件是 maxdistance>=nums.length-1

是 maxdistance而不是curdistance

索引最大是nums.length-1，一定要减一！

//说明当前一步，再跳一步就到达了末尾if (maxdistance>=nums.length-1){count++;break;} 

`maxdistance` 变量用于记录从当前位置可以到达的最远索引。随着算法在数组中的迭代，该变量会被更新。

当 `maxdistance` 大于或等于 `nums.length - 1` 时，意味着当前位置可以到达数组的末尾或者末尾之后的位置。在这种情况下，算法会增加 `count` 并且跳出循环，因为它已经找到了一条到达末尾的路径。

时间空间复杂度：

• 时间复杂度: O(n)。n是数组长度。
• 空间复杂度: O(1)