文章目录
- 🏳️🌈什么是自动装配
- 🌹SpringBoot的自动装配
- 🍔具体操作

🏳️🌈什么是自动装配
自动装配(Auto-Configuration)是Spring Boot框架的一个核心特性之一,它通过扫描应用程序的classpath和依赖关系,自动配置和装配Spring应用程序所需的各种组件
在传统的Spring应用程序中,开发者需要手动配置大量的bean,例如数据源、事务管理器、视图解析器等。这些配置过程繁琐而容易出错,加大了开发难度和成本。而Spring Boot的自动装配机制则能够自动完成这些配置过程,使得开发者可以更加专注于业务逻辑的实现。
Spring Boot的自动装配实现了以下目标:
- 简化配置:Spring Boot的自动装配能够根据应用程序的需求和条件,自动配置所需的组件,避免了繁琐的手动配置过程。
- 减少出错:由于自动装配是基于条件化配置的,因此可以避免手动配置过程中出现的错误和疏漏。
- 提高效率:自动装配能够提高开发效率,减少开发时间和成本。
- 提升可维护性:自动装配使得应用程序的配置更为规范和标准化,提高了可维护性和可扩展性。
总之,自动装配是Spring Boot的一个重要特性,通过自动配置和装配所需的组件,使得开发者可以更加专注于业务逻辑的实现,提高了开发效率、减少了出错的可能性,并提升了应用程序的可维护性和可扩展性。
🌹SpringBoot的自动装配
当我们使用Spring Boot开发应用程序时,不需要手动配置许多繁琐的细节,而是通过自动装配来简化配置过程。下面将详细解析Spring Boot自动装配的原理和机制:
- 条件注解(Conditional Annotation):Spring Boot使用条件注解来确定是否需要进行自动配置。条件注解基于条件评估,根据一定的条件来判断是否需要进行自动配置。常见的条件注解包括@ConditionalOnClass、@ConditionalOnMissingBean、@ConditionalOnProperty等。
- 自动装配启动过程:在Spring Boot启动过程中,会扫描应用程序的classpath以及依赖关系,根据条件注解的判断结果来决定是否需要进行自动配置。
- Spring Boot Starter依赖:Spring Boot提供了一系列的Starter依赖,每个Starter依赖都定义了一组常用的依赖库,例如spring-boot-starter-web、spring-boot-starter-data-jpa等。这些Starter依赖通过自动配置机制,将所需的组件进行自动装配。
- 自动配置类(Auto-Configuration Class):每个Starter依赖都包含一个或多个自动配置类,这些自动配置类使用条件注解来判断是否需要进行自动配置。自动配置类通常包含@Configuration注解,其中定义了各种bean的创建和配置。
- 自动配置的优先级:在多个自动配置类中,可能存在相同类型的bean的创建和配置。Spring Boot使用自动配置的优先级来决定哪个自动配置类的设置会生效。一般来说,后加载的配置类会覆盖前面的配置类。开发者也可以通过自定义配置来覆盖默认的自动配置。
- 自定义配置:如果应用程序需要对自动配置进行修改或扩展,可以提供自己的配置类。这样可以通过编写自定义的bean来替换或扩展自动配置中的默认行为。
通过自动装配,Spring Boot能够根据应用程序的需求和条件,快速配置并装配所需的组件,使开发者能够专注于业务逻辑而不必过多关注繁琐的配置细节。同时,开发者也可以根据需要进行自定义配置,灵活地调整自动配置的行为。
总结:Spring Boot的自动装配通过条件注解、自动配置类和Starter依赖等机制,根据条件判断和优先级规则来自动配置和装配应用程序所需的组件。这种方式简化了配置过程,提高了开发效率,同时也保留了灵活性,允许开发者进行自定义配置。
🍔具体操作
在SpringBoot的启动类上加上@SpringBootApplication注解,就可以首先自动装配
@SpringBootApplication其实是一个复合注解,真正去首先自动装配的注解是@EnableAutoConfiguration
自动装配的实现主要依靠3个核心的关键技术
-
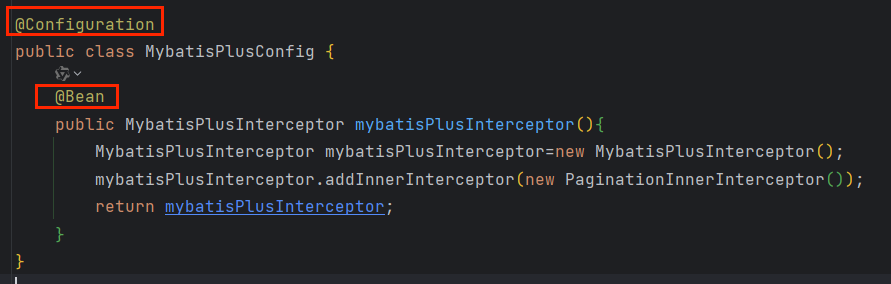
引入starter,启动依赖组件的时候,这个组件里面必须要包含一个@Configuration配置类,而在这个配置类中,我们需要通过@Bean这个注解去声明需要装配到IOC容器里面的Bean对象
-
这个配置类是放在第三方的jar包里面的,然后通过SpringBoot中约定优于配置的这样一个理念,去把这个配置类的全路径放在classpath:/META-INF/spring.factories文件里面,这样子SpringBoot就可以知道第三方jar包里面这个配置类的位置(这个步骤主要用到了Spring里面的SpringFactoriesLoader来完成的)
-
SpringBoot拿到所有第三方jar包里面声明的配置类以后,再通过Spring提供的ImportSelector这一个接口来实现对这些配置类的动态加载,从而完成了自动装配

这样子,让开发人员可以更加聚焦在业务代码的编写上,而不需要去关心和业务无关的配置
在技术的道路上,我们不断探索、不断前行,不断面对挑战、不断突破自我。科技的发展改变着世界,而我们作为技术人员,也在这个过程中书写着自己的篇章。让我们携手并进,共同努力,开创美好的未来!愿我们在科技的征途上不断奋进,创造出更加美好、更加智能的明天!