力扣日记:【回溯算法篇】131. 分割回文串
日期:2023.1.27
参考:代码随想录、力扣
131. 分割回文串
题目描述
难度:中等
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
提示:
- 1 <= s.length <= 16
- s 仅由小写英文字母组成
题解
class Solution {
public:// 关键:将切割问题类比转换为组合问题(树状图)// 但切割与组合最大的不同在于横向遍历时,组合是从集合中取单个值,但切割是截取一个子串 -> for循环时,[startindex, i]表示当前截取的子串(左闭右闭)vector<vector<string>> results; // 组合的集合vector<string> path; // 存储回文子串的组合vector<vector<string>> partition(string s) {backtracking(s, 0);return results;}// 如何判断回文串(双指针,一个从头往后,一个从尾往前,对应相等则为回文串)bool isPalindrome(string s, int startindex, int endindex) {// 左闭右闭while (startindex < endindex) {if (s[startindex] != s[endindex]) {return false;}startindex++;endindex--;}return true;}// 回溯三部曲:// 参数:字符串s以及记录当前截取子串的起始位置startindex(从同一个集合中连续截取,因此需要startindex用于递归纵向遍历)void backtracking(string s, int startindex) {// 终止条件,startindex超过s长度if (startindex == s.size()) { // 左闭,相等即超过// startindex能到最后,说明前面的子串都成功截取为回文串并保存了(否则在for循环将i遍历到最后return)results.push_back(path);return;}// for循环找到回文子串[startindex, i]for (int i = startindex; i < s.size(); i++) {// 是回文子串则截取并递归后面的子串,否则往后遍历找回文子串if (isPalindrome(s, startindex, i)) {// 截取子串并存储path.push_back(s.substr(startindex, i - startindex + 1)); // 注意substr的参数是起始位置以及截取长度backtracking(s, i + 1); // 从i之后的子串递归[i+1, s.size()-1]// 回溯,弹出path.pop_back(); // 之后for向右遍历,尝试截取[startindex, i+1]子串}}}};
复杂度
时间复杂度: O(n * 2^n)
空间复杂度: O(n^2)
思路总结
思路完全参考代码随想录
- 本题实际上算是困难题目
- 难点有以下:
- 将切割问题抽象为组合问题,并转换为树状结构
- 如何模拟那些切割线(如何记录截取子串的始末位置)
- 切割问题中递归如何终止(终止条件)
- 在递归循环中如何截取子串(什么时候该递归,什么时候跳过)
- 如何判断回文
- 将切割问题抽象为组合问题,并转换为树状结构:
-
例如对于字符串abcdef:
组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个…。
切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段…。 - 但切割与组合最大的不同在于横向遍历时,组合是从集合中取单个值[i],但切割是截取一个子串(即[startindex, i])
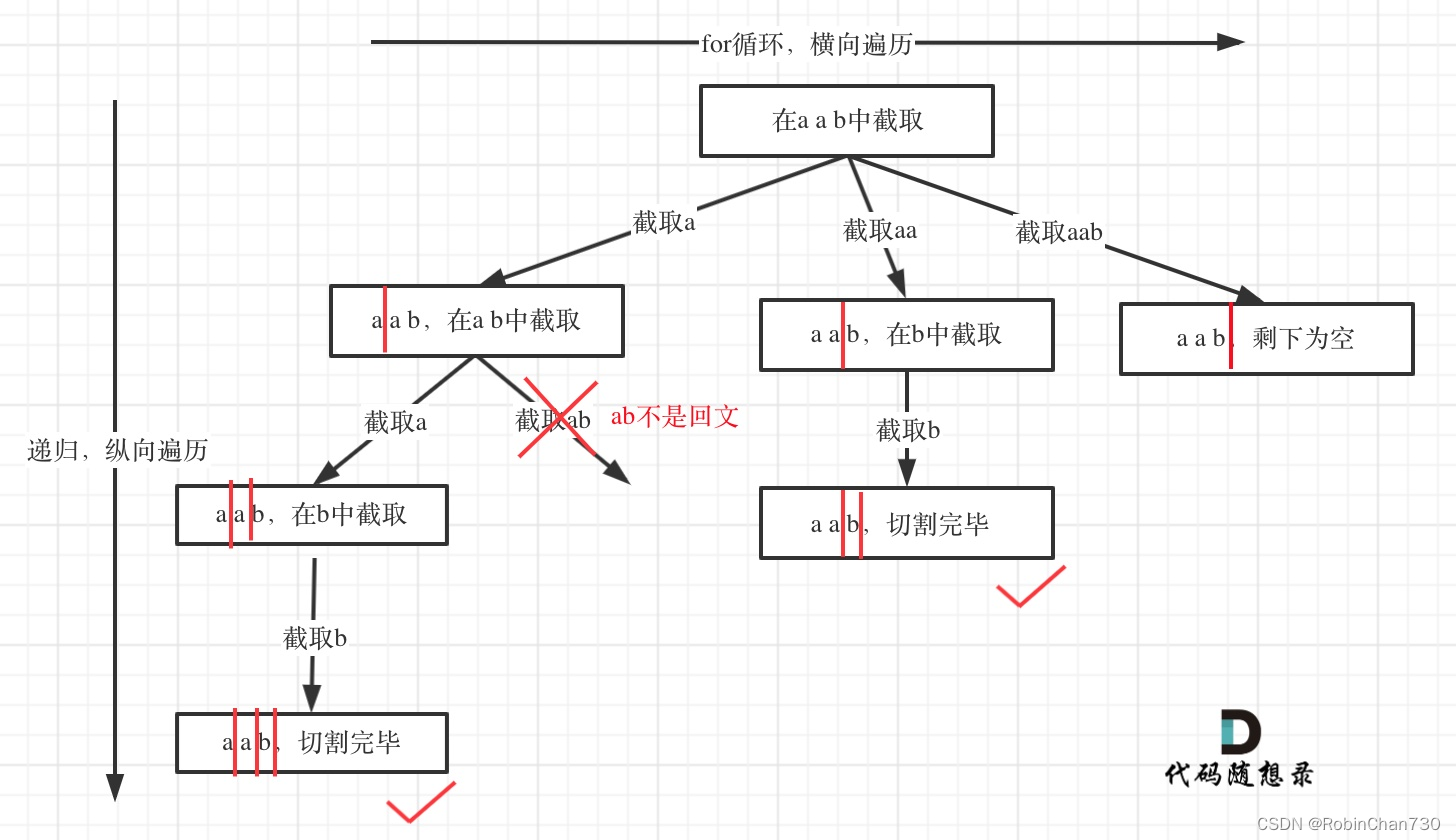
-
- 如何模拟那些切割线(如何记录截取子串的始末位置)
- for循环时,用[startindex, i]表示当前截取的子串(左闭右闭)
- 递归时,startindex = i + 1表示对i之后的子串进行递归截取
- 切割问题中递归如何终止(终止条件)
- startindex超过s长度(由于左闭右闭,相等即超过)
- 因为startindex能到最后,说明前面的子串都成功截取为回文串并保存了(否则在for循环将i遍历到最后return)
- 在递归循环中如何截取子串(什么时候该递归,什么时候跳过)
- 这里是本题“分割回文串”的特征所在,即处理节点(push_back)时要先确保当前for循环要截取的子串是回文串,才能对后面的子串进行递归;否则应该是循环遍历直到当前子串是回文串或结束for循环
- 即递归与回溯,发生的条件是 当前子串是回文子串(类似于40. 组合总和 II中只有满足“当前取的值不重复”的条件才能递归是一样的。所以也可以写成
for(...) {// 不是回文串则跳过if (!isPalindrome(...)) {continue;}// 递归与回溯... }
- 如何判断回文子串:
- 双指针法, 一个从头往后,一个从尾往前,对应相等则为回文串
- TODO:动态规划优化判断回文子串