目录
- 1. 深度恢复
- 1.1 单目相机缺少深度信息
- 1.2 如何恢复场景深度?
- 1.3 深度恢复的思路
- 2. 对极几何约束
- 2.1 直观感受
- 2.2 数学上的描述
1. 深度恢复
1.1 单目相机缺少深度信息
之前学习过相机模型,最经典的就是小孔成像模型。我们知道相机通过小孔成像模型对世界点的观测是缺少深度信息的。我们得到的只是世界点在相机平面上的一个投影。如下图,世界点P只要是在那条红色线上,他在相机上的成像位置就是P‘,所以我们无法知道相机看到的P’对应的世界点的三维位置。
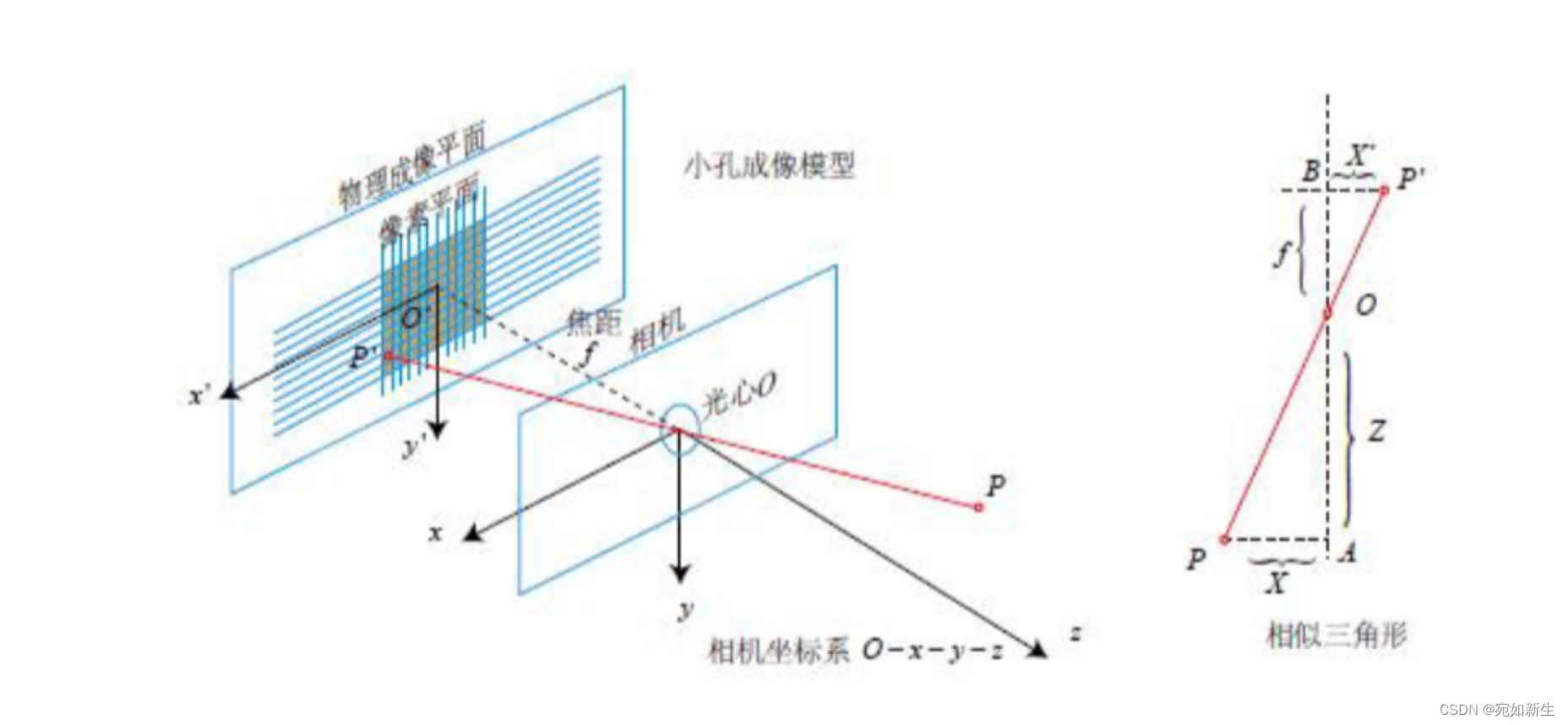
高博的《视觉SLAM十四讲》中一幅画很形象地说明了这个问题。

我们人类看到这个照片,也许会想到,这个明显是“近处的人和远处的人”啊。但是从单目视觉的角度来看,它并不能有“近和远”的概念,因为无论那些远处的人是“真人”还是“模型”,他都会给出这么一副图像,从数据的层面来看,他就是给的二维坐标。
1.2 如何恢复场景深度?
那么,我们很容易想到,我们知道了二维坐标,再知道那些场景的深度不就有立体感了吗?
是的,实际操作起来也很简单,再加一个相机,有两个视角看同一个场景,就能通过三角测距来确定场景点的深度。(就像我们的眼睛一样,我们的双眼就是一个完美的立体视觉系统。有人说我一只眼也能分辨出来远近,那是因为我们长久以来积累下来的“经验”让我们有了一些深度的先验信息。)
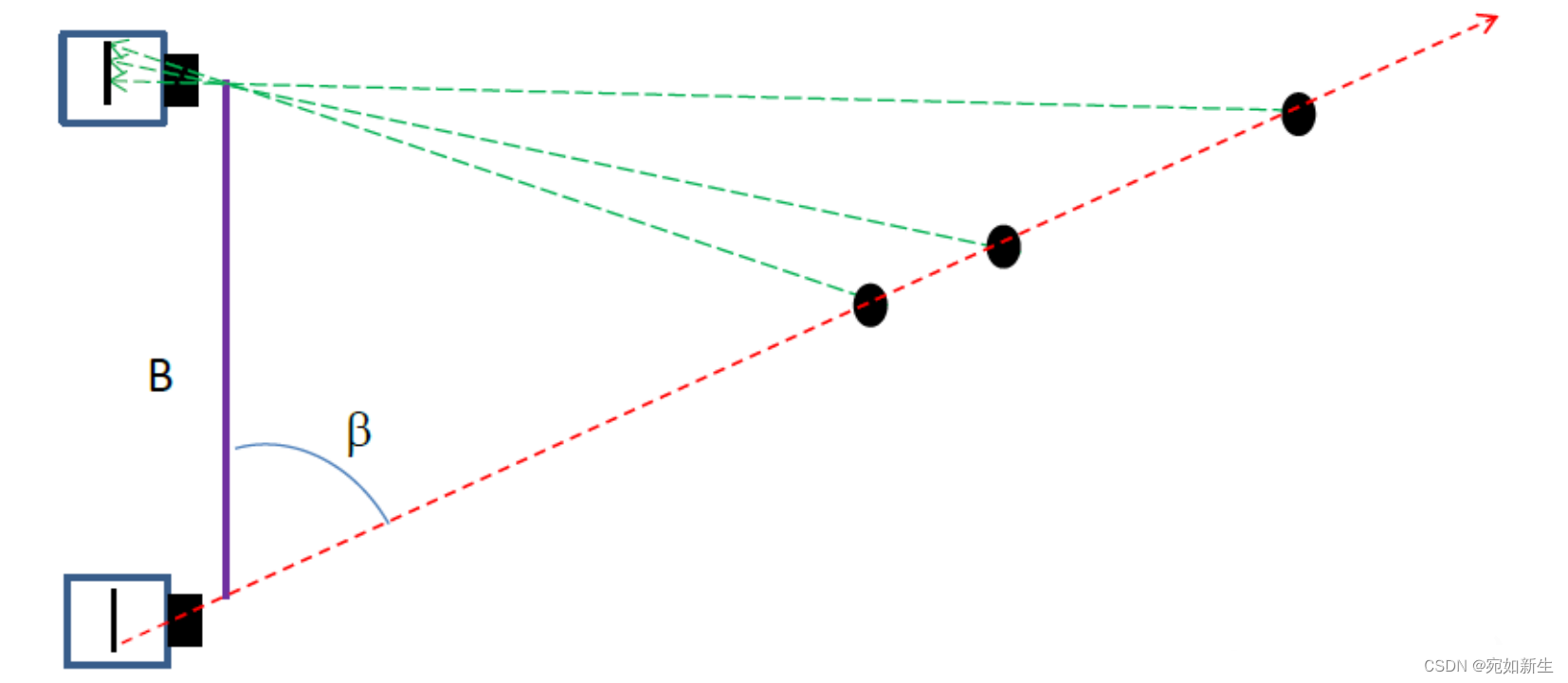
我们来假定一种最理想的情况,两个相机焦距相等,成像平面和光轴完美平行,并且其X轴方向也完美对齐,也就是两个相机不存在Y方向的偏移,那么就会如下图:
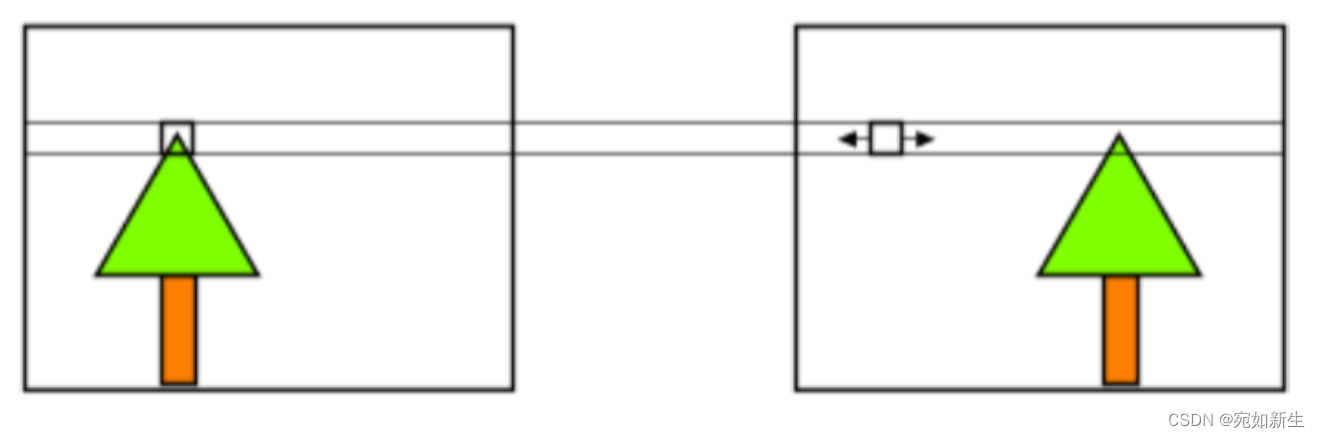
成像示意图可以这么画出来:
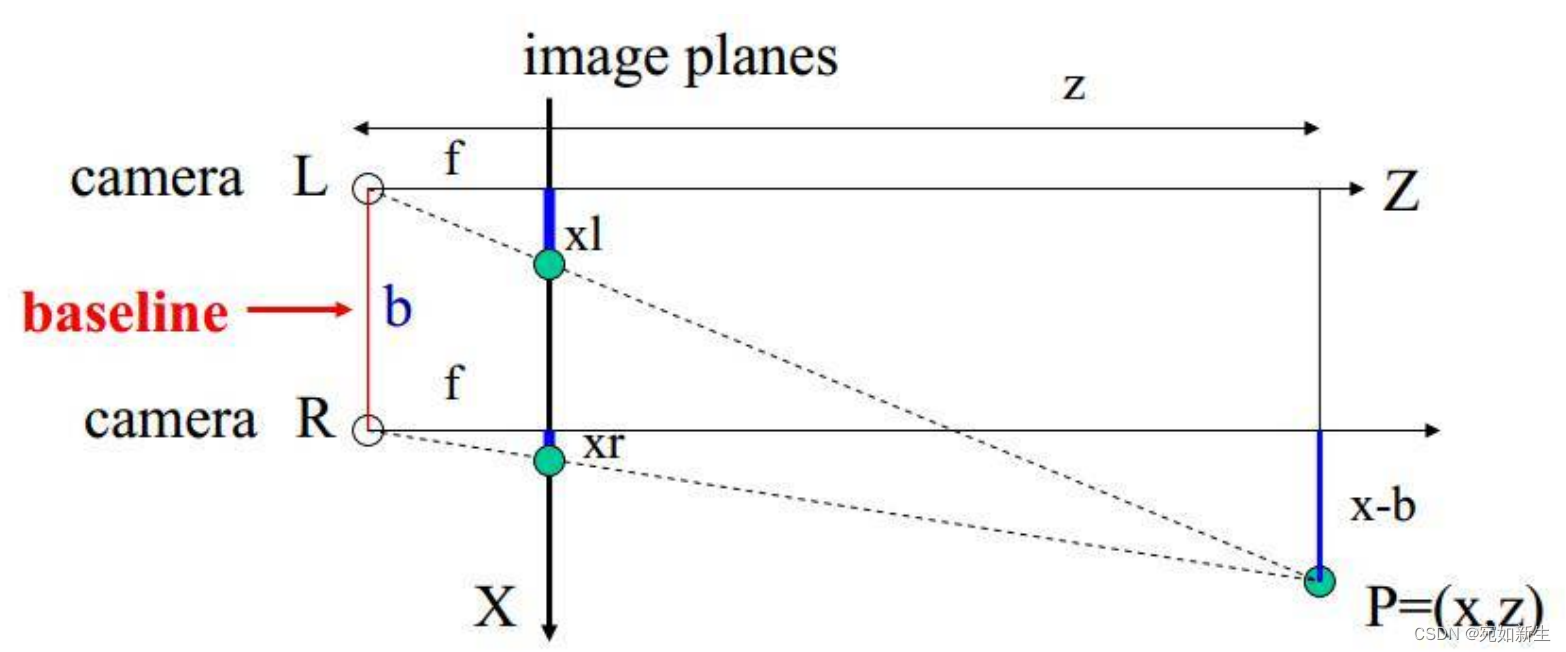
我们从上图可以获得一些信息:左右两个相机,他们三个坐标轴都是平行的,且焦距都是f,两者光心的连线定义为基线。两个相机同时观测到世界点P(当然这里没有考虑y,因为两相机在y方向上没有偏移。有偏移的话一样会形成这样的三角关系。)
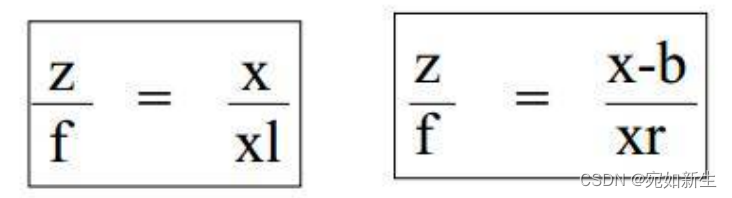
根据相似三角形的性质,会有上述公式成立。很容易得出世界点P的深度值Z:
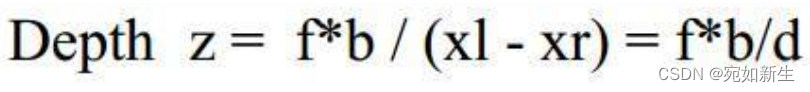
上面的d=(xl - xr)称为视差,从公式上也能看出,场景点符合近大远小的规则。即,f和b不变,深度z与视差d呈反比。
1.3 深度恢复的思路
通过上面的描述,我们就可以总结出深度恢复的答题思路。
①双目相机标定,标定出相机的焦距f和基线b;
②通过某种方式找到两个相机对同一个场景点观测的匹配关系,这一步一般叫做数据关联,得到视差d;
③根据公式计算深度。
2. 对极几何约束
2.1 直观感受
上面的推导我们也说了是一种理想情况,两个相机三个轴完全平行,上面的两个相机x轴还是重合的。但是我们实际使用双目相机的时候基本不可能做到上述情况。实际一般是下图所示情况:
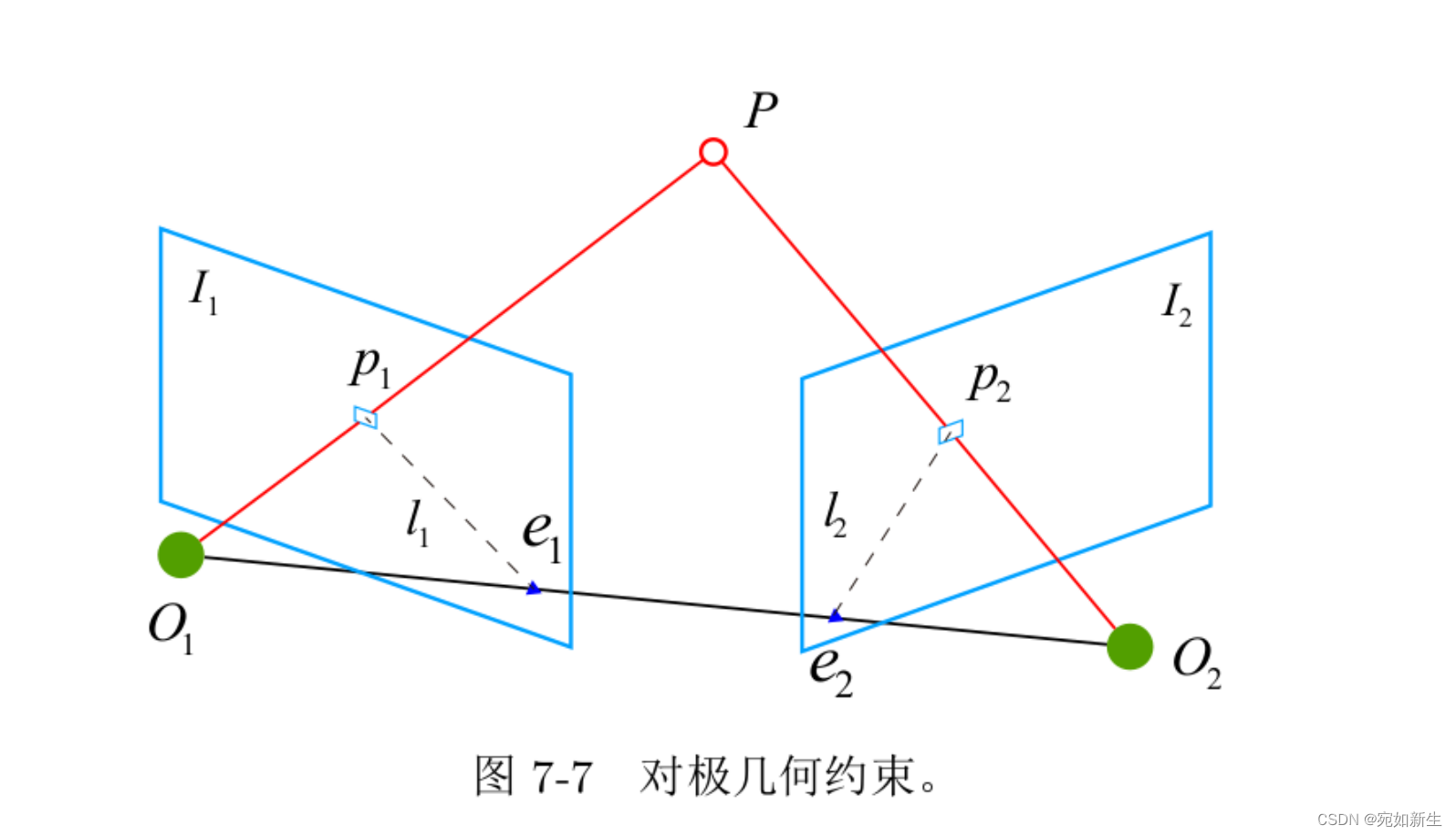
做视觉SLAM的朋友肯定对这个对极几何约束非常熟悉。我在这里只把图上符号含义说明一下: O O O为相机光心位置, I I I为相机的成像平面, P P P是世界点, p p p为两相机各自对世界点的观测, l l l为极线, e e e为极点, O 1 O 2 P O_1O_2P O1O2P组成的平面为极平面,极线为极平面与成像平面的交线。
显然,光心和成像平面是固定的,也就是说极点是固定的,基线也是固定的,而世界点们构成的极平面是绕着基线作为轴转动的,这也造成对极线也是以基线为轴在成像平面内移动。
当然,极点不一定都在画面中,比如第一节中提到的理想情况,极点位置就在无穷远处。这种情况叫做极线矫正,后面会详细说。
对极约束说明了这样一个真相:已知左相机的观测点 p 1 p_1 p1,在右相机的成像平面上寻找匹配点,这个匹配点的位置就在极线上。 有了这个约束,我们不必全图范围内去寻找匹配点,而是沿着极线去寻找即可。双目相机观测到的场景中匹配点的关系如下图,途中白线就是极线。

2.2 数学上的描述
观察对极几何约束的图示,我们重新假设世界点 P P P,在左相机的观测为 P l Pl Pl,在右相机的观测为 P r Pr Pr,则会有如下关系,其中 R R R为两相机的相对旋转, T T T为相对平移。
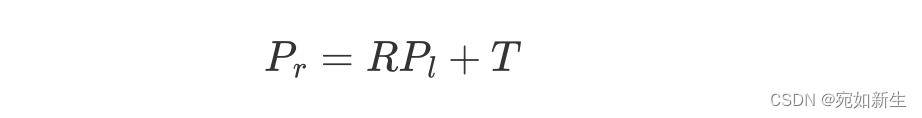
我们在等式两侧同时叉乘一个 T T T,
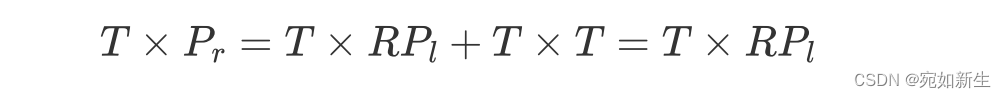
向量和自己叉乘为零,所以有: T T Tx P r = T P_r=T Pr=Tx R P l RP_l RPl。
向量叉乘得到以两向量构成平面的法线,所以上式再与 P r P_r Pr点乘得零。
即, P r T ( T P_r^T(T PrT(Tx R P l ) = 0 RP_l)=0 RPl)=0。
此时,我们定义 E = T E=T E=Tx R R R,则有, P r T E P l = 0 P_r^TEP_l=0 PrTEPl=0。
这就是对极几何约束的数学描述,其中 P l , P r P_l,P_r Pl,Pr为相机成像平面观测的点, E E E为本质矩阵。一般我们会将 P l , P r P_l,P_r Pl,Pr归一化到 z = 1 z=1 z=1的平面上。
当然如果我们使用相机图像像素平面的点来描述对极几何约束,只需在引入一个相机内参,即: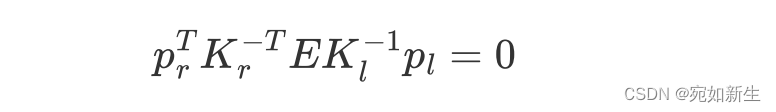
令 F = K r − T E K l − 1 F=K_r^{-T}EK_l^{-1} F=Kr−TEKl−1,这个 F F F被称为基础矩阵。这个时候的 p l , p r p_l,p_r pl,pr就是像素坐标系上的点了。








![[C#]winform部署yolov7+CRNN实现车牌颜色识别车牌号检测识别](https://img-blog.csdnimg.cn/direct/c12aefab36e342e7a127f6e953ac3905.jpeg)


