LinearRegression_GD.py

import numpy as np
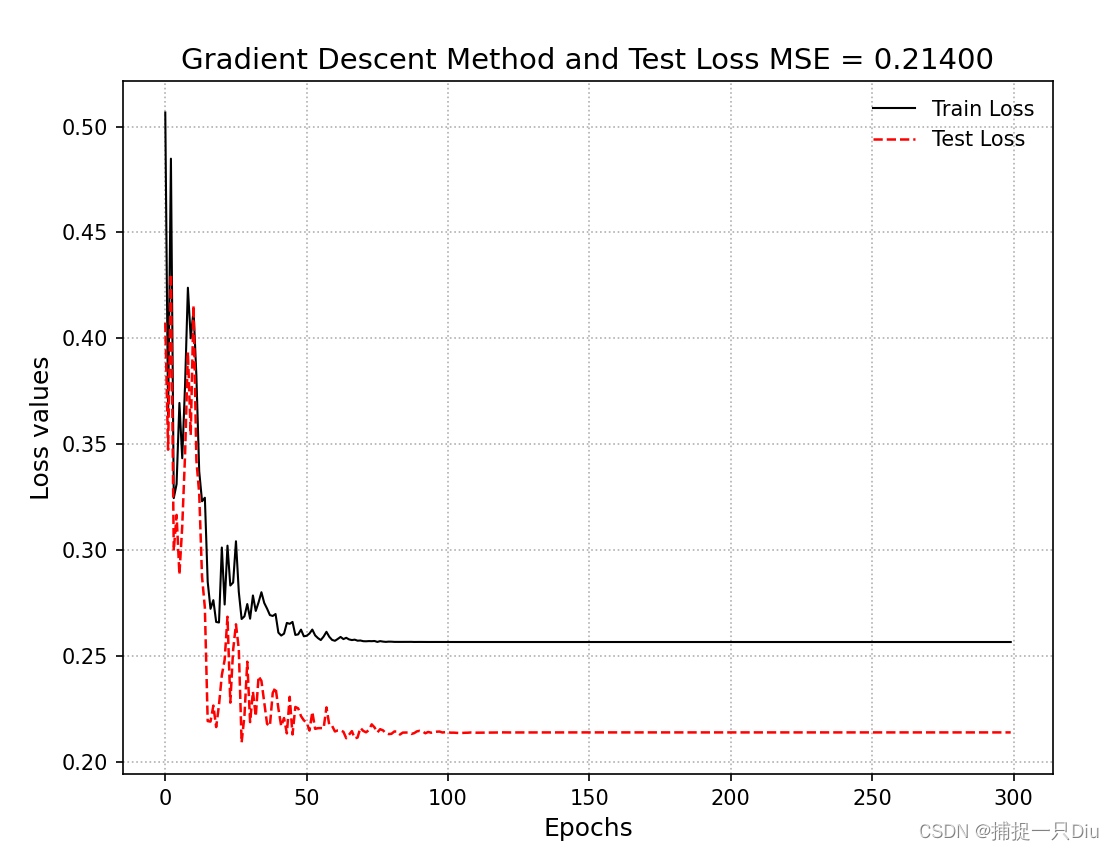
import matplotlib.pyplot as pltclass LinearRegression_GradDesc:"""线性回归，梯度下降法求解模型系数1、数据的预处理：是否训练偏置项fit_intercept（默认True），是否标准化normalized（默认True）2、模型的训练：闭式解公式，fit(self, x_train, y_train)3、模型的预测，predict(self, x_test)4、均方误差，判决系数5、模型预测可视化"""def __init__(self, fit_intercept=True, normalize=True, alpha=0.05, max_epochs=300, batch_size=20):""":param fit_intercept: 是否训练偏置项:param normalize: 是否标准化:param alpha: 学习率:param max_epochs: 最大迭代次数:param batch_size: 批量大小，若为1，则为随机梯度，若为训练集样本量，则为批量梯度，否则为小批量梯度"""self.fit_intercept = fit_intercept  # 线性模型的常数项。也即偏置bias，模型中的theta0self.normalize = normalize  # 是否标准化数据self.alpha = alpha  # 学习率self.max_epochs = max_epochsself.batch_size = batch_sizeself.theta = None  # 训练权重系数if normalize:self.feature_mean, self.feature_std = None, None  # 特征的均值，标准方差self.mse = np.infty  # 训练样本的均方误差self.r2, self.r2_adj = 0.0, 0.0  # 判定系数和修正判定系数self.n_samples, self.n_features = 0, 0  # 样本量和特征数self.train_loss, self.test_loss = [], []  # 存储训练过程中的训练损失和测试损失def init_params(self, n_features):"""初始化参数如果训练偏置项，也包含了bias的初始化:return:"""self.theta = np.random.randn(n_features, 1) * 0.1def fit(self, x_train, y_train, x_test=None, y_test=None):"""模型训练，根据是否标准化与是否拟合偏置项分类讨论:param x_train: 训练样本集:param y_train: 训练目标集:param x_test: 测试样本集:param y_test: 测试目标集:return:"""if self.normalize:self.feature_mean = np.mean(x_train, axis=0)  # 样本均值self.feature_std = np.std(x_train, axis=0) + 1e-8  # 样本方差x_train = (x_train - self.feature_mean) / self.feature_std  # 标准化if x_test is not None:x_test = (x_test - self.feature_mean) / self.feature_std  # 标准化if self.fit_intercept:x_train = np.c_[x_train, np.ones_like(y_train)]  # 添加一列1，即偏置项样本if x_test is not None and y_test is not None:x_test = np.c_[x_test, np.ones_like(y_test)]  # 添加一列1，即偏置项样本self.init_params(x_train.shape[1])  # 初始化参数self._fit_gradient_desc(x_train, y_train, x_test, y_test)  # 梯度下降法训练模型def _fit_gradient_desc(self, x_train, y_train, x_test=None, y_test=None):"""三种梯度下降求解：（1）如果batch_size为1，则为随机梯度下降法（2）如果batch_size为样本量，则为批量梯度下降法（3）如果batch_size小于样本量，则为小批量梯度下降法:return:"""train_sample = np.c_[x_train, y_train]  # 组合训练集和目标集，以便随机打乱样本# np.c_水平方向连接数组，np.r_竖直方向连接数组# 按batch_size更新theta，三种梯度下降法取决于batch_size的大小best_theta, best_mse = None, np.infty  # 最佳训练权重与验证均方误差for i in range(self.max_epochs):self.alpha *= 0.95np.random.shuffle(train_sample)  # 打乱样本顺序，模拟随机化batch_nums = train_sample.shape[0] // self.batch_size  # 批次for idx in range(batch_nums):# 取小批量样本，可以是随机梯度（1），批量梯度（n）或者是小批量梯度（<n）batch_xy = train_sample[self.batch_size * idx: self.batch_size * (idx + 1)]# 分取训练样本和目标样本，并保持维度batch_x, batch_y = batch_xy[:, :-1], batch_xy[:, -1:]# 计算权重更新增量delta = batch_x.T.dot(batch_x.dot(self.theta) - batch_y) / self.batch_sizeself.theta = self.theta - self.alpha * deltatrain_mse = ((x_train.dot(self.theta) - y_train.reshape(-1, 1)) ** 2).mean()self.train_loss.append(train_mse)if x_test is not None and y_test is not None:test_mse = ((x_test.dot(self.theta) - y_test.reshape(-1, 1)) ** 2).mean()self.test_loss.append(test_mse)def get_params(self):"""返回线性模型训练的系数:return:"""if self.fit_intercept:  # 存在偏置项weight, bias = self.theta[:-1], self.theta[-1]else:weight, bias = self.theta, np.array([0])if self.normalize:  # 标准化后的系数weight = weight / self.feature_std.reshape(-1, 1)  # 还原模型系数bias = bias - weight.T.dot(self.feature_mean)return weight.reshape(-1), biasdef predict(self, x_test):"""测试数据预测:param x_test: 待预测样本集，不包括偏置项:return:"""try:self.n_samples, self.n_features = x_test.shape[0], x_test.shape[1]except IndexError:self.n_samples, self.n_features = x_test.shape[0], 1  # 测试样本数和特征数if self.normalize:x_test = (x_test - self.feature_mean) / self.feature_std  # 测试数据标准化if self.fit_intercept:# 存在偏置项，加一列1x_test = np.c_[x_test, np.ones(shape=x_test.shape[0])]y_pred = x_test.dot(self.theta).reshape(-1, 1)return y_preddef cal_mse_r2(self, y_test, y_pred):"""计算均方误差，计算拟合优度的判定系数R方和修正判定系数:param y_pred: 模型预测目标真值:param y_test: 测试目标真值:return:"""self.mse = ((y_test.reshape(-1, 1) - y_pred.reshape(-1, 1)) ** 2).mean()  # 均方误差# 计算测试样本的判定系数和修正判定系数self.r2 = 1 - ((y_test.reshape(-1, 1) - y_pred.reshape(-1, 1)) ** 2).sum() / \((y_test.reshape(-1, 1) - y_test.mean()) ** 2).sum()self.r2_adj = 1 - (1 - self.r2) * (self.n_samples - 1) / \(self.n_samples - self.n_features - 1)return self.mse, self.r2, self.r2_adjdef plt_predict(self, y_test, y_pred, is_show=True, is_sort=True):"""绘制预测值与真实值对比图:return:"""if self.mse is np.infty:self.cal_mse_r2(y_pred, y_test)if is_show:plt.figure(figsize=(8, 6))if is_sort:idx = np.argsort(y_test)  # 升序排列，获得排序后的索引plt.plot(y_test[idx], "k--", lw=1.5, label="Test True Val")plt.plot(y_pred[idx], "r:", lw=1.8, label="Predictive Val")else:plt.plot(y_test, "ko-", lw=1.5, label="Test True Val")plt.plot(y_pred, "r*-", lw=1.8, label="Predictive Val")plt.xlabel("Test sample observation serial number", fontdict={"fontsize": 12})plt.ylabel("Predicted sample value", fontdict={"fontsize": 12})plt.title("The predictive values of test samples \n MSE = %.5e, R2 = %.5f, R2_adj = %.5f"% (self.mse, self.r2, self.r2_adj), fontdict={"fontsize": 14})plt.legend(frameon=False)plt.grid(ls=":")if is_show:plt.show()def plt_loss_curve(self, is_show=True):"""可视化均方损失下降曲线:param is_show: 是否可视化:return:"""if is_show:plt.figure(figsize=(8, 6))plt.plot(self.train_loss, "k-", lw=1, label="Train Loss")if self.test_loss:plt.plot(self.test_loss, "r--", lw=1.2, label="Test Loss")plt.xlabel("Epochs", fontdict={"fontsize": 12})plt.ylabel("Loss values", fontdict={"fontsize": 12})plt.title("Gradient Descent Method and Test Loss MSE = %.5f"% (self.test_loss[-1]), fontdict={"fontsize": 14})plt.legend(frameon=False)plt.grid(ls=":")# plt.axis([0, 300, 20, 30])if is_show:plt.show()

test_linear_regression_gd.py

import numpy as np
from LinearRegression_GD import LinearRegression_GradDesc
from sklearn.model_selection import train_test_splitnp.random.seed(42)
X = np.random.rand(1000, 6)  # 随机样本值，6个特征
coeff = np.array([4.2, -2.5, 7.8, 3.7, -2.9, 1.87])  # 模型参数
y = coeff.dot(X.T) + 0.5 * np.random.randn(1000)  # 目标函数值X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, shuffle=True)lr_gd = LinearRegression_GradDesc(alpha=0.1, batch_size=1)
lr_gd.fit(X_train, y_train, X_test, y_test)
theta = lr_gd.get_params()
print(theta)
y_test_pred = lr_gd.predict(X_test)
lr_gd.plt_predict(y_test, y_test_pred)
lr_gd.plt_loss_curve()