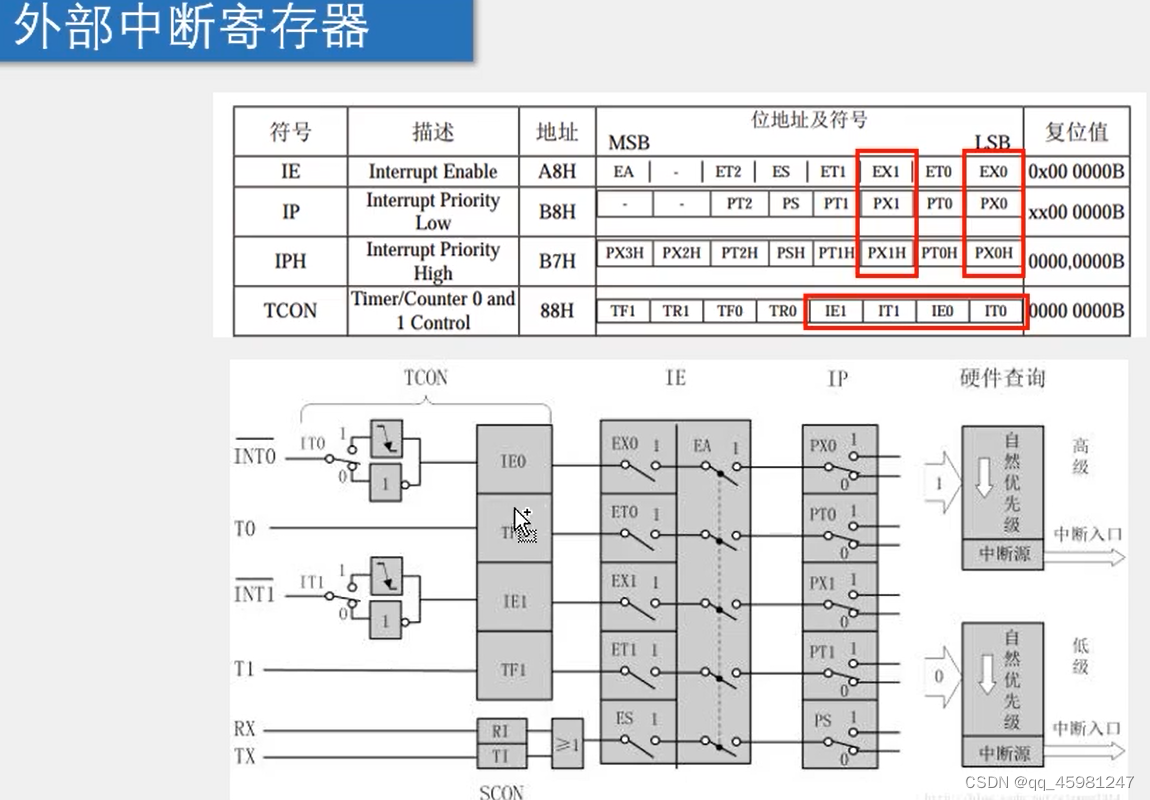
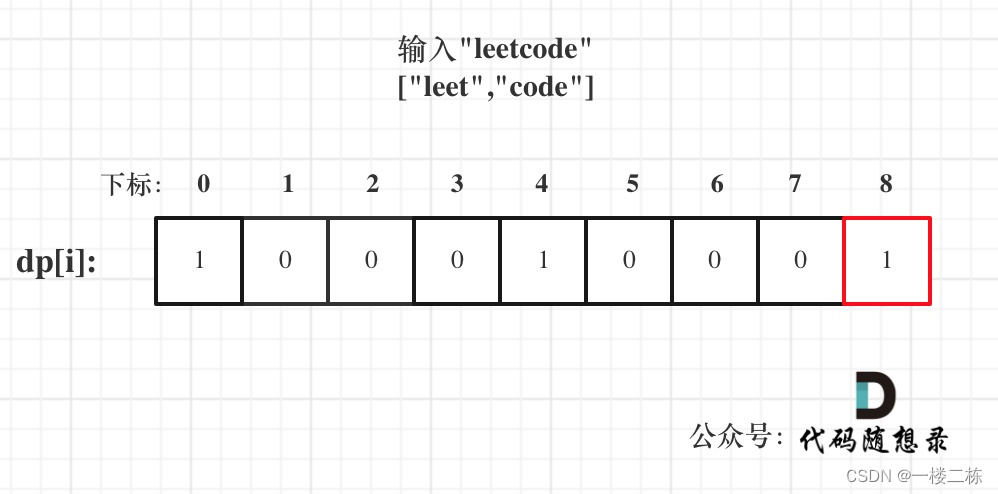
题目:139.单词拆分
文章链接:代码随想录
视频链接:LeetCode:139.单词拆分
题目链接:力扣题目链接
图释:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {// 将字符串的列表装到set数组中,方便查找findunordered_set<string> wordSet(wordDict.begin(), wordDict.end());// dp数组表示,装满i个字符串,能否用字符列表装满vector<bool> dp(s.size()+1, false);dp[0] = true;// 由于字符串需要按排列循序进行,所以是排列问题: 先遍历背包再遍历物品for(int i=1; i<=s.size(); i++){ // 遍历背包 dp[6] = 'leetco'// for(int j=0; j<i; j++){ //遍历物品 从j=0开始增加到j=5 // 截取字符串 j=4 截取 [4, (6-2)] costring word = s.substr(j, i-j); // substr(起始位置,截取个数)// 查找 "co"是否在wordSet中, 以及dp[4]='leet'是都为 trueif(wordSet.find(word) != wordSet.end() && dp[j]){dp[i] = true;}}}return dp[s.size()];}
};题目:多重背包
文章链接:代码随想录
题目链接:卡码网题目链接
图释:将多重背包展开成01背包,每个物品只能用一次


#include<iostream>
#include<vector>
using namespace std;
int main() {int bagWeight,n;cin >> bagWeight >> n;vector<int> weight(n, 0);vector<int> value(n, 0);vector<int> nums(n, 0);for (int i = 0; i < n; i++) cin >> weight[i];for (int i = 0; i < n; i++) cin >> value[i];for (int i = 0; i < n; i++) cin >> nums[i];vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < n; i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包,然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数// k小于物品的数目, k个物品数的重量小于背包的容量dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}cout << dp[bagWeight] << endl;
}
题目:背包问题总结
文章链接:代码随想录
图释:

1、问能否能装满背包(或者最多装多少):
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);2、问装满背包有几种方法:
dp[j] += dp[j - nums[i]];3、问背包装满最大价值:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); 4、问装满背包所有物品的最小个数:
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);遍历顺序:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。如果求排列数就是外层for遍历背包,内层for循环遍历物品。