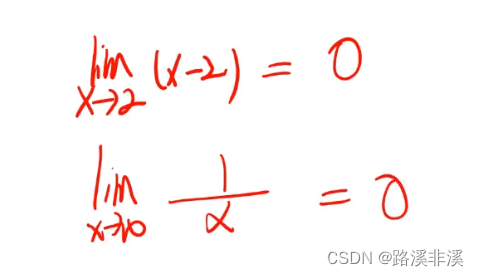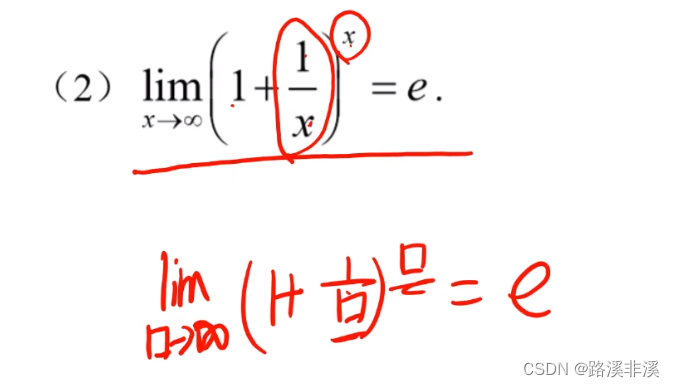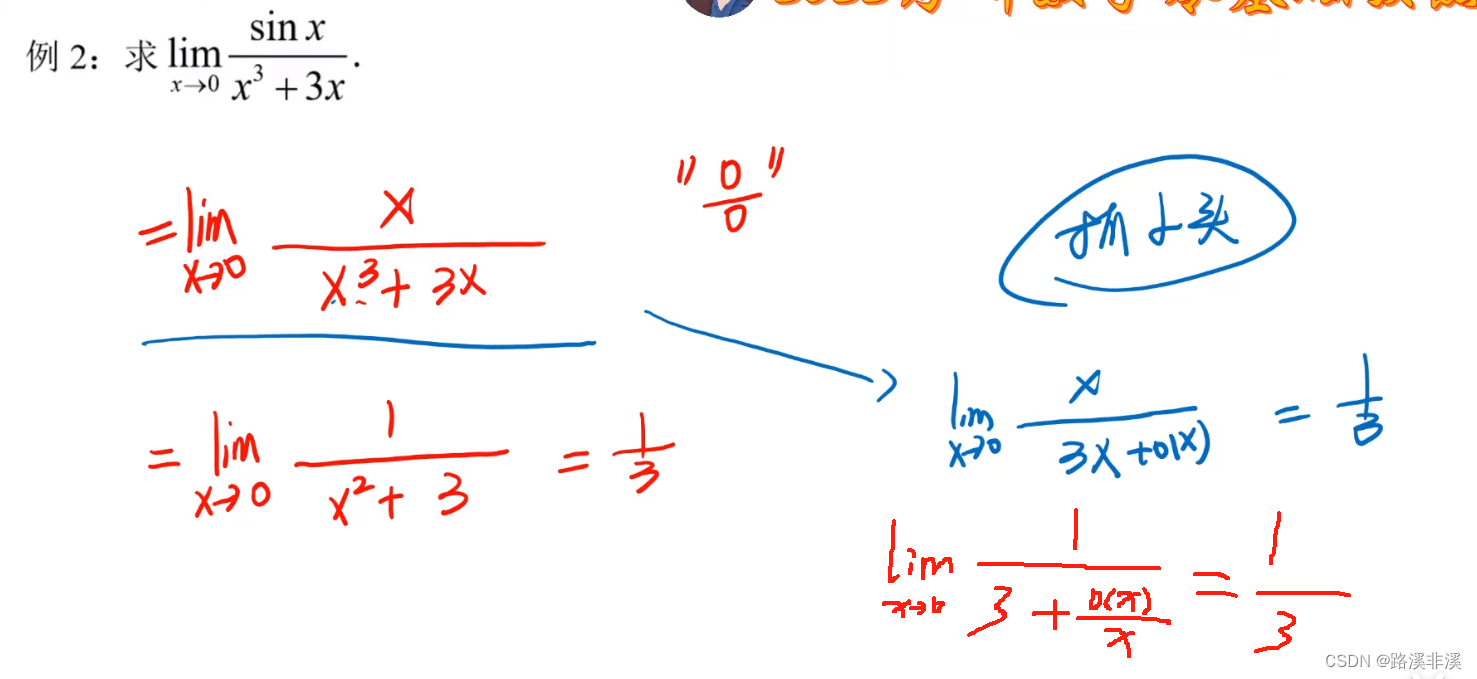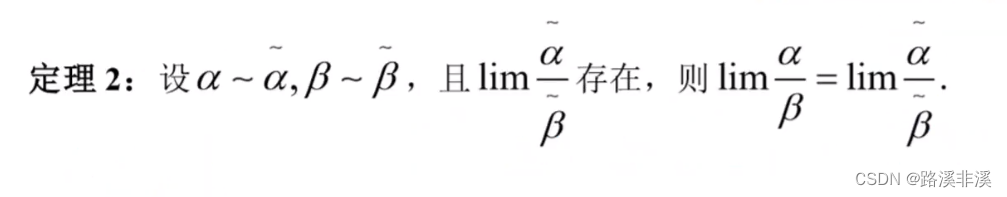参考课程：【建议收藏】同济七版《高等数学》精讲视频 | 期末考试 | 考研零基础 | 高数小白_哔哩哔哩_bilibili

仅供本人学习之用

无穷小

无穷小不是指趋近于负无穷，而是趋近于0

比如

这里x-2就叫做x趋近于2时的无穷小；1/x就叫做x趋近于无穷时的无穷小；

有个误解需要纠正：

0不是无穷小，0是一个实常数，而无穷小是指无限趋近于0的一个变量，两者的概念完全不同。无穷小是一个永远都在变的概念，永远停不下来，永远在向0更进一步，但永远也接触不到，就像一个超级大舔狗。

无穷小是极限为0的变量而不是数量0，是指自变量在一定变动方式下其极限为数量0，称一个函数是无穷小，一定要说明自变量的变化趋势。

无穷大

说的这么绕，其实意思就是当x趋近于x0或者x趋近于无穷时，极限值趋近于无穷，那么称函数f(x)为对应时候的无穷大，函数值正无穷和负无穷都属于无穷大；

这里我一开始有个误解，以为无穷大是函数值的极限为无穷大；

其实，不能这么说，为什么呢？

函数值大于一个很大的数，也就是说函数值趋近于无穷，我们不能说该函数的极限是无穷大，因为当函数值趋近于无穷时，说明极限是不存在的，极限的定义中是函数值趋近于某个常数A。

而无穷小时，就是函数的极限为0，是存在极限的，所以我们关注无穷小比关注无穷大要更多。

注意，定义里只是说函数值的绝对值大于一个很大的数，并没有说它的极限是无穷大，还是很严谨的。

几何意义

无穷小和无穷大的性质

无穷小与函数极限的关系

无穷大和无穷小的关系

这两个性质并不难理解。

极限运算法则

这两个是关于无穷小的相加以及有限个无穷小的乘积仍是无穷小的法则；

 

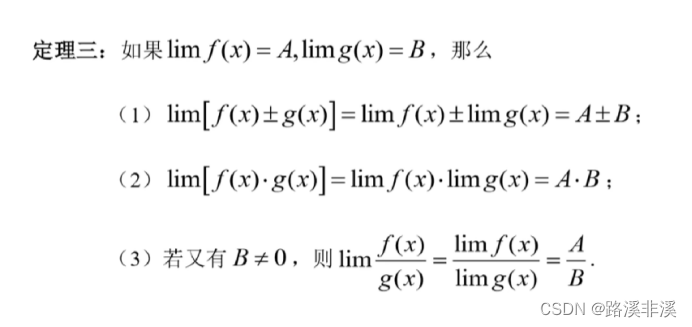
两个函数加减的极限，等于各自极限的加减；

两个函数相乘的极限，等于各自极限的相乘；

两个函数相除的极限，等于各自极限的相除；

定理四是关于数列极限的加减乘除；

可以和定理三放在一起理解记忆；

 

定义五是说，如果一个函数的函数值总是大于等于另一个函数的函数值，那么该函数对应的极限也必然大于等于另一个函数的极限；

 

定理六是关于复合函数的极限法则；

其实就是将复合函数的内层函数看作一个整体，然后当作外层函数的自变量。

看两道题就明白了

这里可以参考课程的1.5节极限的运算法则做几道题，自然就能理解更多了。

极限存在法则

1

夹逼准则

数列的夹逼准则

函数的夹逼准则

2

单调有界准则

这个好像是针对数列的。

两个重要极限

这里如果x是个复合函数，可以当做整体来看待，比如：

无穷小的比较

如果在某个条件（x->x0或者x->∞）下，两个函数都是无穷小，此时可以比较两个无穷小哪个更趋近于无穷小，即哪个趋近于无穷小的程度更高。

比如，当x->0时，x^2和x都是无穷小，但此时，x^2趋向于无穷小的程度更高。

两个无穷小比较，我们可以根据比较结果的极限值来界定趋向的程度。

这里用x^n来举例说明就很好理解。

比如x^5比上x^2，当x->0时，x^5就是比x^2更高阶的无穷小；

x^5和x^5就是等价无穷小，也是同阶无穷小，可以看到，等价无穷小是同阶无穷小的一种特例；

其他可以进行类似的举例来理解。

重点关注高阶无穷小和等价无穷小，等价无穷小在计算极限时可以等价替换。

在求极限时，高阶无穷小的一个变换是这样的，试着理解下：

x^3+x在x->0求极限时可以替换成o(x) + x

比如：

一个x和x的高阶无穷小相加，并且求极限时，x的高阶无穷小可以看做0

重要的等价无穷小

这些等价无穷小是要记住的。

学了这个再回头来看这个重要的极限

因为x->0时，sinx和x是等价无穷小，因此二者比值的极限就等于1

几个重要定理

定理2中的弯弯只是一个符号，可以用任意符号来表示对应的等价无穷小；

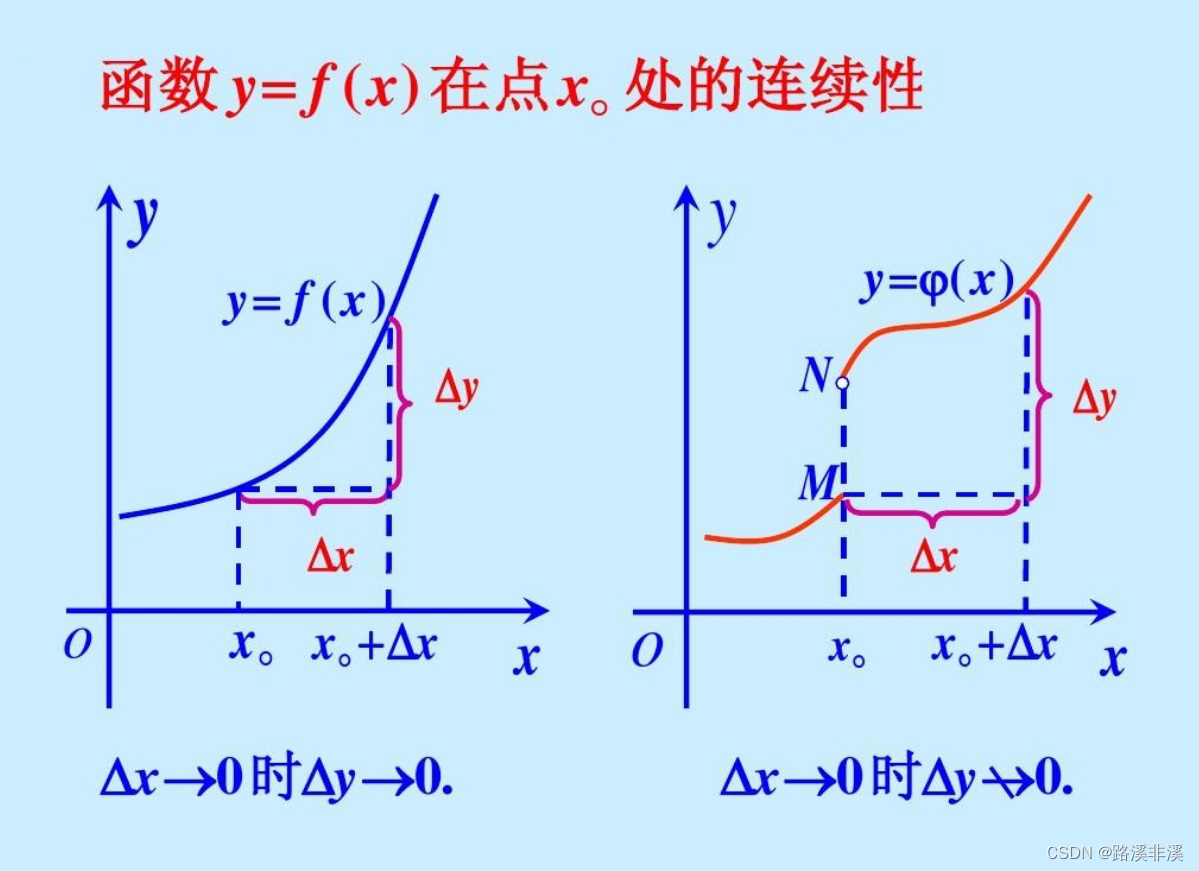
函数的连续性

什么样的函数是连续的？我们对连续的定义是什么呢？

△x趋近于0和x趋近于x0是一样的含义。

下面这张示意图可以帮助理解：

连续函数的性质

间断点

满足三个条件之一即可；

从上到下为：

没有定义；

有定义但是极限不存在；

有定义极限存在但是不满足连续的定义；

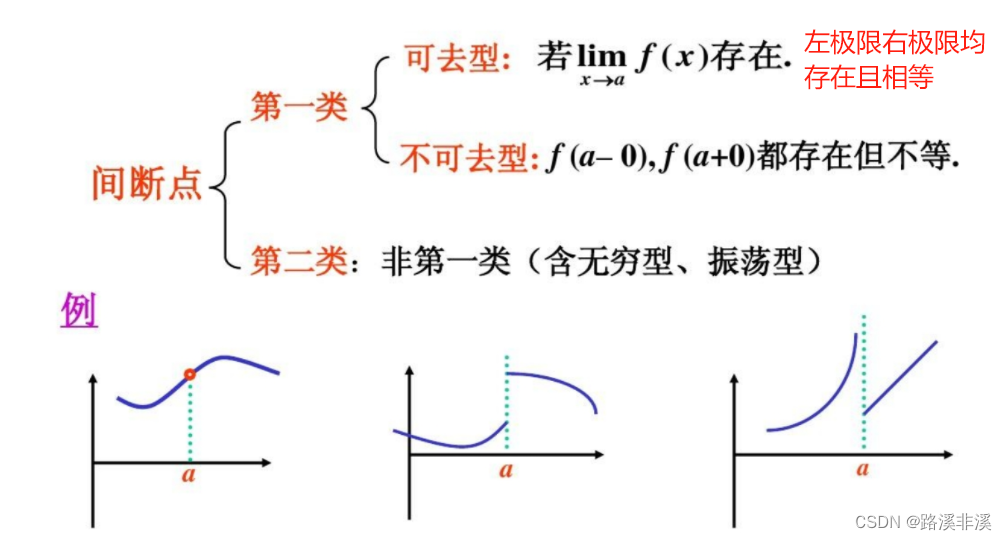
间断点的分类

举例说明

闭区间上连续函数的性质

注意，是闭区间上，并且函数是连续的。

1

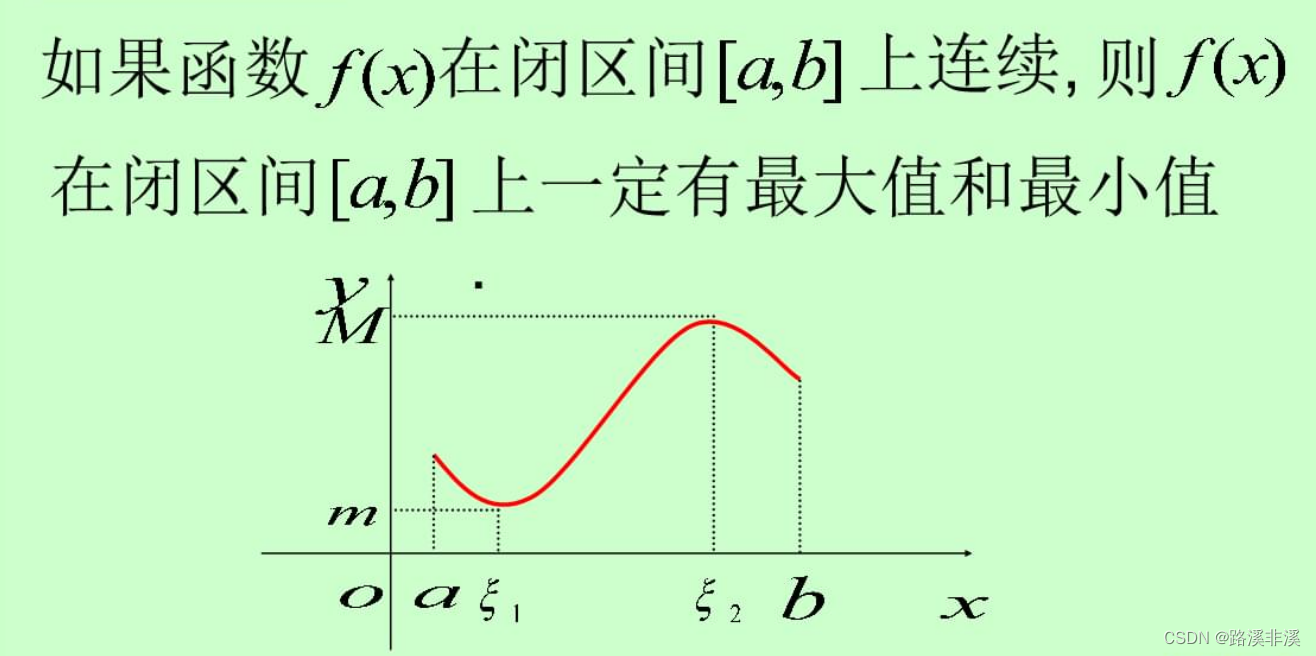
最大最小值定理

对于定理1来说，闭区间且连续，则一定会围成一个范围，则必定在该区间上有界，且一定有最大最小值；

2

零点定理

对于定理2来说，结合坐标系就很好理解，一个连续函数从x下方贯穿到x轴上方，则必定会跟x轴有至少1个交点；

零点定理的一个重要应用就是证明方程的根的存在性。

比如

3

介值定理

可以看下面的这张示意图，加深理解