1.31
1.线段树
2.Bad Hair Day S(单调栈)
3.01迷宫(BFS连通块问题+剪枝)(连通性问题的并查集解法)
4.健康的荷斯坦奶牛 Healthy Holsteins(DFS)
线段树与树状数组
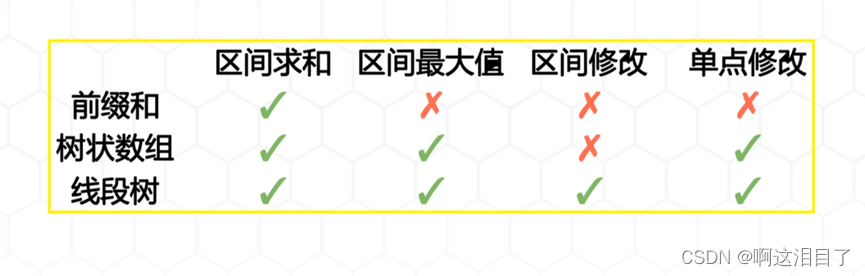
线段树和树状数组的功能相似,但是线段树的功能要更加强大一些,但是线段树的构造比树状数组更加复杂。
在动态区间和的问题上,朴素暴力的算法复杂度达到了O(n^2)效率很低,在前缀和中,计算出所有的前缀和的复杂度是O(n),而查询只要O(1),所以总复杂度只有O(n),但如果面对的是动态的区间和问题,计算量就会大大增加,如果涉及到区间修改,就会更加棘手,因为修改其中的一个值,会导致后面的前缀和发生改变,所以就需要O(n)的复杂度,那么如果改变m次元素的值,复杂度就达到了O(mn),和暴力的方法是一样的,所以就需要用到树状数组或者是线段树这样的结构,由于这样的结构存储是非线性的,所以在修改元素上的时间是O(logn),同理查询某个元素的复杂度也是O(logn),由于初始化数组的时候,需要逐个读取数值所以初始化的复杂度是O(nlogn)所以总复杂度是O(nlogn),线段树的复杂度和树状数组是相当的,线段树和树状数组的区别就在于树状数组在面对区间查询,区间修改问题时非常棘手,而线段树可以很轻松的解决区间问题
树状数组主要就只有三个函数,lowbit(),更新函数:update(),求和函数:sum()
#define lowbit(x) (x& (-x))void update(int x,int k)
{while(x<=n){tree[x]+=k;x+=lowbit(x);//子节点+k,父节点都要+k }
}int sum(int x)
{int res=0;while (x>0){res+=tree[x];x-=lowbit(x);//求的是1---x的区间和 }return res;
}这三个函数构成了树状数组的主要部分
初始化数组
for (int i=1;i<=n;++i){cin>>a[i];update(i,a[i]);}全部代码(单点修改+区间查询)https://www.luogu.com.cn/problem/P3374
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
#define lowbit(x) (x& (-x))
int tree[N],a[N];
int n;
void update(int x,int k)
{while(x<=n){tree[x]+=k;x+=lowbit(x);//子节点+k,父节点都要+k }
}
int sum(int x)
{int res=0;while (x>0){res+=tree[x];x-=lowbit(x);//求的是1---x的区间和 }return res;
}
signed main()
{int q;cin>>n>>q;for (int i=1;i<=n;++i){cin>>a[i];update(i,a[i]);}for (int i=0;i<q;++i){int a,b,c;cin>>a>>b>>c;if (a==1){update(b,c);}else if (a==2){int ans=0;ans=sum(c)-sum(b-1);cout<<ans<<endl;}}
}(区间修改+单点查询)需要用到差分数组的性质https://www.luogu.com.cn/problem/P3368
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
#define lowbit(x) (x& (-x))
int tree[N],a[N],d[N];
int n,q;
void update(int x,int k)
{while (x<=n){tree[x]+=k;x+=lowbit(x);}
}
int sum(int x)
{int res=0;while (x>0){res+=tree[x];x-=lowbit(x);}return res;
}
signed main()
{cin>>n>>q;for (int i=1;i<=n;++i){cin>>a[i];d[i]=a[i]-a[i-1];update(i,d[i]);//放的是差分数组的值,这样树状数组保存的就是差分数组的前缀和 }for (int i=0;i<q;++i){int op;cin>>op;if (op==1){int a,b,c;cin>>a>>b>>c;update(a,c);update(b+1,-c);}if (op==2){int a;cin>>a;int res=sum(a);cout<<res<<endl;}}}运用线段树会麻烦很多
它需要向上更新函数push_up,向下更新函数push_down,建树函数build,更新函数update和查询函数query
同时树上的节点都是以结构体的形式出现,这样方便找到当前节点的区间
struct node{int sum;int l;int r;int add;
}tree[4*N];
int a[N];inline void push_up(int p){tree[p].sum=tree[lc].sum+tree[rc].sum;
}
inline void push_down(int p){if (tree[p].add){tree[lc].sum+=tree[p].add*(tree[lc].r-tree[lc].l+1);tree[lc].add+=tree[p].add;tree[rc].sum+=tree[p].add*(tree[rc].r-tree[rc].l+1);tree[rc].add+=tree[p].add;tree[p].add=0;}return ;
}
inline void build(int p,int l,int r){tree[p]={a[l],l,r,0};if (l==r) return ;int mid=tree[p].l+tree[p].r>>1;build(lc,l,mid);build(rc,mid+1,r);push_up(p);
}
inline void update(int p,int l,int r,int k){if (tree[p].l>=l && tree[p].r<=r){tree[p].sum+=k*(tree[p].r-tree[p].l+1);tree[p].add+=k;return ;}push_down(p);int mid=tree[p].r+tree[p].l>>1;if (mid>=l) update(lc,l,r,k);if (mid<r) update(rc,l,r,k);push_up(p);
}
inline int query(int p,int l,int r){if (tree[p].l>=l && tree[p].r<=r){return tree[p].sum;}push_down(p);int mid=tree[p].l+tree[p].r>>1;int s=0;if (mid>=l) s+=query(lc,l,r);if (mid<r) s+=query(rc,l,r);return s;
}但是打好框架之后解决问题就很简单。只需要改改数值就好了
单点修改+区间查询:https://www.luogu.com.cn/problem/P3374
#include <bits/stdc++.h>
using namespace std;#define int long long
#define lc p<<1
#define rc p<<1|1const int N=1e6+10;
struct node{int sum;int l;int r;int add;
}tree[4*N];
int a[N];
inline void push_up(int p){tree[p].sum=tree[lc].sum+tree[rc].sum;
}
inline void push_down(int p){if (tree[p].add){tree[lc].sum+=tree[p].add*(tree[lc].r-tree[lc].l+1);tree[lc].add+=tree[p].add;tree[rc].sum+=tree[p].add*(tree[rc].r-tree[rc].l+1);tree[rc].add+=tree[p].add;tree[p].add=0;}return ;
}
inline void build(int p,int l,int r){tree[p]={a[l],l,r,0};if (l==r) return ;int mid=tree[p].l+tree[p].r>>1;build(lc,l,mid);build(rc,mid+1,r);push_up(p);
}
inline void update(int p,int l,int r,int k){if (tree[p].l>=l && tree[p].r<=r){tree[p].sum+=k*(tree[p].r-tree[p].l+1);tree[p].add+=k;return ;}push_down(p);int mid=tree[p].r+tree[p].l>>1;if (mid>=l) update(lc,l,r,k);if (mid<r) update(rc,l,r,k);push_up(p);
}
inline int query(int p,int l,int r){if (tree[p].l>=l && tree[p].r<=r){return tree[p].sum;}push_down(p);int mid=tree[p].l+tree[p].r>>1;int s=0;if (mid>=l) s+=query(lc,l,r);if (mid<r) s+=query(rc,l,r);return s;
}
signed main(){int n,m;cin>>n>>m;for (int i=1;i<=n;++i) cin>>a[i];build(1,1,n);for (int i=0;i<m;++i){int op;cin>>op;if (op==1){int a,b;cin>>a>>b;update(1,a,a,b);}else if (op==2){int a,b;cin>>a>>b;int sum1=query(1,a,b);cout<<sum1<<endl;}}
}区间修改+单点查询:https://www.luogu.com.cn/problem/P3368
#include <bits/stdc++.h>
using namespace std;#define int long long
#define lc p<<1
#define rc p<<1|1const int N=1e6+10;
struct node{int sum;int l;int r;int add;
}tree[4*N];
int a[N];
inline void push_up(int p){tree[p].sum=tree[lc].sum+tree[rc].sum;
}
inline void push_down(int p){if (tree[p].add){tree[lc].sum+=tree[p].add*(tree[lc].r-tree[lc].l+1);tree[lc].add+=tree[p].add;tree[rc].sum+=tree[p].add*(tree[rc].r-tree[rc].l+1);tree[rc].add+=tree[p].add;tree[p].add=0;}return ;
}
inline void build(int p,int l,int r){tree[p]={a[l],l,r,0};if (l==r) return ;int mid=tree[p].l+tree[p].r>>1;build(lc,l,mid);build(rc,mid+1,r);push_up(p);
}
inline void update(int p,int l,int r,int k){if (tree[p].l>=l && tree[p].r<=r){tree[p].sum+=k*(tree[p].r-tree[p].l+1);tree[p].add+=k;return ;}push_down(p);int mid=tree[p].r+tree[p].l>>1;if (mid>=l) update(lc,l,r,k);if (mid<r) update(rc,l,r,k);push_up(p);
}
inline int query(int p,int l,int r){if (tree[p].l>=l && tree[p].r<=r){return tree[p].sum;}push_down(p);int mid=tree[p].l+tree[p].r>>1;int s=0;if (mid>=l) s+=query(lc,l,r);if (mid<r) s+=query(rc,l,r);return s;
}
signed main(){int n,m;cin>>n>>m;for (int i=1;i<=n;++i) cin>>a[i];build(1,1,n);for (int i=0;i<m;++i){int op;cin>>op;if (op==1){int a,b,c;cin>>a>>b>>c;update(1,a,b,c);}else if (op==2){int a;cin>>a;int sum1=query(1,a,a);cout<<sum1<<endl;}}
}区间修改,区间查询https://www.luogu.com.cn/problem/P3372
#include <bits/stdc++.h>
using namespace std;#define int long long
#define lc p<<1
#define rc p<<1|1const int N=1e6+10;
struct node{int sum;int l;int r;int add;
}tree[4*N];
int a[N];
inline void push_up(int p){tree[p].sum=tree[lc].sum+tree[rc].sum;
}
inline void push_down(int p){if (tree[p].add){tree[lc].sum+=tree[p].add*(tree[lc].r-tree[lc].l+1);tree[lc].add+=tree[p].add;tree[rc].sum+=tree[p].add*(tree[rc].r-tree[rc].l+1);tree[rc].add+=tree[p].add;tree[p].add=0;}return ;
}
inline void build(int p,int l,int r){tree[p]={a[l],l,r,0};if (l==r) return ;int mid=tree[p].l+tree[p].r>>1;build(lc,l,mid);build(rc,mid+1,r);push_up(p);
}
inline void update(int p,int l,int r,int k){if (tree[p].l>=l && tree[p].r<=r){tree[p].sum+=k*(tree[p].r-tree[p].l+1);tree[p].add+=k;return ;}push_down(p);int mid=tree[p].r+tree[p].l>>1;if (mid>=l) update(lc,l,r,k);if (mid<r) update(rc,l,r,k);push_up(p);
}
inline int query(int p,int l,int r){if (tree[p].l>=l && tree[p].r<=r){return tree[p].sum;}push_down(p);int mid=tree[p].l+tree[p].r>>1;int s=0;if (mid>=l) s+=query(lc,l,r);if (mid<r) s+=query(rc,l,r);return s;
}
signed main(){int n,m;cin>>n>>m;for (int i=1;i<=n;++i) cin>>a[i];build(1,1,n);for (int i=0;i<m;++i){int op;cin>>op;if (op==1){int a,b,c;cin>>a>>b>>c;update(1,a,b,c);}else if (op==2){int a,b;cin>>a>>b;int sum1=query(1,a,b);cout<<sum1<<endl;}}
}Bad Hair Day Shttps://www.luogu.com.cn/problem/P2866
题目描述
农夫约翰有 �N 头奶牛正在过乱头发节。
每一头牛都站在同一排面朝右,它们被从左到右依次编号为 1,2,⋯ ,�1,2,⋯,N。编号为 �i 的牛身高为 ℎ�hi。第 �N 头牛在最前面,而第 11 头牛在最后面。
对于第 �i 头牛前面的第 �j 头牛,如果 ℎ�>ℎ�+1,ℎ�>ℎ�+2,⋯ ,ℎ�>ℎ�hi>hi+1,hi>hi+2,⋯,hi>hj,那么认为第 �i 头牛可以看到第 �+1i+1 到第 �j 头牛。
定义 ��Ci 为第 �i 头牛所能看到的牛的数量。请帮助农夫约翰求出 �1+�2+⋯+��C1+C2+⋯+CN。
输入格式
输入共 �+1N+1 行。
第一行为一个整数 �N,代表牛的个数。
接下来 �N 行,每行一个整数 ��ai,分别代表第 1,2,⋯ ,�1,2,⋯,N 头牛的身高。
输出格式
输出共一行一个整数,代表 �1+�2+⋯+��C1+C2+⋯+CN。
输入输出样例
输入 #1复制
6 10 3 7 4 12 2
输出 #1复制
5
说明/提示
数据规模与约定
对于 100%100% 的数据,保证 1≤�≤8×1041≤N≤8×104,1≤ℎ�≤1091≤hi≤109。
思路:单调栈,单调减的栈,栈空时入栈,遇到比栈顶大的元素时出栈直到栈空或者栈顶栈顶元素更大,10入栈前,栈内没有元素,所以计数器+0,入栈,3比10小,入栈前计数器+1(栈的长度)由于7的长度大于3,所以3出栈,计数器+1,7入栈,4比7小,计数器+2,4入栈......
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int N=8e4+5;
int h[N];
stack<int>st;
signed main(){int n;cin>>n;int sum=0;for (int i=1;i<=n;++i)cin>>h[i];for (int i=1;i<=n;++i){while (!st.empty() && h[st.top()]<=h[i]){st.pop();}sum+=st.size();st.push(i);}cout<<sum;
}01迷宫
题目描述
有一个仅由数字 00 与 11 组成的 �×�n×n 格迷宫。若你位于一格 00 上,那么你可以移动到相邻 44 格中的某一格 11 上,同样若你位于一格 11 上,那么你可以移动到相邻 44 格中的某一格 00 上。
你的任务是:对于给定的迷宫,询问从某一格开始能移动到多少个格子(包含自身)。
输入格式
第一行为两个正整数 �,�n,m。
下面 �n 行,每行 �n 个字符,字符只可能是 00 或者 11,字符之间没有空格。
接下来 �m 行,每行两个用空格分隔的正整数 �,�i,j,对应了迷宫中第 �i 行第 �j 列的一个格子,询问从这一格开始能移动到多少格。
输出格式
�m 行,对于每个询问输出相应答案。
输入输出样例
输入 #1复制
2 2 01 10 1 1 2 2
输出 #1复制
4 4
说明/提示
对于样例,所有格子互相可达。
- 对于 20%20% 的数据,�≤10n≤10;
- 对于 40%40% 的数据,�≤50n≤50;
- 对于 50%50% 的数据,�≤5m≤5;
- 对于 60%60% 的数据,�,�≤100n,m≤100;
- 对于 100%100% 的数据,1≤�≤10001≤n≤1000,1≤�≤1000001≤m≤100000。
思路:连通块问题,用搜索和并查集都可以
用 BFS的时候记得判重,不然会TLE
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define check(tx,ty) (tx>=1 && ty >=1 && tx<=n && ty<= n)
const int N=1005;
int vis[N][N],a[N][N];
struct node{int x;int y;
}q[1000001];
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int step[N][N];
signed main(){int n,m;cin>>n>>m;for (int i=1;i<=n;++i){for (int j=1;j<=n;++j){scanf("%1d",&a[i][j]);}}for (int i=0;i<m;++i){int sx,sy,tail=0,head=0;int cnt=1;cin>>sx>>sy;if (step[sx][sy]!=0){cout<<step[sx][sy]<<endl;continue;}q[tail].x=sx,q[tail].y=sy;step[sx][sy]=1;tail++;while (head<tail){int x=q[head].x,y=q[head].y;for (int i=0;i<4;++i){int tx=x+dir[i][0],ty=y+dir[i][1];if (check(tx,ty) && step[tx][ty]==0 && a[tx][ty]!=a[x][y]){q[tail].x=tx,q[tail].y=ty;step[tx][ty]=1;tail++;cnt++;}}head++;}for (int i=0;i<tail;++i){step[q[i].x][q[i].y]=cnt;}printf("%d\n",cnt);}
}下面是并查集做法
遍历所有的点,如果两个点连通但未合并,那就合并
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
#define check(tx,ty) (tx>=1 && ty >=1 && tx<=n && ty<= n)
const int N=1005;
int f[N*N];
int cnt[N*N];
int aa[N][N];
int dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int find(int x){if (f[x]==x)return x;else{f[x]=find(f[x]);return f[x];}
}
void unionn(int i,int j){f[find(i)]=find(j);
}
signed main(){int m,n;cin>>n>>m;//初始化并查集for (int i=1;i<=n*n;++i){f[i]=i;cnt[i]=1;}for (int i=1;i<=n;++i){for (int j=1;j<=n;++j){scanf("%1d",&aa[i][j]);}}for (int i=1;i<=n;++i){for (int j=1;j<=n;++j){for (int k=0;k<4;++k){int a=i+dir[k][0],b=j+dir[k][1];if (a>=1 && a<=n && b>=1 && b<=n){if (aa[i][j]!=aa[a][b]){int x=find((i-1)*n+j);int y=find((a-1)*n+b);if (x!=y){unionn(x,y);cnt[y]+=cnt[x]; }}}}}}while (m--){int sx,sy;cin>>sx>>sy;cout<<cnt[find((sx-1)*n+sy)]<<endl;}
}健康的荷斯坦奶牛 Healthy Holsteinshttps://www.luogu.com.cn/problem/P1460
题目描述
农民 John 以拥有世界上最健康的奶牛为傲。他知道每种饲料中所包含的牛所需的最低的维他命量是多少。请你帮助农夫喂养他的牛,以保持它们的健康,使喂给牛的饲料的种数最少。
给出牛所需的最低的维他命量,输出喂给牛需要哪些种类的饲料,且所需的饲料剂量最少。
维他命量以整数表示,每种饲料最多只能对牛使用一次,数据保证存在解。
输入格式
第一行一个整数 �v,表示需要的维他命的种类数。
第二行 �v 个整数,表示牛每天需要的每种维他命的最小量。
第三行一个整数 �g,表示可用来喂牛的饲料的种数。
下面 �g 行,第 �n 行表示编号为 �n 饲料包含的各种维他命的量的多少。
输出格式
输出文件只有一行,包括牛必需的最小的饲料种数 �p;后面有 �p 个数,表示所选择的饲料编号(按从小到大排列)。
如果有多个解,输出饲料序号最小的(即字典序最小)。
输入输出样例
输入 #1复制
4 100 200 300 400 3 50 50 50 50 200 300 200 300 900 150 389 399
输出 #1复制
2 1 3
说明/提示
【数据范围】
对于 100%100% 的数据,1≤�≤251≤v≤25,1≤�≤151≤g≤15。
输入的所有整数在 [1,1000][1,1000] 范围内。
思路:DFS排列问题
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x& - (x))
#define int long long
const int N=1000;
int v[N],g[N][N],ans[N],c[N];
int m,n,minx=100000000;
bool check(int x){for (int i=1;i<=n;++i){int sum=0;for (int j=1;j<=x;++j){sum+=g[c[j]][i];}if (sum<v[i])return false;}return true;
}
void dfs(int t , int s){if (s>minx) return ;if (t>m){ if (check(s)){if (s<minx){minx=s;for (int i=1;i<=minx;++i){ans[i]=c[i];}}}return ;}c[s+1]=t;dfs(t+1,s+1);c[s+1]=0;dfs(t+1,s);
}
signed main(){cin>>n;for (int i=1;i<=n;++i) cin>>v[i];cin>>m;for (int i=1;i<=m;++i){for (int j=1;j<=n;++j){cin>>g[i][j];}}dfs(1,0);cout<<minx<<" ";for (int i=1;i<=minx;++i){cout<<ans[i]<<" ";}
}