Brick Wall(Problem - A - Codeforces)
题目大意:规定砖的大小为1*k(k>=2),现在有一面n*m的砖墙,n是墙高,m是墙宽,砖在砖墙中有两种放法,水平放置和竖直放置,墙的稳定性=水平放置的砖的数量-竖直放置的砖的数量。现在要求墙的稳定性的最大值。注意墙不用填满,砖不能相交。
思路:很显然我们尽可能地水平放置,不竖直放置即可。反正又不用填满。
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;scanf("%d",&t);while(t--){int n,m;scanf("%d%d",&n,&m);m /= 2;n*=m;printf("%d\n",n);}
}Minimize Inversions(Problem - B - Codeforces)
题目大意:现在有两个排列a,b,我们需要选择两个位置i,j,交换ai,aj和bi,bj,最后要使两个序列中的反转数最小。
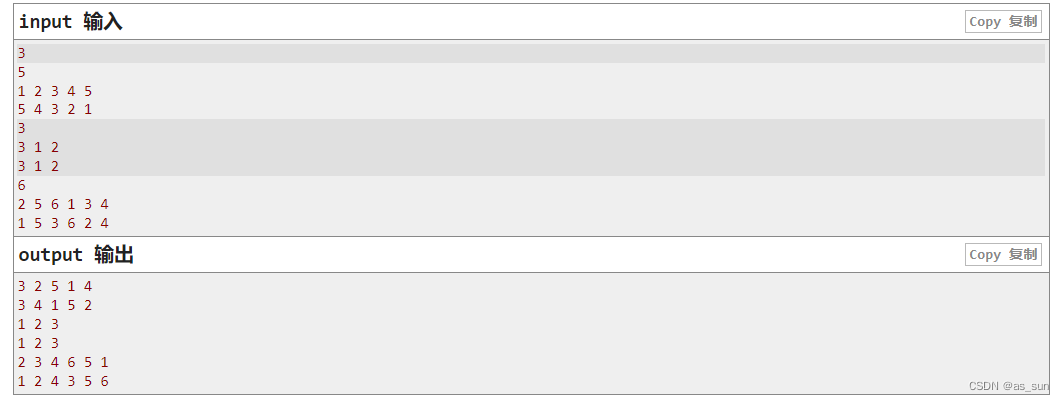
思路:刚开始我看到这个题也没有什么头绪,然后就去分析了下样例,前两个样例没什么感觉,看到第三个样例的时候,我突然发现第三个样例的输出中第二个排列有序的。呀,昨晚上太着急了,以为它们是有序的,刚刚一看竟然不是,但是最后的结果确实是使一个排序变成有序的。不过我们还是来证明一下比较放心。
我们很容易通过交换使一个排列变成有序的,这样的话,两个排列中的反转数会是最小的吗?显然在有序的那个排列中反转数为0,那么在另一个序列中呢?哎,这个有点证不明白,但是写题解还是不要水,我去看了下官方的证明,思路大概是这样:
对于a,b我们选出来的i,j构成的逆序对数量为0,1,2,如果其中一个排列有序,那么另一个最多是1,这样对于这一对来说就是最优解,让某个序列全部排序,那么每一对都是最优的情况,那么就是最小的时候。
#include<bits/stdc++.h>
using namespace std;
int a[200010],b[200010];
int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);vector<pair<int,int>>p;for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) scanf("%d",&b[i]);for(int i=1;i<=n;i++) p.push_back({a[i],b[i]});sort(p.begin(),p.end());for(int i=0;i<n;i++){int x=p[i].first,y=p[i].second;printf("%d ",x);}printf("\n");for(int i=0;i<n;i++){int x=p[i].first,y=p[i].second;printf("%d ",y);}printf("\n");}
}XOR-distance(Problem - C - Codeforces)
题目大意:现有三个数a,b,r,我们需要在[0,r]中选一个数x,使得|(a^x)-(b^x)|最小,输出最小值。
思路:既然涉及到位运算,那么我们就从二进制的角度来看:
显然如果a,b在二进制的某一位相同,那么和x进行异或之后,还是相同的,所以没什么变化,那么我们要想最小化结果,肯定还是要从不同位入手,很明显如果一个为0,一个为1,那么如果是0作为被减数,那么就要从高位退1下来参与,所以我们肯定将最高位1在的那个数中二进制下为1,而另一个数二进制下为0的位置更改一下,另外第一个相异的位置不能改动,因为要从这里退位下来。那么问题就解决了。那么我们直接进行位运算即可,注意不要超过r。
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{int t;scanf("%lld",&t);while(t--){int a,b,r;scanf("%lld%lld%lld",&a,&b,&r);if(a<b) swap(a,b);int flag=1;for(int i=60;i>=0;i--){int ta=(a>>i)&1,tb=(b>>i)&1;if(flag&&ta!=tb) {flag=0;continue;}if(!flag){if(ta==1&&tb==0) {if((1ll<<i)<=r) {r -= (1ll<<i);a ^= (1ll<<i);b ^= (1ll<<i);}}}}cout<<abs(a-b)<<endl;}
}Blocking Elements(Problem - D - Codeforces)
题目大意:现在有一个数组a[]和一个数组b[],我们要在a[]中将a[b[i]]的位置挑出来相加,剩下的以被挑走的位置为分隔,划出若干个区间,每个区间内部求和,这些和中的最大值作为结果,输出最小结果。举个例子:
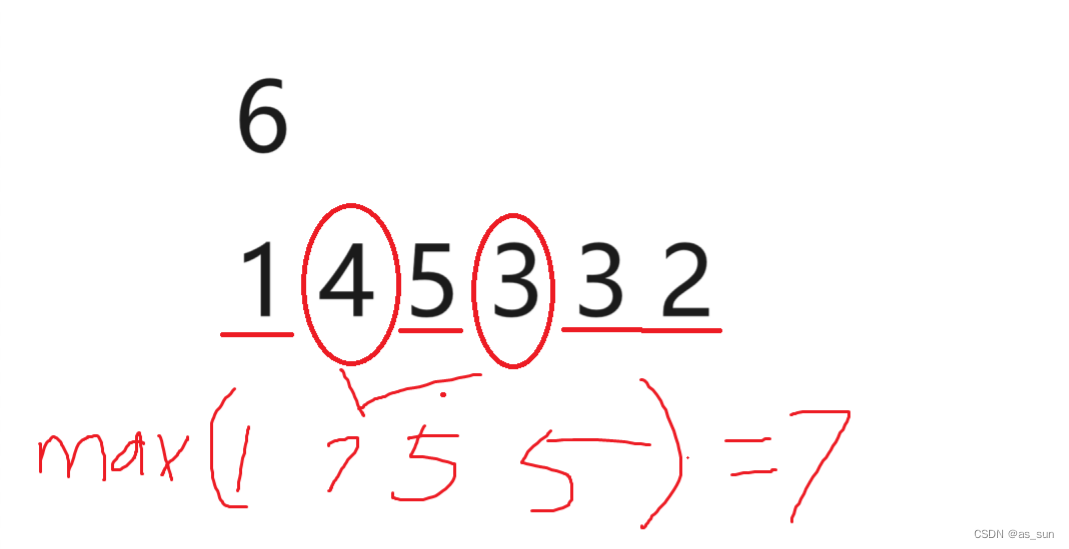
思路:这里的结果肯定是在[1,sum]之内,所以想到二分,要快速求若干区间的和,那么想到预处理前缀和。现在最关键的问题就是二分的check函数怎么写。
我最初想的是就从头开始,一旦超过mid之后就以此划分,最后看挑出来的数是否小于mid,但是显然这个思路不可以。这么来看,我们第一次划分前的所有位置实际都可以作为第一次划分的位置,当然第二,第三次划分也是同理,那么就跟dfs联系起来了,对于搜每一次划分的位置。但是,显然时间复杂度太高了,这个题n的范围还有点大,那么就得换个思路。dfs简化就很容易想到动态规划,那么我们该如何动态规划呢?其实这里已经分析出了一个很重要的条件,每次划分的合法位置是一个区间,那么我们要想使结果最优,肯定是从这个区间中挑比较小的数加进结果。那么可以定义dp[i]表示以i位置为区间结尾,此时被挑选的数的和。因为我们在挑选的时候已经确定了每个区间的和是小于m的,进而来找划分位置,所以只要从这些合法的中找一个最小的即可。从一个区间中找最值,很容易想到滑动窗口,这里又是dp,那么就是单调队列优化dp的类型。还有一个问题,找合法区间的左端点时,是否必须从头开始找,显然不是,因为很容易可以发现,如果当前的i的左端点在j位置,那么后一个i的左端点一定是在j位置后面,因为我们确定区间只是通过区间和小于m来确定的。每一个值都是正数,那么区间和,区间一定不会再变长。所以我们只用看队列的开头是否需要弹出,来找合适的位置,因为队列是单增的,所以开头一定最小。
另外,结尾可能在任意位置,所以我们要循环判断一下。
#include<bits/stdc++.h>
using namespace std;
#define int long long
int q[100010],a[100010],s[100010],dp[100010],hh,tt,n;
int check(int m)
{hh=0,tt=1;//数组模拟队列q[0]=0;for(int i=1;i<=n;i++){while(hh<tt&&s[i-1]-s[q[hh]]>m) hh++;dp[i]=dp[q[hh]]+a[i];while(hh<tt&&dp[q[tt-1]]>=dp[i]) tt--;q[tt++]=i;}for(int i=1;i<=n;i++)if(dp[i]<=m&&s[n]-s[i]<=m) return 1;return 0;
}
signed main()
{int t;scanf("%lld",&t);while(t--){scanf("%lld",&n);for(int i=1;i<=n;i++) scanf("%lld",&a[i]),s[i]=s[i-1]+a[i];int l=1,r=s[n];while(l<r){int mid=(l+r)/2;if(check(mid)) r=mid;else l=mid+1;}printf("%lld\n",l);}
}核心:虽然这道题既有区间和又有选点,但本质上考的是在限制区间的情况下求最小值,限制区间的条件比较隐蔽而已。 因为每一个划分的合法位置实际在一个区间中找,那么显然要找最小值,那么就是区间找最小值的问题,然后有多个位置,所以联系到单调队列优化的dp问题。