目录
1、基本概念
2、二叉树Binary Tree
3、树、森林与二叉树的转换
4、赫夫曼树Huffman Tree与赫夫曼编码Huffman Coding
1、基本概念
(1)树(Tree)是 n(n ≥\geq 1)个节点的有限集,n = 0时称为空树。
(2)非空树唯一拥有一个根(Root)结点(Node),n > 1时其余结点可分为m(m > 0)个互不相交的有限集并各自成根的子树(Sub Tree)。
(3)结点拥有的子树数目称为结点的度(Degree),度为 0 的结点称为叶结点(Leaf),树的度是树各结点的度的最大值。

(4)结点之间的关系:兄弟(Sibling)——孩子(Child)——双亲(Parent)

(5)结点的层次(Level)从根算起,根为第一层,根的孩子为第二层一直往下,最大层次为深度(Depth)。

(6)如果将树中结点的各子树看成从左至右呈有次序的不能互换的,则称该树为有序树,否则称为无序树。
(7)森林(Forest)是 m(m ≥\geq 0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
(8)树的双亲表示法如下,data数据域存储结点的数据信息;parent指针域存储该结点双亲在数组中的下标,根结点的parent定义为 -1 即不存在该结点。

2、二叉树Binary Tree
(1)每个结点的度 ≤\leq 2,左右有次序之分的树称为二叉树。
(2)二叉树的五种基本形态:空二叉树、只有一个根结点、根结点只有左子树、根结点只有右子树、根结点既有左子树又有右子树。
(3)斜树包含左斜树(所有结点都只有左子树的二叉树)和右斜树(所有结点都只有右子树的二叉树),每一层都只有一个结点,结点个数即二叉斜树的深度(同线性表结构)。
(4)满二叉树:叶结点仅在最下层,非叶非根的结点度数均为 2 的二叉树。

满二叉树
(5)完全二叉树:按层序从上到下从左到右编号结点的位置与满二叉树相同的二叉树,特点有叶结点仅在最下两层,最下层叶子集中在左部连续位置,同结点数的二叉树深度最小。

完全二叉树
(6)二叉树的数学性质有:
(i) 第 i 层至多 2i−12^{i-1} 个结点(i ≥\geq 1)
(ii) 深度为k时至多有 2k2^{k} -1个结点(k ≥\geq1)
(iii) 所有节点的度数之和等于节点总数-1,若叶子结点数为 n0n_{0} ,度为2的结点数为n1n_{1} ,则n0n_{0} = n1n_{1} + 1( 二叉树除了叶结点就是度为1或2的结点)
(iv) 具有n个结点的完全二叉树的深度为[logn]+1
(7)顺序存储结构:一般只用于完全二叉树。
(8)二叉链表:一个数据域+两个指针域。
(9)遍历二叉树:从根节点出发,按某种次序依次唯一地访问每个结点。
(i) 前序遍历:若二叉树为空,则空操作返回,否则先访问根结点,然后遍历左子树, 再遍历右子树。
(i) 中序遍历:若二叉树为空,则空操作返回,否则先遍历左子树,然后访问根结点,再遍历右子树。
(i) 后序遍历:若二叉树为空,则空操作返回,否则从左到右先叶子后结点遍历访问左右子树,最后根结点。

(i) 层序遍历:若二叉树为空,则空操作返回,否则从第一层根结点开始往下从左到右对结点逐个访问。
已知前 + 中序 / 中 + 后序遍历序列,都可以唯一确定一棵二叉树。
3、树、森林与二叉树的转换
(1)树转换为二叉树
(i) 加线;在所有兄弟结点之间加一条连线。
(ii) 去线;每个结点只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
(iii) 层次调整:以树的根结点为轴心,将整棵树顺时针旋转一定角度使其结构层次分明。

(2)森林转二叉树
(i) 将每棵树转换为二叉树。
(ii) 第一棵二叉树不动,从第二棵开始依次把后一棵二叉树的根结点作为前一棵根结点的右孩子,连线。

(3)二叉树转换成树
(i) 加线;左孩子的n个右孩子结点都作为此结点的孩子。将该结点与这些右孩子结点用线连接起来。
(ii) 去线;删除原二叉树中所有结点与其右孩子结点的连线。

(4)二叉树转森林
(i) 从根结点开始,若存在右孩子,则删除与右孩子的连线。
(ii) 再查看分离后的二叉树,若存在右孩子,则连线删除,直到所有右孩子连线删除为止。
(iii) 再将分离的二叉树都转换为树即可。

4、赫夫曼树Huffman Tree与赫夫曼编码Huffman Coding
从树一个结点到另一个结点的之间的分支构成两个结点之间的路径,路径分支数目称为路径长度。树的路径长度即从树根到每一结点的路径长度之和,结点间连线相关数称为权(Weight)。树的带权路径长度为树中所有叶子结点的带权路径长度之和,带权路径长度WPL最小的二叉树称为赫夫曼树。

二叉树a的路径长度为1+1+2+2+3+3+4+4=20,WPL = 5×\times1 + 15×\times2 + 40×\times3 + 30×\times4 + 10×\times4 = 315
二叉树b的路径长度为1+2+3+3+2+1+2+2=16,WPL = 5×\times3 +15×\times3 + 40×\times2 + 30×\times2 + 10×\times4 = 220
我们可以得出构造赫夫曼树的算法描述:
(1)根据给定的n个权值{ w1w_{1},w2w_{2},w3w_{3}……,wnw_{n}},构成 n 棵二叉树的集合F={ T1T_{1},T2T_{2},T3T_{3}……,TnT_{n}},其中每棵二叉树T中只有一个带权为w的根结点,其左右子树均为空。
(2)在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,并置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
(3)在 F 中删除这两棵树,同时将新得到的二叉树加入F中。
(4)重复步骤(2)和(3)直到F只含一棵树为止,这棵树便是赫夫曼树。
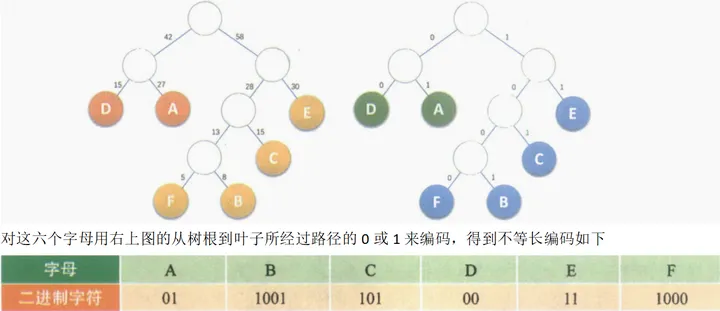
赫夫曼编码:规定赫夫曼树的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,即赫夫曼编码,它在信息存储与传输过程中对信息高效压缩。
假设六个字母的频率为A 27,B 8,C 15,D 15,E 30,F 5,合起来正好是100%,赫夫曼树构造如下: