本章全篇参考赵世钰老师的教材 Mathmatical-Foundation-of-Reinforcement-Learning Policy Gradient Methods 章节，请各位结合阅读，本合集只专注于数学概念的代码实现。

Average state value

对所有状态值的加权平均
$$\begin{array}{rl}\bar{v}=& \sum _{s\in S}{v}_{\pi }(s)\\ =& E_{S-d}(v_{\pi }(S))\\ =& E_{S-d}(\sum _{a\in A}q(s,a)\pi (a|s))\end{array}$$

策略函数为$\pi (a|s,\theta )$
令$J(\theta )=\bar{v}$
对其求梯度

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )=& E_{S-d}(\sum _{a\in A}q(s,a){\nabla }_{\theta }\pi (a|s,\theta ))\\ =& E_{S-d}(\sum _{a\in A}q(s,a)\pi (a|s,\theta ){\nabla }_{\theta }ln\pi (a|s,\theta ))\\ =& E_{S-d}[E_{a-\pi (S,\Theta )}[q(s,a){\nabla }_{\theta }ln\pi (a|s,\theta )]]\\ =& E_{S-d,a-\pi (S,\Theta )}[q(s,a){\nabla }_{\theta }ln\pi (a|s,\theta )]\end{array}$$

Average reward

$$\bar{r}=(1-\gamma )\bar{v}$$

Monte Carlo policy gradient (REINFORCE)

为了求$max\bar{v}=max{J}_{\theta }$ ，则

$${\theta }_{t+1}={\theta }_t+{\nabla }_{\theta }J({\theta }_t)$$

REINFORCE示例

$$\begin{array}{rl}{\theta }_{t+1}=& {\theta }_t+{\nabla }_{\theta }J({\theta }_t)\\ =& {\theta }_t+{\nabla }_{\theta }{E}_{S-d,a-\pi (S,\Theta )}[q(s,a){\nabla }_{\theta }ln\pi (a|s,\theta )]\end{array}$$
一般来说，${\nabla }_{\theta }ln\pi (a|s,\theta )$是未知的，可以用随机梯度法来估计，则
$$\begin{array}{rl}{\theta }_{t+1}=& {\theta }_t+{\nabla }_{\theta }J({\theta }_t)\\ =& {\theta }_t+{\nabla }_{\theta }[q(s,a){\nabla }_{\theta }ln\pi (a|s,\theta )]\end{array}$$

在torch里面编写这段代码

• 1、用随机权重初始化策略网络
• 2、运行N个完整的片段，保存其(s,a,r,s’)状态转移
• 3、对于每个片段k的每一步t，计算后续步的带折扣的总奖励$Q_{k,t}={\sum }_{i=0}{\gamma }_i{r}_i$
• 4、计算所有状态转移的损失函数 $L=-{\sum }_{k,t}{Q}_{k,t}ln\pi (a_{k,t}|s_{k,t})$，由于torch自带的是梯度下降，所以带个负号更新，sum为小批量
• 5、执行SGD更新权重，以最小化损失
• 6、从步骤2开始重复，直到收敛

1、用随机权重初始化策略网络

import collections
import copy
import math
import random
import time
from collections import defaultdictimport gym
import gym.spaces
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from gym.envs.toy_text import frozen_lake
from torch.utils.tensorboard import SummaryWriter# 1、用随机权重初始化策略网络
class PolicyNet(nn.Module):def __init__(self, obs_n, hidden_num, act_n):super().__init__()# 动作优势A(s, a)self.net = nn.Sequential(nn.Linear(obs_n, hidden_num),nn.ReLU(),nn.Linear(hidden_num, act_n),nn.Softmax(dim=1),)def forward(self, state):if len(torch.Tensor(state).size()) == 1:state = state.reshape(1, -1)return self.net(state)

2、运行N个完整的片段，保存其(s,a,r,s’)状态转移

def generate_episode(env, n_steps, net, predict=False):episode_history = dict()r_list = []for _ in range(n_steps):episode = []predict_reward = []state, info = env.reset()while True:p = net(torch.Tensor(state)).detach().numpy().reshape(-1)action = np.random.choice(list(range(env.action_space.n)), p=p)next_state, reward, terminated, truncted, info = env.step(action)episode.append([state, action, next_state, reward, terminated])predict_reward.append(reward)state = next_stateif terminated or truncted:episode_history[_] = episoder_list.append(len(episode))episode = []predict_reward = []breakif predict:return np.mean(r_list)return episode_history

3、对于每个片段k的每一步t，计算后续步的带折扣的总奖励

def calculate_t_discount_reward(reward_list, gamma):discount_reward = []total_reward = 0for i in reward_list[::-1]:total_reward = total_reward * gamma + idiscount_reward.append(total_reward)return discount_reward[::-1]

4、计算所有状态转移的损失函数 $L=-{\sum }_{k,t}{Q}_{k,t}ln\pi (a_{k,t}|s_{k,t})$

def loss(batch, gamma):l = 0for episode in batch.values():reward_list = [reward for state, action, next_state, reward, terminated in episode]state = [state for state, action, next_state, reward, terminated in episode]action = [action for state, action, next_state, reward, terminated in episode]qt = calculate_t_discount_reward(reward_list, gamma)pi = net(torch.Tensor(state))pi = pi.gather(dim=1, index=torch.LongTensor(action).reshape(-1, 1))l += -torch.Tensor(qt) @ torch.log(pi)return l/len(batch.values())

5，6、训练

## 初始化环境
env = gym.make("CartPole-v1", max_episode_steps=1000)
# env = gym.make("CartPole-v1", render_mode = "human")state, info = env.reset()obs_n = env.observation_space.shape[0]
hidden_num = 64
act_n = env.action_space.n
net = PolicyNet(obs_n, hidden_num, act_n)# 定义优化器
opt = optim.Adam(net.parameters(), lr=0.01)# 记录
writer = SummaryWriter(log_dir="logs/PolicyGradient/reinforce", comment="test1")epochs = 1000
batch_size = 200
gamma = 0.9for epoch in range(epochs):batch = generate_episode(env, batch_size, net)l = loss(batch, gamma)# 反向传播opt.zero_grad()l.backward()opt.step()writer.add_scalars("Loss", {"loss": l.item(), "max_steps": generate_episode(env, 10, net, predict=True)}, epoch)print("epoch:{},  Loss: {}, max_steps: {}".format(epoch, l.detach(), generate_episode(env, 10, net, predict=True)))

运行结果

这是CartPole-v1的步数提升效果。

改进策略

BaseLine

作为第一个示例，令Q1和Q2都等于某个小的正数，而Q3等于一个大的负数。因此，第一步和第二步的动作得到了一些小的奖励，但是第三步并不是很成功。由这三个步骤所产生的综合梯度将试图使策略远离第三步的动作，而稍微朝第一步和第二步采取的动作靠拢，这是完全合理的。

现在让我们想象一下，假设奖励永远是正的，只有价值不同。这对应于为每个奖励（Q1、Q2和Q3）加上一些常数。在这种情况下，Q1和Q2将变为较大的正数，而Q3为较小的正值。但是，策略更新将有所不同！接下来，我们将努力将策略推向第一步和第二步的动作，并略微将其推向第三步的动作。因此，严格来说，尽管相对奖励是相同的，但我们不再试图避免选择第三步所执行的动作。

策略更新依赖于奖励中所加的常数，这可能会大大减慢训练速度，因为我们可能需要更多样本来平均掉这种策略梯度偏移的影响。甚至更糟的是，由于折扣总奖励随时间变化，随着智能体学着如何表现得越来越好，策略梯度的方差也可能发生变化。

• 1、用随机权重初始化策略网络
• 2、运行N个完整的片段，保存其(s,a,r,s’)状态转移
• 3、对于每个片段k的每一步t，计算后续步的带折扣的总奖励$Q_{k,t}={\sum }_{i\in T}{\gamma }_i{r}_i-\frac{1}{n}{\sum }_{i\in T}{\gamma }_i{r}_i$
• 4、计算所有状态转移的损失函数 $L=-{\sum }_{k,t}{Q}_{k,t}ln\pi (a_{k,t}|s_{k,t})$
• 5、执行SGD更新权重，以最小化损失
• 6、从步骤2开始重复，直到收敛

只需要修改第三步

# 对于每个片段k的每一步t，计算后续步的带折扣的总奖励
def calculate_t_discount_reward(reward_list, gamma, baseline=False):discount_reward = []total_reward = 0for i in reward_list[::-1]:total_reward = total_reward * gamma + iif baseline:discount_reward.append(total_reward - np.mean(reward_list))else:discount_reward.append(total_reward)return discount_reward[::-1]

entropy bonus

即使将策略表示为概率分布，智能体也很有可能会收敛到某些局部最优策略并停止探索环境。在DQN中，我们使用ε-greedy动作选择方式解决了这一问题：有epsilon的概率，智能体执行随机动作，而不是当前策略决定的动作。当然，我们可以使用相同的方法，但是策略梯度方法使我们可以采取更好的方法，即熵奖励（entropy bonus）。

在信息论中，熵是某些系统中不确定性的度量。将熵应用到智能体的策略中，它可以显示智能体对执行何种动作的不确定程度。策略的熵可以用数学符号定义为：H(π) = –∑π(a|s)logπ(a|s)。熵的值始终大于零，并且在策略符合平均分布（换句话说，所有动作具有相同的概率）时具有一个最大值。当策略决定某个动作的概率为1而所有其他动作的概率为0时，熵就变得最小，这意味着该智能体完全确定要做什么。为了防止智能体陷入局部最小值，在损失函数中减去熵，以惩罚智能体过于确定要采取的动作

只需要修改Loss函数。

def loss(batch, gamma, entropy_beta):l = 0for episode in batch.values():reward_list = [reward for state, action, next_state, reward, terminated in episode]state = [state for state, action, next_state, reward, terminated in episode]action = [action for state, action, next_state, reward, terminated in episode]qt = calculate_t_discount_reward(reward_list, gamma)pi = net(torch.Tensor(state))entropy_loss = -torch.sum((pi* torch.log(pi)),axis=1).mean() * entropy_betapi = pi.gather(dim=1, index=torch.LongTensor(action).reshape(-1, 1))l_policy = -torch.Tensor(qt) @ torch.log(pi)l += l_policy - entropy_lossreturn l / len(batch.values())

entropy_beta&baseline

同时加入两种方式，再次修改loss函数

def loss(batch, gamma, entropy_beta=False, baseline=False):l = 0for episode in batch.values():reward_list = [reward for state, action, next_state, reward, terminated in episode]state = [state for state, action, next_state, reward, terminated in episode]action = [action for state, action, next_state, reward, terminated in episode]qt = calculate_t_discount_reward(reward_list, gamma, baseline)pi = net(torch.Tensor(state))entropy_loss = -torch.sum((pi * torch.log(pi)), axis=1).mean() * entropy_betapi = pi.gather(dim=1, index=torch.LongTensor(action).reshape(-1, 1))l_policy = -torch.Tensor(qt) @ torch.log(pi)if entropy_beta:l += l_policy - entropy_losselse:l += l_policyreturn l / len(batch.values())

训练

## 初始化环境
env = gym.make("CartPole-v1", max_episode_steps=200)
# env = gym.make("CartPole-v1", render_mode = "human")state, info = env.reset()obs_n = env.observation_space.shape[0]
hidden_num = 64
act_n = env.action_space.n
net = PolicyNet(obs_n, hidden_num, act_n)# 定义优化器
opt = optim.Adam(net.parameters(), lr=0.01)# 记录
writer = SummaryWriter(log_dir="logs/PolicyGradient/reinforce-entropy-bonus&baseline", comment="test1"
)epochs = 200
batch_size = 20
gamma = 0.9
entropy_beta= 0.01
baseline=Truefor epoch in range(epochs):batch = generate_episode(env, batch_size, net)l = loss(batch, gamma, entropy_beta, baseline)# 反向传播opt.zero_grad()l.backward()opt.step()writer.add_scalars("Loss",{"loss": l.item(), "max_steps": generate_episode(env, 10, net, predict=True)},epoch,)print("epoch:{},  Loss: {}, max_steps: {}".format(epoch, l.detach(), generate_episode(env, 10, net, predict=True)))

对比结果如下

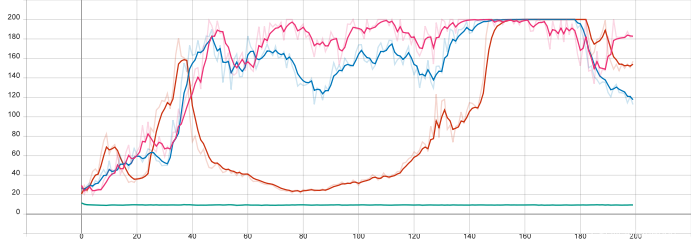
加入entropy_beta可以解决局部最优点问题
baseline可以优化收敛方向。

Ref

[1] Mathematical Foundations of Reinforcement Learning，Shiyu Zhao
[2] 深度学习强化学习实践（第二版），Maxim Lapan