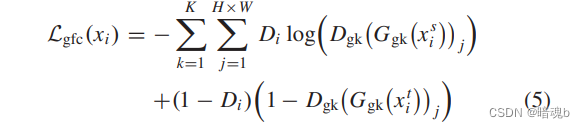1.冒泡排序

思路：比较相邻的两个数字，如果前一个数字大，那么就交换两个数字，直到有序。

• 时间复杂度：O(n^2)，
• 稳定性：这是一种稳定的算法。
  代码实现：

void bubble_sort(int arr[],size_t len){size_t i,j;for(i=0;i<len;i++){	bool hasSwap = false;		//优化，判断数组是否已经有序，如果有序可以提前退出循环for(j=1;j<len-i;j++){		//这里j<len-i是因为最后面的肯定都是最大的，不需要多进行比较if(arr[j-1]>arr[j]){	//如果前一个比后一个大swap(&arr[j-1],&arr[j]);	//交换两个数据hasSwap = true;}	}if(!hasSwap){break;	}}
}

2.插入排序

思路：把一个数字插入一个有序的序列中，使之仍然保持有序，如对于需要我们进行排序的数组，我们可以使它的前i个数字有序，然后再插入i+1个数字，插入到合适的位置使之仍然保持有序，直到所有的数字有序。

• 时间复杂度：O(n^2)
• 稳定性：稳定的算法
  代码实现：

void insert_sort(int arr[],int len)
{int i,j;for(i=1;i<len;i++){int key = arr[i]; //记录当前需要插入的数据for(j= i-1;i>=0&&arr[j]>key;j--){	//找到插入的位置arr[j+1] = arr[j]; //把需要插入的元素后面的元素往后移}arr[j+1] = key;	//插入该元素}
}

3.折半插入排序

思路：本质上是插入排序，但是通过半分查找法找到插入的位置，让效率稍微快一点。

• 时间复杂度：O(n^2)，
• 稳定性：稳定的算法。
  代码实现：

void half_insert_sort(int arr[],int len)
{int i,j;for(i=1;i<len;i++){int key = arr[i];int left = 0;int right = i-1;while(left<=right){	//半分查找找到插入的位置int mid = (left+right)/2;if(key<arr[mid]){right = mid-1;	}else{left = mid+1;	}	}for(j=i-1;j>=left;j--){		//把后面的元素往后移arr[j+1]=arr[j];	}arr[j+1] = key;	//插入元素}
}

4.希尔排序

思路：先取一个正整数d1<n，把所有序号相隔d1的数组元素放一组，组内进行直接插入排序；然后取d2<d1，重复上述分组和排序操作；直至di=1，即所有记录放进一个组中排序为止。

• 时间复杂度：O(n^1.3) ,算法效率上大大提高 。
• 稳定性：不稳定的算法。
• 代码实现

void shell_sort(int arr[],int len)
{	//本质上也是一种插入排序，避免了大量数据的移动，在每一组排序过后，每个数据已经到了大致的位置。int i,j;int step=0;for(step = len/2;step>=1;step=step/2){	//分组  分为step组,对每组的元素进行插入排序for(i=step;i<len;i++){int key = arr[i];for(j=i-step;j>=0&&arr[j]>key;j=j-step){arr[j+step] = arr[j];	}	arr[j+step] = key;}}
}

5.选择排序

思路：通过循环找到最大值所在的位置，然后把最大值和最后一个元素进行交换，通过循环直到所有的数据有序。

• 时间复杂度：O(n^2)
• 稳定性：不稳定的算法
  代码实现：

void select_sort(int arr[],size_t len)
{size_t i,j;for(i=0;i<len-1;i++){int max = 0; //最大值下标for(j=1;j<len-i;j++){if(arr[max]<arr[j]){	//找到最大值的下标max = j;	}	}if(max!=j-1){	swap(&arr[max],&arr[j-1]);	//把最后一个元素和最大值进行交换}}
}

6.鸡尾酒排序

思路：选择排序的一种改进，一次循环直接找到最大值和最小值的位置，把最大值和最后一个元素进行交换，最小值和最前一个元素进行交换，所以最外层的循环只需要执行len/2次即可

• 时间复杂度：O(n^2)
• 稳定性：不稳定的算法
  代码实现：

void cocktail_sort(int arr[],size_t len)
{size_t i,j;for(i=0;i<len/2;i++){int max = i;	//最大值下标int min = i;	//最小值下标for(j=i+1;j<len-i;j++){if(arr[max]<arr[j]){	//找到最大值下标max = j;	}	if(arr[min]>arr[j]){	//找到最小值下标min = j;	}}if(max!=j-1){swap(&arr[max],&arr[j-1]);		//交换最大值和未进行排序的最后一个元素}if(min == j-1){	//如果最小值在未进行排序的最后一个位置，那么经过最大值的交换，已经交换到了最大值所在的位置min = max;		//把最小值的坐标进行改变}if(min!=i){swap(&arr[i],&arr[min]);	//交换最小值和未进行排序的最前的元素}}
}

7.堆排序

思路：把数据进行大堆化，然后依次交换堆顶(最大值)和最后一个元素,在使堆顶重新大堆化，最后循环过后数组便有序。
最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

• 时间复杂度：O(nlgn)
• 稳定性：不稳定的算法
  代码实现：

void re_heap(int arr[],size_t index,size_t len)
{size_t child = 2*index+1;	//左节点坐标int key = arr[index];	//当前节点值while(child<len){if(child+1<len&&arr[child]<arr[child+1]){	//如果右节点存在且右节点的值比左节点大，那就child记录较大字节点的坐标child++;	}	if(arr[child]>key){	//如果子节点的值比根节点的值大arr[index] = arr[child];	//改变根节点的值}else{break;	}index = child;child = 2*index+1;}arr[index] = key;		//插入记录好的值
}
void heap_sort(int arr[],size_t len)
{int i;for(i=len/2;i>=0;i--){re_heap(arr,i,len);		//对第i个根节点进行大堆化}for(i=len-1;i>0;i--){swap(&arr[0],&arr[i]);	//交换第一个和最后一个元素re_heap(arr,0,i);	//对第一个元素进行大堆化}
}

8.快速排序

思路：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
过程：

(1)首先设定一个分界值，通过该分界值将数组分成左右两部分

(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

• 时间复杂度：O(nlog2n)
• 稳定性：不稳定的算法
• 代码实现：

void quick_sort(int arr[],size_t left,size_t right)
{if(left>=right){	//如果只有一个元素，那就是有序的，返回return;	}int i = left;int j = right;int key = arr[left];	//基准值while(i<j){	//找到基准值的位置，使得基准值右边的元素都比基准值大，左边的元素都比基准值小while(i<j&&arr[j]>=key){	//从右边找一个比基准值小的数，--j;}arr[i] = arr[j];//把这个值放到基准值的位置处while(i<j&&arr[i]<=key){	//从左边找一个比基准值大的数++i;	}arr[j] = arr[i];		//把这个元素放到j的位置}arr[i] = key;if(i-left>1)	//元素个数至少两个才进行递归调用，这样可以少一次递归quick_sort(arr,left,i-1);	//对基准值左边的元素进行排序if(right-i>1)quick_sort(arr,i+1,right);	//对基准值右边的元素进行排序
}

9.归并排序

思路：对于两个有序的子序列，可以把它们合并在一起，变成一个新的完全有序的序列，因此归并排序和快排差不多，都是递归的进行。

• 时间复杂度：O(nlog2n)
• 稳定性：稳定的算法
  代码实现：

void merge(int arr[],int left,int right)
{int i,j,k;int mid = (left+right)/2;int len = mid-left+1;int *temp = malloc(sizeof(arr[0])*len);for(i=0;i<len;i++){temp[i] = arr[i+left];	//把这个数组的所有元素都复制到临时数组中}i=0,j=mid+1,k=left;while(i<len&&j<=right){if(temp[i]<arr[j]){	//把临时数组的元素和 [mid+1,right]这部分的元素一个一个的进行比较，如果谁小，那么arr里就存放谁的元素arr[k++] = temp[i++];	}else{arr[k++] = arr[j++];	}}while(i<len){	//如果temp这个数组的元素还没有全部遍历完，那就把temp后面的元素都复制到arr里面去，//因为arr[mid+1,right] 这部分的元素本来就是arr后面部分的有序的元素，所以如果arr[mid+1,right]这部分没有遍历完也没关系的，arr[k++] = temp[i++];	}free(temp);
}
void merge_sort(int arr[],int left,int right)
{if(left>=right){	//如果只有一个元素说明这个序列有序，那就返回return;	}	int mid = (left+right)/2;	//对两个有序的数组进行排序，merge_sort(arr,left,mid);	//对[left,mid]这个区间的元素进行排序merge_sort(arr,mid+1,right);	//对[mid+1,right]这个区间内的元素进行排序merge(arr,left,right);  //这个序列的[left,mid]为有序的序列 [mid+1,right]也为有序的序列
}

10.计数排序

思路：这是一种基于比较的算法，我们用一个大数组来存放这些数据，这些数据在这个大数组中的表现形式是以这个大数组的下标存在的，比如57,60,42这三个数字进行排序，那么用一个大数组，这个大数组的arr[57] = 1,arr[60] = 1,arr[42] = 1，然后遍历这个大数组就行了。

• 时间复杂度：O(n+k),其中这个k为数据的范围，所以计数排序最适合数据比较集中的数组排序。
• 稳定性：稳定的算法
• 代码实现：

void count_sort(int arr[],size_t len)
{int max = arr[0];	//最大值int min = arr[0];	//最小值size_t i;for(i=0;i<len;i++){if(max<arr[i]){	//找到最大值max =arr[i];	}if(min > arr[i]){	//找到最小值min = arr[i];	}}int cnt = max-min+1;		//范围int *prr = malloc(cnt*sizeof(int));	//申请临时空间for(i=0;i<cnt;i++){	//这个临时数组全部置0prr[i] = 0;	}for(i=0;i<len;i++){	//对需要进行排序的序列进行遍历prr[arr[i]-min]++;		//让下标为(arr[i]-min)的临时大数组的值+1}size_t j=0;for(i=0;i<cnt;i++){	//遍历这个临时数组while(prr[i]){	//如果这个数组下标为i的值不等于0arr[j++] = i+min;	//那就让需要进行排序的数组的值为i+min;--prr[i];}	}free(prr);		//释放掉申请的动态内存
}

11.桶排序

思路：工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。
这是一种以消耗大量空间来换取高效率的排序方式，

• 时间复杂度：O(N+C)，其中C=N*(logN-logM)，M为桶的数量。所以对于桶排序，桶的数量越多，其排序效率越高。
• 稳定性：稳定的算法

代码实现：
首先定义桶这个类型：

typedef struct Bucket
{int vect[100];	//其实这里使用链表更好，但是我比较懒，就懒得用链表了int cnt;	//当前桶内存放数据的个数
}Bucket;void bucket_sort(int arr[],size_t len)
{int min = arr[0];int max = arr[0];size_t i;for(i=0;i<len;i++){if(min>arr[i]){	//找到最小值min = arr[i];	}if(max<arr[i]){	//找到最大值max = arr[i];	}}int size = max-min+1;Bucket bucket[5] = {};	//其实桶可以动态规划，但为了方便我这里直接分为5个桶for(i=0;i<len;i++){	//遍历待排序的数组，把每个元素放到相应的桶当中，//比如[0,200]之间的元素放到下标为0的桶中，[201,400]之间的元素放到下标为1的桶中..//以此类推，直到放完所有的数据int index = (arr[i]-min)/(size/5);	//用来判断当前元素arr[i]需要放到哪个桶当中bucket[index].vect[bucket[index].cnt++] = arr[i];}size_t j=0,k=0;for(i=0;i<5;i++){	//对这五个桶进行遍历count_sort(bucket[i].vect,bucket[i].cnt);	//首先对这个桶内的元素进行排序，//这里可以调用其他排序方法，也可以递归调用当前排序方法，但是为了节省内存，我选择调用其他排序方法，for(j=0;j<bucket[i].cnt;j++){arr[k++] = bucket[i].vect[j];	//对排序好的桶进行遍历，并且把里面的元素复制到arr中去	}}
}

12.基数排序

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog®m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

解法：

1.首先根据个位数的数值，在走访数值时将它们分配至编号0到9的桶子中；

2.接下来将这些桶子中的数值重新串接起来，接着再进行一次分配，这次是根据十位数来分配；

3.接下来将这些桶子中的数值重新串接起来，持续进行以上的动作直至最高位数为止。

• 时间复杂度：设待排序列为n个记录，d个关键码，关键码的取值范围为radix，则进行链式基数排序的时间复杂度为O(d(n+radix))，其中，一趟分配时间复杂度为O(n)，一趟收集时间复杂度为O(radix)，共进行d趟分配和收集。
• 稳定性：稳定的算法；

代码实现：
还是定义桶的类型：

typedef struct Bucket{int vect[100];	//同样的可以用链表int cnt;
}Bucket;void base_sort(int arr[],size_t len)
{size_t i;Bucket bucket[10] = {};	//十个桶int max = arr[0];for(i=0;i<len;i++){	//寻找最大值，就可以判断最大值的位数if(arr[i]>max){max = arr[i];	}	}size_t j,k;int num = 1;	//用来获得相应位数上的数字的关键参数，//比如要获得个位上的参数时num = 1;//获得十位上的数字时num = 10;//以此类推do{for(i=0;i<len;i++){	//遍历待排序的数组，把每个元素放入相应的桶中//比如251，当获得个位上的数字时，251放到下标为1的桶当中//当获得十位上的数字时,251放到下标为5的桶当中//当获得百位上的数字时,251放到下标为2的桶当中//当获得千位上的数字时,251放到下标为0的桶当中//以此类推int index = arr[i]/num%10;	//获得相应位数上的数字bucket[index].vect[bucket[index].cnt++] = arr[i];	//把这个数字放到相应的桶中}k=0;for(i=0;i<10;i++){for(j=0;j<bucket[i].cnt;j++){arr[k++] = bucket[i].vect[j];	//把这些桶按顺序依次遍历，//把桶中的元素重新放回arr当中}	bucket[i].cnt = 0;	//记得让桶中的cnt变为0,方便下一次存放}num*=10;	//num*10}while(max/=10);//循环条件
}

=========以上内容来自：用C语言完整实现12种排序方法_c语言快速排序解决排序问题-CSDN博客============