Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数
题目
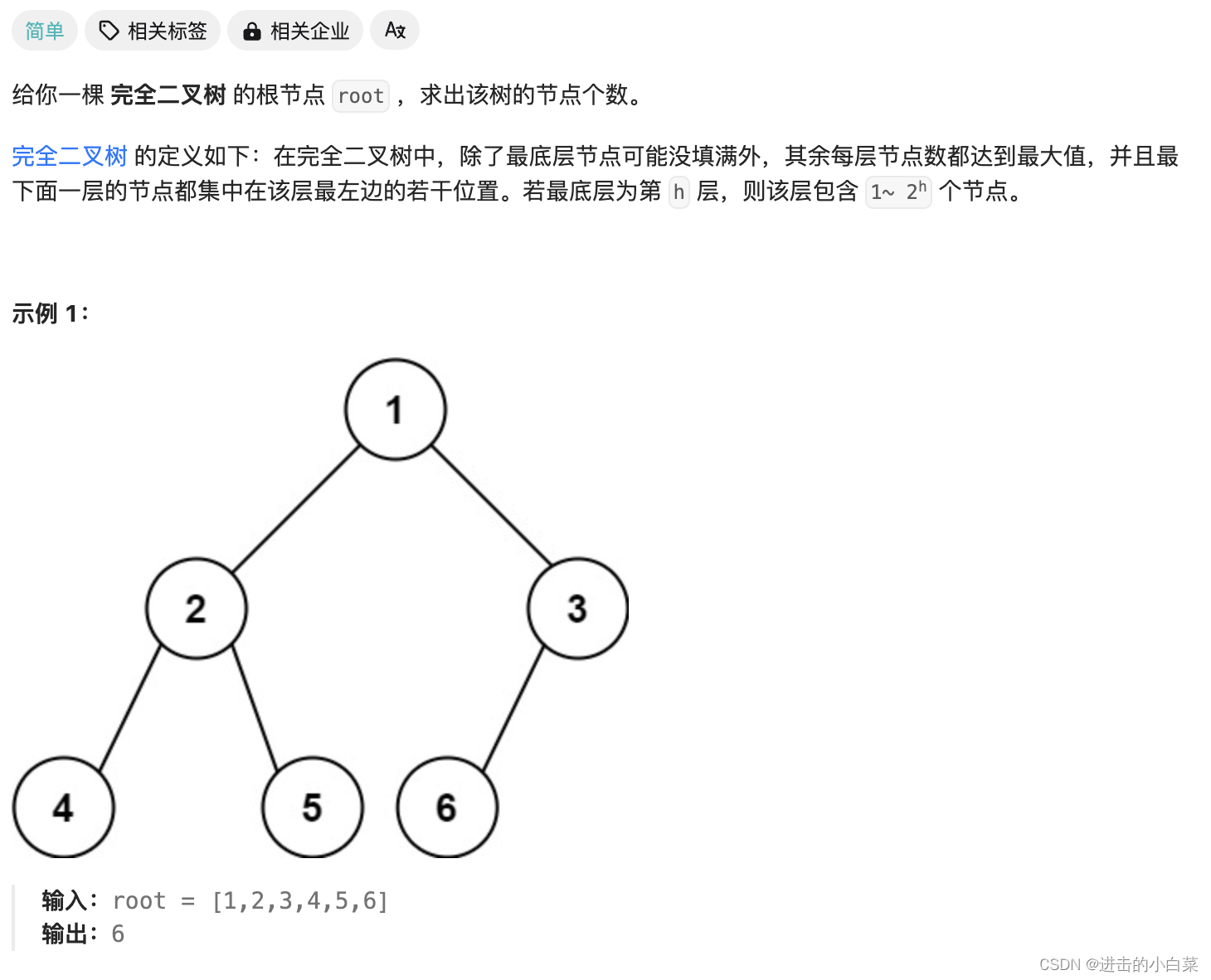
222.完全二叉树的节点个数
代码实现
class TreeNode {int val;TreeNode left, right;public TreeNode(int val) {this.val = val;this.left = this.right = null;}
}public class CompleteBinaryTreeCount {// 计算完全二叉树的节点个数public int countNodes(TreeNode root) {if (root == null) {return 0;}int leftHeight = leftHeight(root);int rightHeight = rightHeight(root);if (leftHeight == rightHeight) {// 左子树是满二叉树return (1 << leftHeight) - 1;} else {// 左子树不是满二叉树,递归计算左右子树的节点数return 1 + countNodes(root.left) + countNodes(root.right);}}// 计算左子树的高度private int leftHeight(TreeNode root) {int height = 0;while (root != null) {height++;root = root.left;}return height;}// 计算右子树的高度private int rightHeight(TreeNode root) {int height = 0;while (root != null) {height++;root = root.right;}return height;}public static void main(String[] args) {// 创建一个完全二叉树示例TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);root.right.left = new TreeNode(6);CompleteBinaryTreeCount solution = new CompleteBinaryTreeCount();int nodeCount = solution.countNodes(root);System.out.println("完全二叉树的节点个数: " + nodeCount);}
}
实现总结
- 完全二叉树:完全二叉树的定义是除了最后一层外,其它各层的节点数都达到最大值,且最后一层的节点依次从左到右排列。这一特性对计算节点数有重要影响。
- 确定解题方法:常见的方法包括递归和迭代。在了解完全二叉树的性质后,可以选择合适的方法求解节点数,上面实现就采用了递归的方式实现。
- 确定节点数计算方式:针对完全二叉树的特性,可以通过一些方法,如树的高度、子树的特性等来计算节点数。上面实现通过计算左子树和右子树的高度来确定完全二叉树的结构,如果左右子树高度相等,则左子树是满二叉树,节点个数可以通过2的幂次方计算。如果左右子树高度不等,则递归计算左右子树的节点数。
- 考虑边界情况:对于空树或者只有根节点的情况,需要特殊处理。
- 时间复杂度:
O(log^2 N)。递归的深度为树的高度,每次递归中需要计算左右子树的高度,因此时间复杂度为O(log N),其中 N 为节点个数。在每层递归中,都需要进行一次高度计算,高度计算的时间复杂度也为O(log N),因此总体时间复杂度为O(log^2 N)。