一、区间问题

①区间选点

算法
将所有区间的右端点从小到大排序
遍历所有的区间
若该区间内没有点（左端点大于标记值），则将该区间的右端点设为新的标记值，并且点数加一
若这个区间有点，则不处理，跳过该区间
代码

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;struct Range
{int l, r;bool operator<(const Range &w){return r < w.r;}
}range[N];int main()
{int n;cin >> n;for (int i = 0; i < n; i ++){int a, b;cin >> a >> b;range[i] = {a, b};}sort(range, range + n);int p = -2e9;int res = 0;for (int i = 0; i < n; i ++){if (range[i].l > p){res ++;p = range[i].r;}}cout << res;return 0;
}

②最大不相交区间数量

该题的算法与代码同上

③区间分组

算法
将所有区间按照左端点从小到大排序
遍历所有的区间
使用小根堆存储每个组最后一个区间的右端点值
如果当前区间的左端点 <= 堆中最小右端点
说明该区间不能放进任何一个分组，则将这个区间加入堆（新开一组）
如果当前区间左端点 > 堆中最小右端点
说明该区间能够放进任意一个组中，则将其放入右端点最小的组
将右端点最小的组的右端点更新
代码

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>using namespace std;const int N = 100010;struct Range
{int l, r;bool operator<(const Range &w){return l < w.l;}
}range[N];int main()
{int n;cin >> n;for (int i = 0; i < n; i ++){int a, b;cin >> a >> b;range[i] = {a, b};}sort(range, range + n);priority_queue <int, vector<int>, greater<int>> heap;int p = -2e9;for (int i= 0; i < n; i ++){if (heap.empty() || heap.top() >= range[i].l){heap.push(range[i].r);}else{heap.pop();heap.push(range[i].r);}}cout << heap.size();return 0;
}

④区间覆盖

算法
将所有区间按照左端点从小到大进行排序
遍历所有的区间
寻找覆盖st的所有区间中右端点最大的区间
并将该区间的右端点更新st，区间数量加一
若没有找到能够覆盖st的区间，则无解
若最后区间没有被覆盖完，则无解
代码

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;struct Range
{int l, r;bool operator<(const Range &w){return l < w.l;}
}range[N];int main()
{int st, ed;cin >> st >> ed;int n;cin >> n;for (int i = 0; i < n; i ++){int a, b;cin >> a >> b;range[i] = {a, b};}sort(range, range + n);bool f = false;int res = 0;for (int i = 0; i < n; i ++){int p = -2e9;int j = i;while (j < n && range[j].l <= st){p = max(p, range[j].r);j ++;}if (p < st){break;}if (p >= st){st = p;res ++;}if (p >= ed){f = true;break;}i = j - 1;}if (f) cout << res;else cout << -1;return 0;
}

二、Huffman树（合并果子）

算法
每次选取最小的两个数字进行合并
代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;const int N = 10010;int main()
{int n;cin >> n;priority_queue <int, vector <int>, greater<int>> heap;for (int i = 0; i < n; i ++){int x;cin >> x;heap.push(x);}int res = 0;while (heap.size() > 1){int a = heap.top();heap.pop();int b = heap.top();heap.pop();res += (a + b);heap.push(a + b);}cout << res;return 0;
}

三、排序不等式（排队打水）

算法
根据打水时间从小到大排队，即总的等待时间最短
代码

#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;
const int N = 100010;int a[N];
int main()
{int n;cin >> n;for(int i = 0; i < n; i ++) cin >> a[i];sort(a, a + n);long long res = 0;for (int i = 0; i < n; i ++) res += a[i] * (n - i - 1);cout << res;return 0;
}

四、绝对值不等式（货仓选址）

算法
如果有奇数个仓库，那么将地址选在中间那个仓库点就是距离最近的
如果有偶数个仓库，那么将地址选在中间两个仓库间的任何一点都是最近的
综上，选在n/2这个点即可涵盖上述两种情况
代码

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;
int a[N];
int n;int main()
{cin >> n;for (int i = 0; i < n; i ++) cin >> a[i];sort(a, a + n);int res = 0;for (int i = 0; i < n; i ++) res += abs(a[i] - a[n / 2]);cout << res;return 0;
}

五、推公式（耍杂技的牛）

算法
题目要考虑如何排序使得答案最小，可以尝试交换其中两头牛的位置
看看答案有什么影响，得出其中的公式，得到最优解

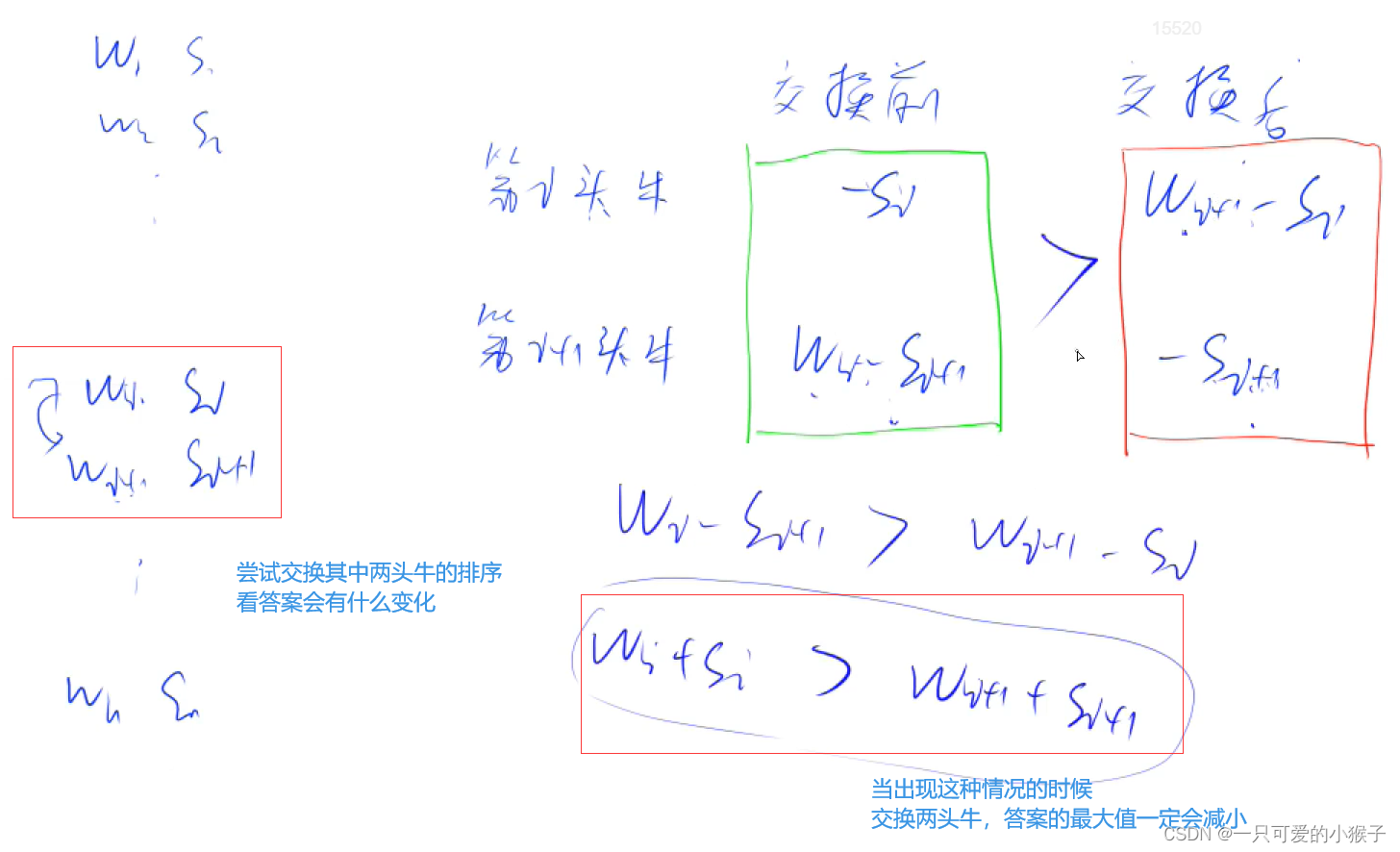
根据w + s 从小到大进行排序，得到的最大的风险系数最小
代码

#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;
typedef pair <int, int> PII;
const int N = 50010;PII a[N];int main()
{int n;cin >> n;for (int i = 0; i < n; i ++){int w, s;cin >> w >> s;a[i] = {w + s, s}; //第二个关键字是能力或体重都可以}sort(a, a + n);int res = -2e9, sum = 0;for (int i = 0; i < n; i ++){int s = a[i].second, w = a[i].first - s;res = max(res, sum - s);sum += w;}cout << res;return 0;
}