3.4 表面特性

        当光线穿过空间时，其中一些光线会与我们的物体相交。当这种情况发生时，光线会与物体表面相互作用，产生一种颜色。部分由此产生的颜色实际上并不是由直接光线产生的，而是来自其他物体反射或散射的环境光。环境光照模型对此进行了考虑，它是对现实世界中复杂光线散射的简单近似。它将光源的强度曲线应用于物体的颜色，也表示为强度曲线。结果就是我们在观察物体时所看到的光的颜色。在这样的模型中，重要的是要意识到，白色光照射到蓝色球上与蓝色光照射到白色球上是无法区分的。环境光照方程如下：

 

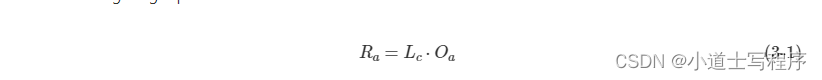
这段 大概是：

“ 在这里， Ra 是由环境光引起的最终强度曲线，Lc是环境光的强度曲线，而Oa是物体的颜色曲线。为了简化方程，我们假设所有方向向量都被标准化了（即，具有单位长度）。”

 

        得到的颜色的两个组成部分取决于直接光照。漫反射光照，也称为兰伯特反射，考虑了光线入射到物体上的角度。图3-7显示了一个圆柱体的图像，随着从中心向侧面移动，圆柱体变暗。圆柱体的颜色是恒定的；击中圆柱体表面的光的数量会发生变化。在中心，入射光几乎垂直于圆柱体表面，每个表面积收到更多的光线。当我们向侧面移动时，这个数量会减少，直到最终入射光线与圆柱体侧面平行，结果强度为零。

        图3-7. 平面和高拉德着色。不同的着色方法可以显著改善用多边形表示的物体的外观。顶部的平面着色使用每个多边形上的恒定表面法线。底部的高拉德着色插值多边形顶点的法线，使外观更加平滑。请参阅FlatVersusGouraud.cxx和FlatVersusGouraud.py。

        漫反射光照的贡献在方程3-2中表示，并在图3-8中进行了说明。

        镜面光照代表了光源在光滑物体上的直接反射。图3-10显示了一个漫反射光照的球体，具有不同的镜面反射。镜面强度（在顶部和底部行之间变化）控制了镜面光照的强度。镜面功率O_{sp}表示物体有多光滑，更具体地说，它表示了当反射角度偏离完美反射时镜面反射迅速减弱的速度。较高的值表示衰减更快，因此表面更光滑。参考图3-9，镜面光照的方程如下：

  这段原文大体：（请高手多指教）
“我们已经分别介绍了不同的光照模型的方程。我们可以同时或者结合应用所有的光照模型。方程3-4将环境光、漫反射光和镜面光结合成一个方程。

    结果是物体表面上的一个点的颜色。常数ka、kd和ks控制了物体环境光、漫反射光和镜面光的相对量。常数Ia、Id和Is指定了每种类型的光要使用的颜色。这六个常数以及镜面功率是表面材质属性的一部分。（其他属性，比如透明度，将在文本的后面部分介绍。）这些属性值的不同组合可以模拟出暗淡的塑料和抛光的金属。该方程假设了一个无限点光源，正如“光源”部分所描述的。然而，该方程可以很容易地修改以包含其他类型的定向光照。

”

图3-10. 镜面系数的效果。镜面系数控制物体的明亮度。顶部行具有镜面强度值为0.5；底部行为1.0。沿水平方向，镜面功率发生变化。数值（从左到右）分别为5、10、20和40。请参阅SpecularSpheres.cxx。

3.5 相机

        我们有发射光线的光源和具有表面属性的角色。在我们角色表面的每个点上，这种相互作用会产生一些复合颜色（即来自光线、物体表面、镜面和环境效果的组合颜色）。现在我们渲染场景所需要的就是相机。有一些重要因素决定了3D场景如何投影到平面上形成2D图像（见图3-11）。这些因素包括相机的位置、方向和焦点，相机投影方法以及相机裁剪平面的位置。

        图3-11 相机属性。

        相机的位置和焦点定义了相机的位置和指向位置。从相机位置到焦点定义的矢量被称为投影方向。相机图像平面位于焦点处，通常垂直于投影矢量。相机的方向由位置和焦点加上相机视角向量控制。这些完全定义了相机视图。

        投影方法控制了角色如何映射到图像平面。正交投影是一种平行映射过程。在正交投影（或平行投影）中，进入相机的所有光线都与投影矢量平行。透视投影发生在所有光线通过一个公共点（即视点或投影中心）的情况下。要应用透视投影，我们必须指定透视角度或相机视角。

        前后裁剪平面与投影矢量相交，通常垂直于它。裁剪平面用于消除距离相机太近或太远的数据。因此，只有在裁剪平面内的角色或角色部分是（可能）可见的。裁剪平面通常垂直于投影方向。它们的位置可以使用相机的裁剪范围来设置。平面的位置是从相机位置沿投影方向测量的。前裁剪平面位于最小范围值处，后裁剪平面位于最大范围值处。在第7章 - 高级计算机图形学中，当我们讨论立体渲染时，我们将看到不垂直于投影方向的裁剪平面的示例。

        综合起来，这些相机参数定义了一个矩形金字塔，其顶点位于相机的位置，沿投影方向延伸。金字塔在顶部被前裁剪平面截断，在底部被后裁剪平面截断。由此产生的视锥定义了相机可见的3D空间区域。

        虽然相机可以通过直接设置上述属性来进行操作，但也有一些常见的操作可以简化工作。图3-12和图3-13将帮助说明这些操作。改变相机的方位角会围绕其视角向量旋转其位置，以焦点为中心。可以将其视为将相机向左或向右移动，同时始终保持到焦点的距离不变。改变相机的仰角会围绕其投影方向和视角向量的叉积在焦点处旋转其位置。这相当于向上和向下移动相机。要旋转相机，我们围绕视平面法线旋转视角向量。旋转有时被称为扭转。

        接下来的两个动作保持相机的位置不变，而是修改焦点。改变偏航会围绕以相机位置为中心的视角向量旋转焦点。这类似于方位角，只是焦点移动而不是位置。俯仰的变化会围绕投影方向和视角向量的叉积在相机位置为中心旋转焦点。拉近和拉远会沿着投影方向移动相机的位置，靠近或远离焦点。此操作被指定为其当前距离与新距离的比值。大于一的值会拉近，小于一的值会拉远。最后，缩放会改变相机的视角，使场景的显示范围更多或更少。

 

图3-12. 环绕焦点的相机运动。请参阅CameraModel1.cxx和CameraModel1.py。

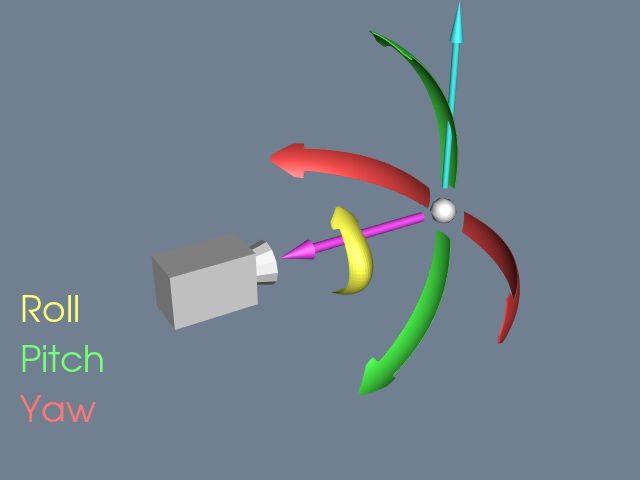
图3-13. 环绕相机位置的相机运动。请参阅CameraModel2.cxx和CameraModel2.py。

        一旦我们安置好相机，就可以生成我们的2D图像。穿过相机镜头的一些光线会穿过镜头。然后这些光线会击中一个平面，产生一幅图像。这实际上将我们的3D场景投影到2D图像中。相机的位置和其他属性决定了哪些光线被捕获和投影。更具体地说，只有与相机位置相交并在其视锥内的光线会影响最终的2D图像。

        这就结束了我们对渲染的简要概述。光线从光源传播到角色，被反射和散射。其中一些光线被相机捕获并产生一幅2D图像。现在我们将看一些这个过程的细节。

3.6 坐标系统

        计算机图形学中通常使用四种坐标系统以及表示其中点的两种不同方式（图3-14）。虽然这看起来有些多余，但每种坐标系统都有其特定用途。我们使用的四种坐标系统是：模型坐标系统、世界坐标系统、视图坐标系统和显示坐标系统。

        模型坐标系统是定义模型的坐标系统，通常是本地笛卡尔坐标系统。如果我们的一个角色代表一个足球，它将基于足球几何形状的自然坐标系统（例如，一个柱面坐标系统）。这个模型有一个固有的坐标系统，由生成它的人的决定确定。他们可能使用英寸或米作为单位，足球可能用任意轴作为其主轴进行建模。

        世界坐标系统是角色所处的3D空间。角色的一个职责是将模型的坐标转换为世界坐标。每个模型可能有自己的坐标系统，但只有一个世界坐标系统。每个角色必须将其模型缩放、旋转和平移到世界坐标系统中。（模型者可能还需要将其自然坐标系统转换为本地笛卡尔坐标系统。这是因为角色通常假定模型坐标系统是本地笛卡尔坐标系统。）世界坐标系统也是指定相机和光源位置和方向的系统。

        视图坐标系统表示相机可见的内容。它由一对x和y值组成，范围在(-1,1)之间，并且有一个z深度坐标。x、y值指定在图像平面中的位置，而z坐标表示距离或者说是相机的范围。相机的属性由一个四乘四的变换矩阵表示（稍后将描述），该矩阵用于将世界坐标转换为视图坐标。这是引入相机透视效果的地方。

        显示坐标系统与视图坐标系统使用相同的基础，但是不同于使用(-1,1)范围，它使用实际的x、y像素位置在图像平面上。诸如显示窗口大小的因素决定了(-1,1)视图坐标范围如何映射到像素位置。这也是视口产生作用的地方。

图3-14. 模型、世界、视图和显示坐标系统。

        您可能想渲染两个不同的场景，但在同一个窗口中显示它们。这可以通过将窗口分成矩形视口来实现。然后，可以告诉每个渲染器它应该使用窗口的哪个部分进行渲染。视口在x和y轴上的范围是(0,1)。与视图坐标系统类似，显示坐标系统中的z值也表示窗口的深度。这个z值的含义将在“Z缓冲区”部分进一步描述。