数据结构高级算法

 

目录

最小生成树

Kruskal(克鲁斯卡尔)(以边为核心)

9) 不相交集合（并查集合）

基础

Union By Size

图-相关题目

4.2 Greedy Algorithm

1) 贪心例子

Dijkstra

Prim

Kruskal

最优解（零钱兑换）- 穷举法 Leetcode 322

最优解（零钱兑换）- 贪心法 Leetcode 322

3) Huffman 编码问题

问题引入

Huffman 树

Huffman 编解码

4) 活动选择问题

无重叠区间-Leetcode 435

5) 分数背包问题

贪心法

6) 0-1 背包问题

贪心法

7) Set cover problem

4.3 Dynamic-Programming

1) Fibonacci

降维

2) 最短路径 - Bellman-Ford

3) 不同路径-Leetcode 62

降维

4) 0-1 背包问题

5) 完全背包问题

降维

6) 零钱兑换问题-Leetcode322

零钱兑换 II-Leetcode 518

7) 钢条切割问题

降维

类似题目 Leetcode-343 整数拆分

8) 最长公共子串

类似题目 Leetcode-718 最长重复子数组

两个字符串的删除操作-Leetcode 583

10) 最长上升子序列-Leetcode 300

11) Catalan 数

Leetcode-22 括号生成

买票找零问题

其它问题

12) 打家劫舍-Leetcode 198

13) Travelling salesman problem

其它题目

组合总和 IV-Leetcode 377

最小生成树

Prim
public class Prim {   public static void main(String[] args) {       Vertex v1 = new Vertex("v1");       Vertex v2 = new Vertex("v2");       Vertex v3 = new Vertex("v3");       Vertex v4 = new Vertex("v4");       Vertex v5 = new Vertex("v5");       Vertex v6 = new Vertex("v6");       Vertex v7 = new Vertex("v7");
​       v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 4), new Edge(v4, 1));       v2.edges = List.of(new Edge(v1, 2), new Edge(v4, 3), new Edge(v5, 10));       v3.edges = List.of(new Edge(v1, 4), new Edge(v4, 2), new Edge(v6, 5));       v4.edges = List.of(new Edge(v1, 1), new Edge(v2, 3), new Edge(v3, 2),               new Edge(v5, 7), new Edge(v6, 8), new Edge(v7, 4));       v5.edges = List.of(new Edge(v2, 10), new Edge(v4, 7), new Edge(v7, 6));       v6.edges = List.of(new Edge(v3, 5), new Edge(v4, 8), new Edge(v7, 1));       v7.edges = List.of(new Edge(v4, 4), new Edge(v5, 6), new Edge(v6, 1));
​       List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);
​       prim(graph, v1);
​   }
​   static void prim(List<Vertex> graph, Vertex source) {       ArrayList<Vertex> list = new ArrayList<>(graph);       source.dist = 0;
​       while (!list.isEmpty()) {//选取当前顶点           Vertex min = chooseMinDistVertex(list);
//更新当前顶点           updateNeighboursDist(min);
//移除当前顶点           list.remove(min);           min.visited = true;           System.out.println("---------------");           for (Vertex v : graph) {               System.out.println(v);           }       }
​
​   }
​   private static void updateNeighboursDist(Vertex curr) {       for (Edge edge : curr.edges) {           Vertex n = edge.linked;           if (!n.visited) {               int dist = edge.weight;               if (dist < n.dist) {                   n.dist = dist;                   n.prev = curr;               }           }       }   }
​   private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {       Vertex min = list.get(0);       for (int i = 1; i < list.size(); i++) {           if (list.get(i).dist < min.dist) {               min = list.get(i);           }       }       return min;   }
}
 

初始

 DIJKSTRA算法

Kruskal(克鲁斯卡尔)(以边为核心)

public class Kruskal {   static class Edge implements Comparable<Edge> {       List<Vertex> vertices;       int start;       int end;       int weight;
​       public Edge(List<Vertex> vertices, int start, int end, int weight) {           this.vertices = vertices;           this.start = start;           this.end = end;           this.weight = weight;       }
​       public Edge(int start, int end, int weight) {           this.start = start;           this.end = end;           this.weight = weight;       }
​       @Override       public int compareTo(Edge o) {           return Integer.compare(this.weight, o.weight);       }
​       @Override       public String toString() {           return vertices.get(start).name + "<->" + vertices.get(end).name + "(" + weight + ")";       }   }
​   public static void main(String[] args) {       Vertex v1 = new Vertex("v1");       Vertex v2 = new Vertex("v2");       Vertex v3 = new Vertex("v3");       Vertex v4 = new Vertex("v4");       Vertex v5 = new Vertex("v5");       Vertex v6 = new Vertex("v6");       Vertex v7 = new Vertex("v7");
​       List<Vertex> vertices = List.of(v1, v2, v3, v4, v5, v6, v7);       PriorityQueue<Edge> queue = new PriorityQueue<>(List.of(               new Edge(vertices,0, 1, 2),               new Edge(vertices,0, 2, 4),               new Edge(vertices,0, 3, 1),               new Edge(vertices,1, 3, 3),               new Edge(vertices,1, 4, 10),               new Edge(vertices,2, 3, 2),               new Edge(vertices,2, 5, 5),               new Edge(vertices,3, 4, 7),               new Edge(vertices,3, 5, 8),               new Edge(vertices,3, 6, 4),               new Edge(vertices,4, 6, 6),               new Edge(vertices,5, 6, 1)       ));
​       kruskal(vertices.size(), queue);   }
​   static void kruskal(int size, PriorityQueue<Edge> queue) {       List<Edge> result = new ArrayList<>();       DisjointSet set = new DisjointSet(size);       while (result.size() < size - 1) {           Edge poll = queue.poll();           int s = set.find(poll.start);           int e = set.find(poll.end);           if (s != e) {//未相交               result.add(poll);               set.union(s, e);//相交           }       }
​       for (Edge edge : result) {           System.out.println(edge);       }   }
}

9) 不相交集合（并查集合）

基础

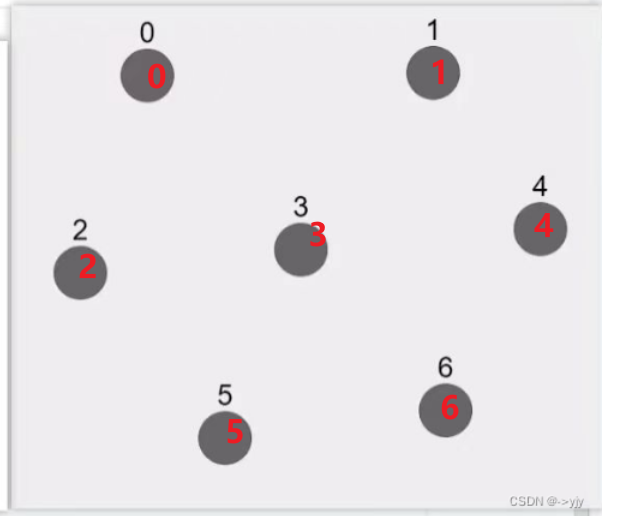
public class DisjointSet {   int[] s;   // 索引对应顶点   // 元素是用来表示与之有关系的顶点   /*       索引  0  1  2  3  4  5  6       元素 [0, 1, 2, 3, 4, 5, 6] 表示一开始顶点直接没有联系（只与自己有联系）
​   */
​   public DisjointSet(int size) {       s = new int[size];       for (int i = 0; i < size; i++) {           s[i] = i;       }   }
​   // find 是找到老大   public int find(int x) {       if (x == s[x]) {           return x;       }       return find(s[x]);   }
​   // union 是让两个集合“相交”，即选出新老大，x、y 是原老大索引   public void union(int x, int y) {       s[y] = x;   }
​   @Override   public String toString() {       return Arrays.toString(s);   }
​
}

路径压缩 直接改成老大

 public int find(int x) { // x = 2
    if (x == s[x]) {
        return x;
    }
    return s[x] = find(s[x]); // 0    s[2]=0
}

UnionBySize 

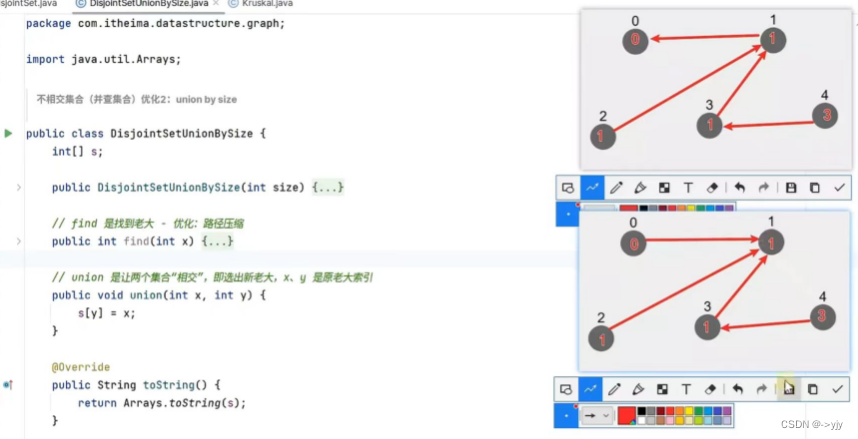
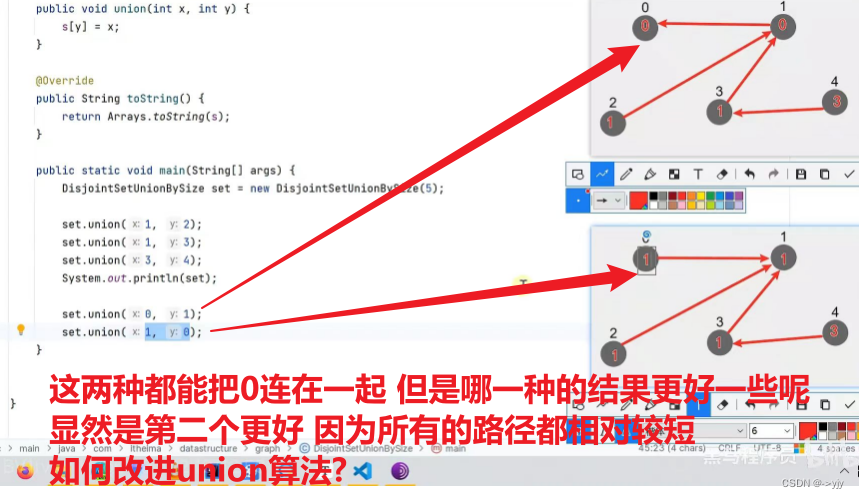
Union By Size
public class DisjointSetUnionBySize {   int[] s;   int[] size;//顶点个数多的当作老大比较合适 新的数组记录个数   public DisjointSetUnionBySize(int size) {       s = new int[size];       this.size = new int[size];       for (int i = 0; i < size; i++) {//初始化           s[i] = i;           this.size[i] = 1;       }   }
​   // find 是找到老大 - 优化：路径压缩   public int find(int x) { // x = 2       if (x == s[x]) {           return x;       }       return s[x] = find(s[x]); // 0    s[2]=0   }
​   // union 是让两个集合“相交”，即选出新老大，x、y 是原老大索引   public void union(int x, int y) {
//x 新老大 y新小弟
//        s[y] = x;       if (size[x] < size[y]) {
//y 老大 x小弟
//  s[x] = y;
//        size[y] = size[x] + size[y];//更新老大的元素个数           int t = x;           x = y;           y = t;       }       s[y] = x;       size[x] = size[x] + size[y];//更新老大的元素个数   }
​   @Override   public String toString() {       return "内容："+Arrays.toString(s) + "\n大小：" + Arrays.toString(size);   }
​   public static void main(String[] args) {       DisjointSetUnionBySize set = new DisjointSetUnionBySize(5);
​       set.union(1, 2);       set.union(3, 4);       set.union(1, 3);       System.out.println(set);   }
​
​
}

图-相关题目

题目编号题目标题算法思想
547省份数量DFS、BFS、并查集
797所有可能路径DFS、BFS
1584连接所有点的最小费用最小生成树
743网络延迟时间单源最短路径
787K 站中转内最便宜的航班单源最短路径
207课程表拓扑排序
210课程表 II拓扑排序

4.2 Greedy Algorithm

1) 贪心例子

称之为贪心算法或贪婪算法，核心思想是

  1. 将寻找最优解的问题分为若干个步骤

  2. 每一步骤都采用贪心原则，选取当前最优解(局部最优->全局最优)

  3. 因为没有考虑所有可能，局部最优的堆叠不一定让最终解最优

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择，从而希望导致结果是最好或最优的算法。这种算法通常用于求解优化问题，如最小生成树、背包问题等。

贪心算法的应用：

  1. 背包问题：给定一组物品和一个背包，每个物品有一定的重量和价值，要求在不超过背包容量的情况下，尽可能多地装入物品。

  2. 活动选择问题：在一个活动集合中，每次只能参加一个活动，问如何安排时间以最大化所有活动的收益。

  3. 编辑距离问题：给定两个字符串，求它们之间的最小编辑距离(即将一个字符串转换为另一个字符串所需的最少操作次数)。

  4. 网络流问题：给定一张有向图和一些起点和终点，求最大流量。

  5. 找零问题：给定一定数量的硬币和需要找零的金额，求使用最少的硬币数。

常见问题及解答：

  1. 贪心算法一定会找到最优解吗？ 答：不一定。贪心算法只保证在每一步选择中都是最优的，但并不能保证整个问题的最优解。例如，背包问题中的贪心算法可能会导致最后一个物品没有被装入背包。

  2. 如何判断一个问题是否适合用贪心算法解决？ 答：一个问题如果可以用递归的方式分解成若干个子问题，且每个子问题都有明确的最优解(即局部最优),那么这个问题就可以用贪心算法解决。

  3. 贪心算法的时间复杂度是多少？ 答：贪心算法的时间复杂度取决于问题的规模和具体实现。一般来说，对于规模较小的问题，贪心算法的时间复杂度可以达到O(nlogn)或O(n^2);对于规模较大的问题，可能需要O(n^3)或更高。

几个贪心的例子

Dijkstra
// ...
while (!list.isEmpty()) {   // 选取当前【距离最小】的顶点   Vertex curr = chooseMinDistVertex(list);   // 更新当前顶点邻居距离   updateNeighboursDist(curr);   // 移除当前顶点   list.remove(curr);   // 标记当前顶点已经处理过   curr.visited = true;
}

  • 没找到最短路径的例子：负边存在时，可能得不到正确解

  • 问题出在贪心的原则会认为本次已经找到了该顶点的最短路径，下次不会再处理它（curr.visited = true）

  • 与之对比，Bellman-Ford 并没有考虑局部距离最小的顶点，而是每次都处理所有边，所以不会出错，当然效率不如 Dijkstra

Prim
// ...
while (!list.isEmpty()) {   // 选取当前【距离最小】的顶点   Vertex curr = chooseMinDistVertex(list);   // 更新当前顶点邻居距离   updateNeighboursDist(curr);   // 移除当前顶点   list.remove(curr);   // 标记当前顶点已经处理过   curr.visited = true;
}
Kruskal
// ...
while (list.size() < size - 1) {   // 选取当前【距离最短】的边   Edge poll = queue.poll();   // 判断两个集合是否相交   int i = set.find(poll.start);   int j = set.find(poll.end);   if (i != j) { // 未相交       list.add(poll);       set.union(i, j); // 相交   }
}

其它贪心的例子

  • 选择排序、堆排序

  • 拓扑排序

  • 并查集合中的 union by size 和 union by height

  • 哈夫曼编码

  • 钱币找零，英文搜索关键字

    • change-making problem

    • find Minimum number of Coins

  • 任务编排

  • 求复杂问题的近似解

### 2) 零钱兑换问题#### 有几个解（零钱兑换 II）Leetcode 518```java
publi

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/252416.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

数字孪生网络攻防模拟与城市安全演练

数字孪生网络攻防模拟与城市安全演练

在数字化浪潮的推动下&#xff0c;网络攻防模拟和城市安全演练成为维护社会稳定的不可或缺的环节。基于数字孪生技术我们能够在虚拟环境中进行高度真实的网络攻防模拟&#xff0c;为安全专业人员提供实战经验&#xff0c;从而提升应对网络威胁的能力。同时&#xff0c;在城市安…
阅读更多...
day02-大盘板块功能实现

day02-大盘板块功能实现

day02-大盘板块功能实现 今日目标 完善基于前后端分离用户验证码登录功能;理解验证码生成流程,并使用postman测试;掌握SwaggerYapi使用理解并实现国内大盘数据展示功能;理解并实现国内板块数据展示功能;理解后端接口调试和前后端联调的概念; 第一章 验证码登录功能 1、前后…
阅读更多...
leetcode1079:游戏玩法分析——求留存率

leetcode1079:游戏玩法分析——求留存率

求留存率 题目描述题解 题目描述 表&#xff1a;Activity --------------------- | Column Name | Type | --------------------- | player_id | int | | device_id | int | | event_date | date | | games_played | int | --------------------- &#xff08;player_id&…
阅读更多...
第5课 使用FFmpeg将rtmp流再转推到rtmp服务器

第5课 使用FFmpeg将rtmp流再转推到rtmp服务器

本课对应源文件下载链接&#xff1a; https://download.csdn.net/download/XiBuQiuChong/88801992 通过前面的学习&#xff0c;我们已经可以正常播放网络rtmp流及本地mp4文件。这节课&#xff0c;我们将在前面的基础上实现一个常用的转推功能&#xff1a;读取rtmp流或mp4文件并…
阅读更多...
嵌入式软件的设计模式与方法

嵌入式软件的设计模式与方法

思想有多远&#xff0c;我们就能走多远 4、状态与工作流类设计模式 4.1 状态与事件 行为随条件变化而改变&#xff0c;这里状态切换的模式也称为状态机。有限状态机 (Finite State Machine&#xff0c;FSM) 是由3 个主要元素组成的有向图: 状态、转换和动作。 状态是系统或者…
阅读更多...
jmeter-04创建请求

jmeter-04创建请求

文章目录 一、发送请求-查看响应流程二、新建请求三、选择请求方式&#xff0c;填写url1.发送get请求当只有请求方式不一样的时候&#xff0c;参数都填写在参数栏里面&#xff0c;GET请求与POST请求的区别&#xff1f; 2.发送post请求2.1 application/x-www-form-urlencoded2.2…
阅读更多...
vue element 组件 form深层 :prop 验证失效问题解决

vue element 组件 form深层 :prop 验证失效问题解决

此图源自官网 借鉴。 当我们简单单层验证的时候发现是没有问题的&#xff0c;但是有的时候可能会涉及到深层prop&#xff0c;发现在去绑定的时候就不生效了。例如我们在form单里面循环验证&#xff0c;在去循环数据验证。 就如下图的写法了 :prop"pumplist. i .device…
阅读更多...
AI数字人训练数据集汇总

AI数字人训练数据集汇总

唇读&#xff08;Lip Reading&#xff09;&#xff0c;也称视觉语音识别&#xff08;Visual Speech Recognition&#xff09;&#xff0c;通过说话者口 型变化信息推断其所说的内容&#xff0c;旨在利用视觉信道信息补充听觉信道信息&#xff0c;在现实生活中有重要应用。例如&…
阅读更多...
WINDOWS搭建NFS服务器

WINDOWS搭建NFS服务器

下载并安装 Networking Software for Windows 启动配置 找到安装目录&#xff08;如C:\Program Files\nfsd&#xff09;&#xff0c;双击nfsctl.exe&#xff0c;菜单Edit->Preferences 启动后&#xff1a; 配置Export Exports->Edit exports file 其他的几句我都删除…
阅读更多...
Maven的安装以及配置（超级详细版）

Maven的安装以及配置（超级详细版）

前言 至于什么是Maven&#xff0c;大家可以理解为之前的Vue一样&#xff0c;也是通过操控对象映射来使用的 他内部还有很多的插件用于实现对应的功能&#xff0c;例如打包插件&#xff0c;或是测试 maven下载 Maven – Download Apache Maven apache下的开源项目&#xff0c…
阅读更多...
【Docker】.NET Core 6.0 webapi 发布上传到Docker Desktop并启动运行访问，接口返回数据乱码解决方法

【Docker】.NET Core 6.0 webapi 发布上传到Docker Desktop并启动运行访问，接口返回数据乱码解决方法

欢迎来到《小5讲堂》&#xff0c;大家好&#xff0c;我是全栈小5。 这是《Docker容器》系列文章&#xff0c;每篇文章将以博主理解的角度展开讲解&#xff0c; 特别是针对知识点的概念进行叙说&#xff0c;大部分文章将会对这些概念进行实际例子验证&#xff0c;以此达到加深对…
阅读更多...
车载测试中：如何处理 bug

车载测试中：如何处理 bug

一&#xff1a;Jira 提交 bug 包含那些内容 二&#xff1a;如何处理现上 bug 三&#xff1a;车载相关的 bug 如何定位 四&#xff1a;遇到 bug &#xff0c;复现不出来怎么办 五&#xff1a;bug 的处理流程 一&#xff1a;Jira 提交 bug 包含那些内容二&#xff1a;如何处理现上…
阅读更多...
ReactNative实现一个圆环进度条

ReactNative实现一个圆环进度条

我们直接看效果&#xff0c;如下图 我们在直接上代码 /*** 圆形进度条*/ import React, {useState, useEffect} from react; import Svg, {Circle,G,LinearGradient,Stop,Defs,Text, } from react-native-svg; import {View, StyleSheet} from react-native;// 渐变色 const C…
阅读更多...
点云transformer算法: FlatFormer 论文阅读笔记

点云transformer算法: FlatFormer 论文阅读笔记

代码&#xff1a;https://github.com/mit-han-lab/flatformer论文&#xff1a;https://arxiv.org/abs/2301.08739[FlatFormer.pdf] Flatformer是对点云检测中的 backbone3d部分的改进工作&#xff0c;主要在探究怎么高效的对点云应用transformer 具体的工作如下&#xff1a;一…
阅读更多...
可解释性AI（XAI）的主要实现方法和研究方向

可解释性AI（XAI）的主要实现方法和研究方向

文章目录 每日一句正能量前言主要实现方法可解释模型模型可解释技术 未来研究方向后记 每日一句正能量 当你还不能对自己说今天学到了什么东西时&#xff0c;你就不要去睡觉。 前言 随着人工智能的迅速发展&#xff0c;越来越多的决策和任务交给了AI系统来完成。然而&#xff…
阅读更多...
JAVA代理模式详解

JAVA代理模式详解

代理模式 1 代理模式介绍 在软件开发中,由于一些原因,客户端不想或不能直接访问一个对象,此时可以通过一个称为"代理"的第三者来实现间接访问.该方案对应的设计模式被称为代理模式. 代理模式(Proxy Design Pattern ) 原始定义是&#xff1a;让你能够提供对象的替代…
阅读更多...
python统计文本 2022年9月青少年电子学会等级考试 中小学生python编程等级考试二级真题答案解析

python统计文本 2022年9月青少年电子学会等级考试 中小学生python编程等级考试二级真题答案解析

目录 python统计文本 一、题目要求 1、编程实现 2、输入输出
阅读更多...
【多模态MLLMs+图像编辑】MGIE：苹果开源基于指令和大语言模型的图片编辑神器（24.02.03开源）

【多模态MLLMs+图像编辑】MGIE：苹果开源基于指令和大语言模型的图片编辑神器（24.02.03开源）

项目主页&#xff1a;https://mllm-ie.github.io/ 论文 :基于指令和多模态大语言模型图片编辑 2309.Guiding Instruction-based Image Editing via Multimodal Large Language Models &#xff08;加州大学圣巴拉分校苹果&#xff09; 代码&#xff1a;https://github.com/appl…
阅读更多...
MySQL 时间索引的选择

MySQL 时间索引的选择

背景 MySQL 在使用过程中经常会对时间加索引&#xff0c;方便进行时间范围的查询&#xff0c;常见的时间类型有 data、datetime、long、timestamp 等&#xff0c;在此分析下这几种时间类型的索引大小&#xff0c;以找到比较合适的时间类型。 时间类型对比 常用的索引类型是 …
阅读更多...
YIA主题如何关闭新版本升级提示？WordPress主题怎么取消升级提醒？

YIA主题如何关闭新版本升级提示？WordPress主题怎么取消升级提醒？

前两天YIA主题发布了升级到2.8版本&#xff0c;新增了一些功能&#xff0c;优化调整修复了一些功能&#xff0c;但是这些功能调整幅度不大&#xff0c;加上boke112百科使用的YIA主题已经进行了很多方面的个性化修改&#xff0c;所以就懒得升级了&#xff0c;但是每次进入WordPr…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023