【C语言】位与移位操作符详解

1.⼆进制和进制转换

①十进制：生活中最常用

②二进制：计算机中使用的，每个数字称为一个比特

③八进制、十六进制也如上

④二进制转十进制

⑤十进制转二进制

⑥二进制转八进制

⑦二进制转十六进制

2.原码、反码、补码

3.移位操作符（对于数值的二进制操作）

①左移操作符<<

②右移操作符>>

4.位操作符：&、|、^、~

①按位与&

②按位或|

③按位异或^

④按位取反~

5.结语

对于C语言中位操作符的介绍首先我们要先了解一些预备知识

1.⼆进制和进制转换

其实2进制、8进制、10进制、16进制是数值的不同表⽰形式⽽已。

例如：

数值15的各种进制的表⽰形式：

二进制	1111
八进制	17
十进制	15
十六进制	F

①十进制：生活中最常用

（1）逢十进一

（2）数字每一位由0~9中的数字组成

②二进制：计算机中使用的，每个数字称为一个比特

（1）逢二进一

（2）数字每一位由0~1中的数字组成

③八进制、十六进制也如上

④二进制转十进制

其实各种进制的每一位都是有相对应的权重的，例如十进制中123为什么是这个值呢？

10进制的位	1	2	3
权重	$10^{2}$	$10^{1}$	$10^{0}$
求值	1 * 100 + 2 * 10 +3 * 1 = 123

我们可以看到十进制从右往左个、十、百...位权重依次是 $10^{0}$ 、 $10^{1}$ 、 $10^{2}$ ...

2进制和10进制是类似的，只不过2进制的每⼀位的权重，从右向左是: $2^{0}$ 、 $2^{1}$ 、 $2^{2}$ ...

例如：

二进制的位	1	1	0
权重	$2^{2}$	$2^{1}$	$2^{0}$
求值	1 * 4 + 1 * 2 + 0 * 1 = 6

⑤十进制转二进制

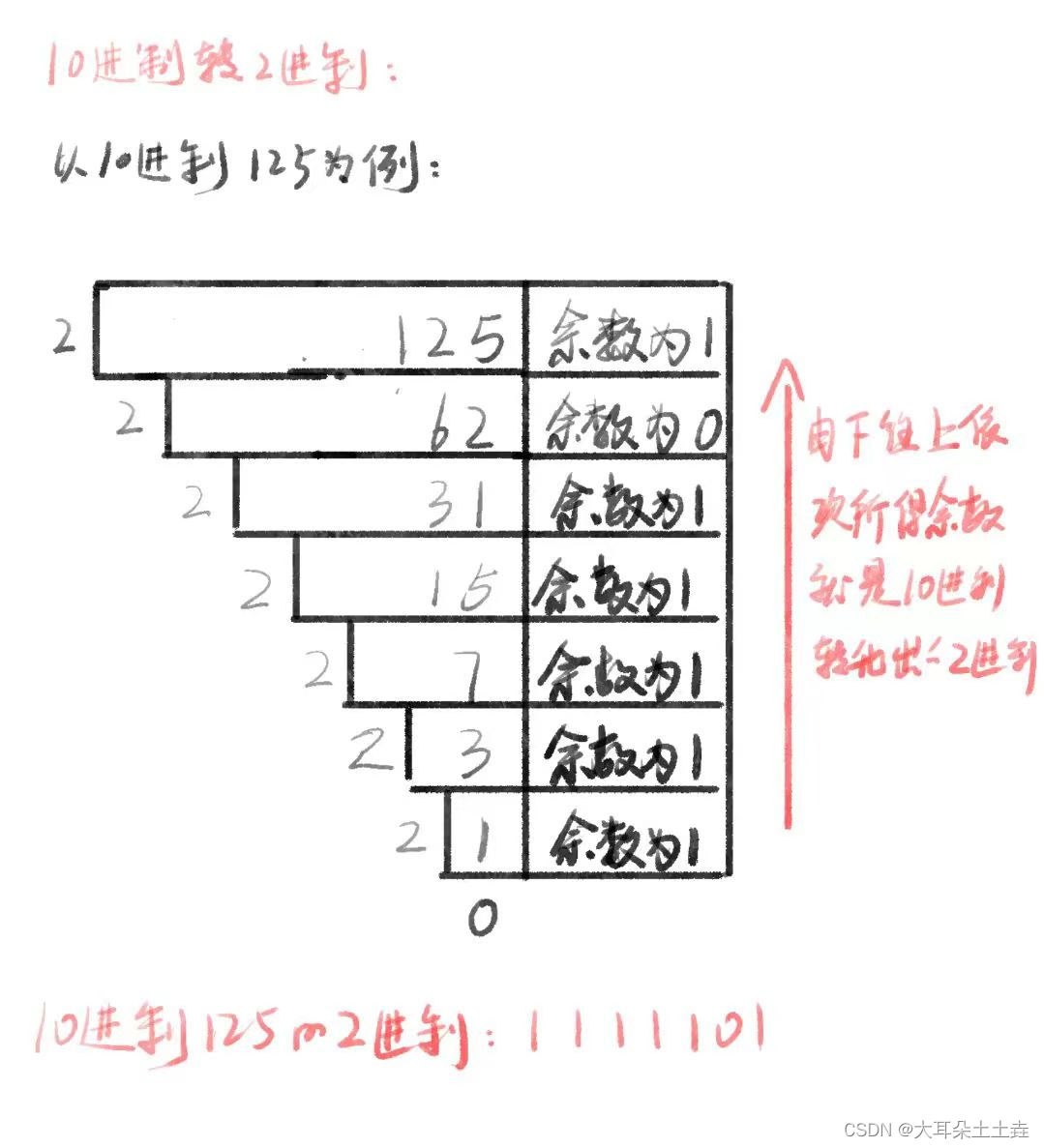
⑥二进制转八进制

8进制的数字每⼀位是 0~7 的，0~7的数字，各⾃写成2进制，最多有 3个2进制位就⾜够了，比如7的二进制是111，所以在2进制转8进制数的时候，从2进制序列中右边低位开始向左每3个2进制位会换算一个8进制位，剩余不够3个2进制位的直接换算。

例如：

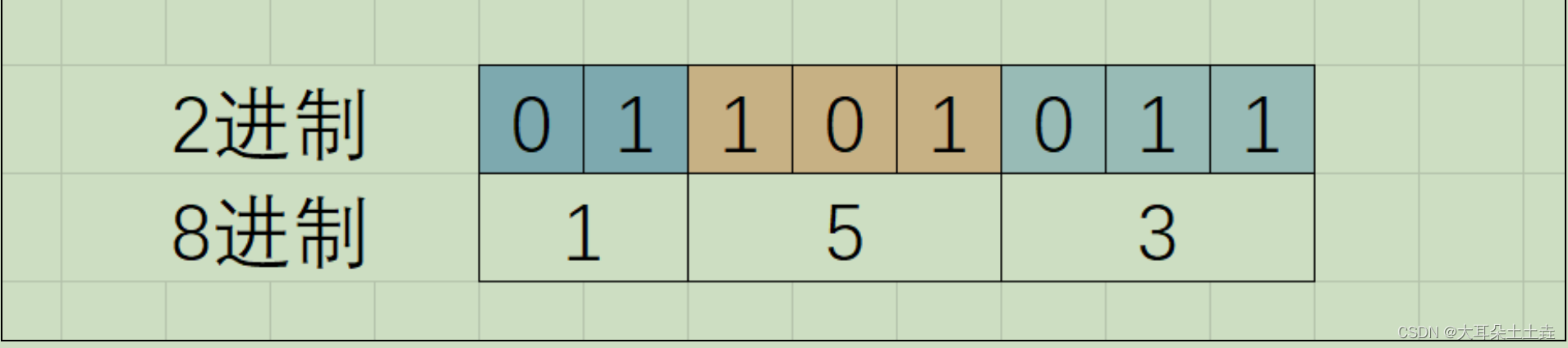
⑦二进制转十六进制

16进制的数字每⼀位是 0~9,a ~f 的，0~9,a ~f的数字，各⾃写成2进制，最多有4个2进制位就⾜够了，⽐如 f 的⼆进制是1111，所以在2进制转16进制数的时候，从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位，剩余不够4个⼆进制位的直接换算。

如：2进制的01101011，换成16进制： 0x6b ，16进制表示的时候前⾯加0x

2.原码、反码、补码

①整数的二进制表示方法有三种：原码、反码、补码

②有符号整数三种表示方式均有符号位与数值位两部分，在二进制序列中最高的一位是符号位，其余的是数值位；

③符号位的0表示“ 正”，1表示“ 负”；

原码：直接将数据翻译成二进制的形式就可以

例：10 翻译成二进制就是 1010 再根据数据开辟的内存空间补充0或1就可（正数符号位即第一位补0负数符号位补1，其余都补0）

int 10就是开辟了4个字节有32个比特位即00000000 00000000 00000000 00001010为二进制表示

int -10的二进制原码即为10000000 00000000 00000000 00001010

反码：将原码的符号位不变其余按位取反

例：int -10反码：11111111 111111111 11111111 11110101

补码：反码+1即可

例：int -10补码：11111111 11111111 11111111 11110110

注意：1.正数的原码、反码、补码相同

2.对于整型来说：数据在内存中存放的是补码

存放补码的原因在于:

在计算机系统中，数值⼀律⽤补码来表⽰和存储。原因在于，使⽤补码，可以将符号位和数值域统处理；同时，加法和减法也可以统⼀处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路.

3.移位操作符（对于数值的二进制操作）

<< 左移操作符

>> 右移操作符

注：移位操作符的操作数只能是整数。

①左移操作符<<

规则：左边抛弃，右边补零

②右移操作符>>

规则：

⾸先右移运算分两种：

1. 逻辑右移：左边⽤0填充，右边丢弃

2. 算术右移：左边⽤原该值的符号位填充，右边丢弃

注：对于移位运算符，不要移动负数位，这个是标准未定义的。

例如：

int num = 10;
num>>-1;//error

4.位操作符：&、|、^、~

&        //按位与    将两操作数二进制每一位对比同时为1时结果为1，否则为0
|        //按位或    同时为0时为0，其余为1
^        //按位异或  相同为0，否则为1
~        //按位取反  同反码的运算

注：它们的操作数必须是整数，负数用二进制的补码进行运算

例如：

#include <stdio.h>
int main()
{int num1 = -3;int num2 = 5;printf("按位与&：%d\n", num1 & num2);printf("按位或|：%d\n", num1 | num2);printf("按位异或^：%d\n", num1 ^ num2);printf("按位取反~：%d\n", ~0);return 0;
}

结果如下：

①按位与&

-3取其补码

按位与同数学中的逻辑运算与，同真才为真（两个都是1才为1），其余为假（0）；

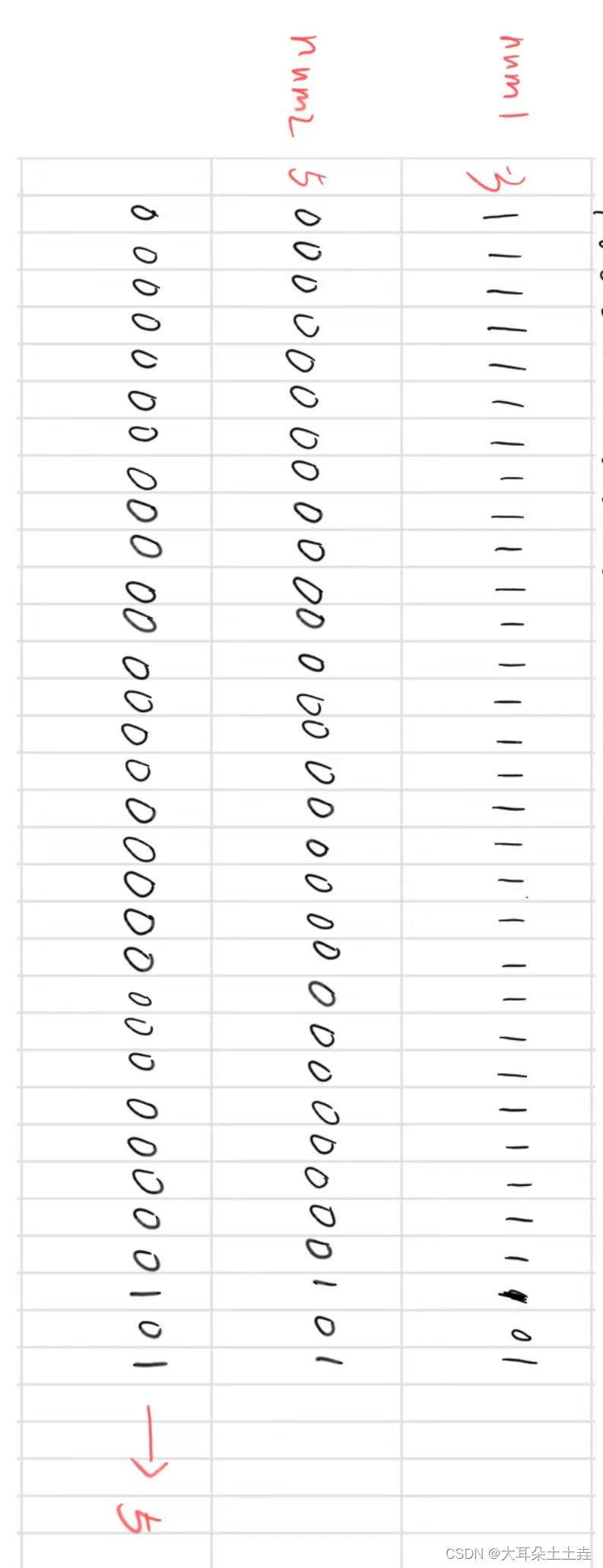
②按位或|

按位或类似于数学中逻辑与算符或：

只要有一个真则为真其余为假（只要有一个1则为1，其余为0）

③按位异或^

相异为真（01则为1，其余为0）

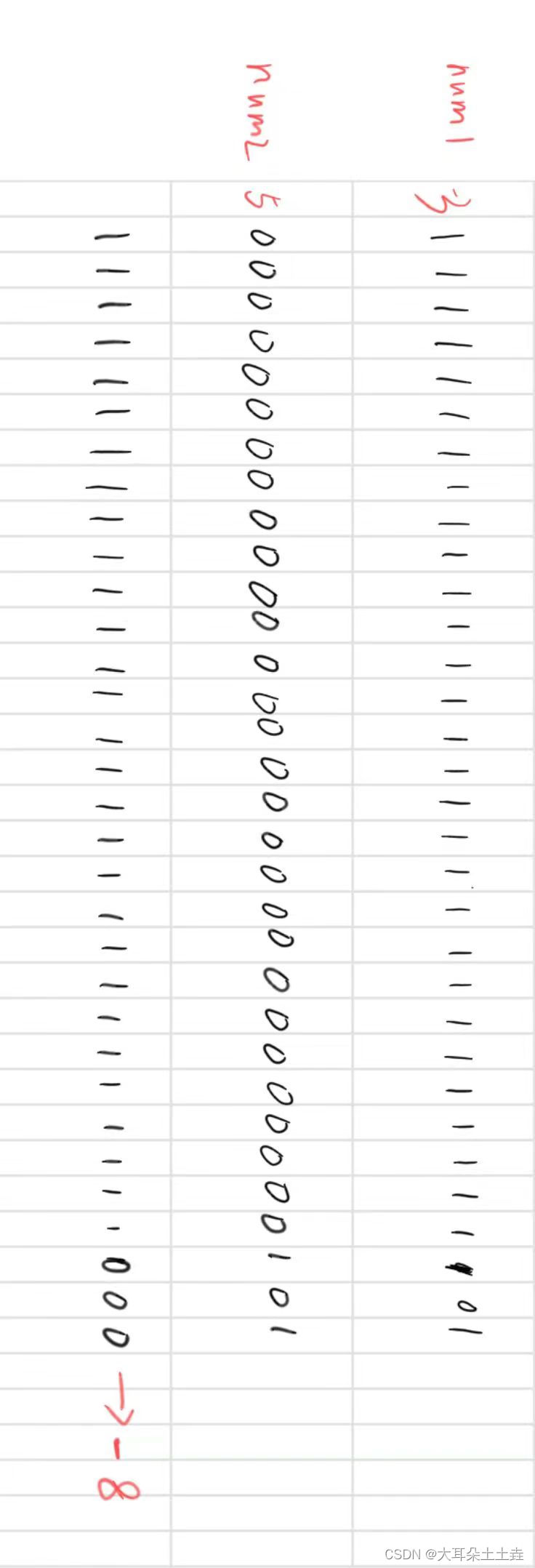
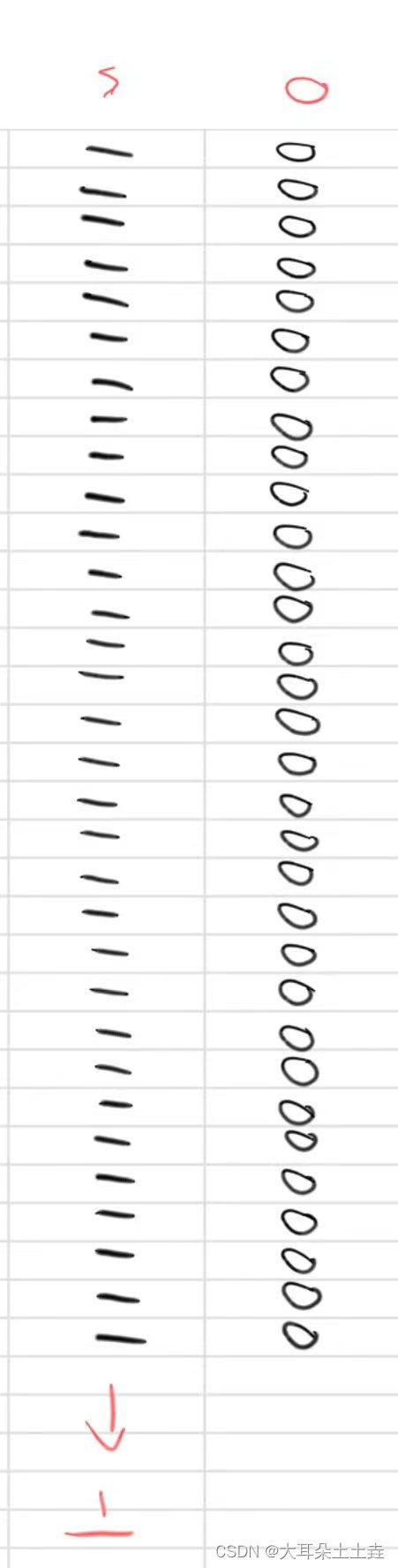
④按位取反~

取相反值就行

5.结语

位与移位操作符是c语言学习中的一个难点，其关键在于对于二进制的了解与使用，熟悉各种操作符的使用规则，以上就是今天学习的内容啦~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/253456.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！