原题链接:3027. 人员站位的方案数 II
题目描述:
给你一个 n x 2 的二维数组 points ,它表示二维平面上的一些点坐标,其中 points[i] = [xi, yi] 。
我们定义 x 轴的正方向为 右 (x 轴递增的方向),x 轴的负方向为 左 (x 轴递减的方向)。类似的,我们定义 y 轴的正方向为 上 (y 轴递增的方向),y 轴的负方向为 下 (y 轴递减的方向)。
你需要安排这 n 个人的站位,这 n 个人中包括 liupengsay 和小羊肖恩 。你需要确保每个点处 恰好 有 一个 人。同时,liupengsay 想跟小羊肖恩单独玩耍,所以 liupengsay 会以 liupengsay 的坐标为 左上角 ,小羊肖恩的坐标为 右下角 建立一个矩形的围栏(注意,围栏可能 不 包含任何区域,也就是说围栏可能是一条线段)。如果围栏的 内部 或者 边缘 上有任何其他人,liupengsay 都会难过。
请你在确保 liupengsay 不会 难过的前提下,返回 liupengsay 和小羊肖恩可以选择的 点对 数目。
注意,liupengsay 建立的围栏必须确保 liupengsay 的位置是矩形的左上角,小羊肖恩的位置是矩形的右下角。比方说,以 (1, 1) ,(1, 3) ,(3, 1) 和 (3, 3) 为矩形的四个角,给定下图的两个输入,liupengsay 都不能建立围栏,原因如下:
- 图一中,liupengsay 在
(3, 3)且小羊肖恩在(1, 1),liupengsay 的位置不是左上角且小羊肖恩的位置不是右下角。 - 图二中,liupengsay 在
(1, 3)且小羊肖恩在(1, 1),小羊肖恩的位置不是在围栏的右下角。

输入输出描述:
示例 1:
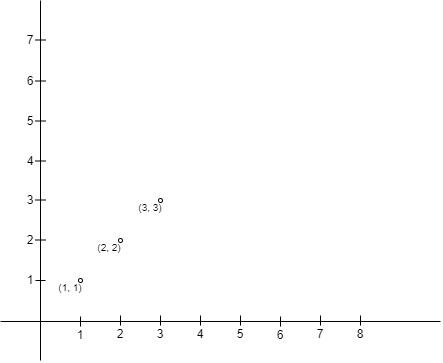
输入:points = [[1,1],[2,2],[3,3]] 输出:0 解释:没有办法可以让 liupengsay 的围栏以 liupengsay 的位置为左上角且小羊肖恩的位置为右下角。所以我们返回 0 。
示例 2:
编辑
输入:points = [[6,2],[4,4],[2,6]] 输出:2 解释:总共有 2 种方案安排 liupengsay 和小羊肖恩的位置,使得 liupengsay 不会难过: - liupengsay 站在 (4, 4) ,小羊肖恩站在 (6, 2) 。 - liupengsay 站在 (2, 6) ,小羊肖恩站在 (4, 4) 。 不能安排 liupengsay 站在 (2, 6) 且小羊肖恩站在 (6, 2) ,因为站在 (4, 4) 的人处于围栏内。
示例 3:
编辑
输入:points = [[3,1],[1,3],[1,1]] 输出:2 解释:总共有 2 种方案安排 liupengsay 和小羊肖恩的位置,使得 liupengsay 不会难过: - liupengsay 站在 (1, 1) ,小羊肖恩站在 (3, 1) 。 - liupengsay 站在 (1, 3) ,小羊肖恩站在 (1, 1) 。 不能安排 liupengsay 站在 (1, 3) 且小羊肖恩站在 (3, 1) ,因为站在 (1, 1) 的人处于围栏内。 注意围栏是可以不包含任何面积的,上图中第一和第二个围栏都是合法的。
提示:
2 <= n <= 1000points[i].length == 2-10^9 <= points[i][0], points[i][1] <= 10^9points[i]点对两两不同。
解题思路:
方法1:离散化前缀和
这个题目看一眼就知道是二维前缀和,只不过值域非常大,需要离散化,我们可以将x,y坐标放在一起离散化,也可以分开离散化,分开离散化时间和空间要求都低一些,所以我们分开离散化即可,由于需要使用前缀和,所以离散x的同时肯定还要离散化x-1,离散化y的同时还要离散化y-1。
时间复杂度:O(n^2),但是n最大2000。
空间复杂度:O(n^2),n最大2000。
按道理这个时间复杂度是能过的,但是由于这个双周赛case设计有问题,数据非常弱,导致比赛时很多O(n^3)暴力都水过去了,然后赛后为了卡掉那些暴力,加了一些case,可能还把时间限制放的很低,导致这个写法有时候能过,有时候会超时,相当于这个做法也被卡常了,我已经试过了,交了几发,有时候能过,有时候过不了。
离散化前缀和cpp代码如下:
const int N=2010;
int s[N][N];
class Solution {
public:int numberOfPairs(vector<vector<int>>& points) {unordered_map<int,int>mp1,mp2; //mp1用于离散化x坐标,mp2离散化y坐标vector<int>nums1,nums2;int n=points.size();int cnt1=0,cnt2=0;for(auto& t:points){int x=t[0],y=t[1];nums1.push_back(x);nums1.push_back(x-1);nums2.push_back(y);nums2.push_back(y-1);}//x,y坐标分别离散化sort(nums1.begin(),nums1.end());sort(nums2.begin(),nums2.end());for(int i=0;i<nums1.size();i++){int v1=nums1[i],v2=nums2[i];if(i==0)mp1[v1]=++cnt1,mp2[v2]=++cnt2;else {if(nums1[i]!=nums1[i-1])mp1[nums1[i]]=++cnt1;if(nums2[i]!=nums2[i-1])mp2[nums2[i]]=++cnt2;}}//根据离散化之后x,y坐标数,初始化前缀和int mx1=cnt1,mx2=cnt2;// vector<vector<int>>s(mx1+1,vector<int>(mx2+1));for(int i=1;i<=mx1;i++)for(int j=1;j<=mx2;j++)s[i][j]=0;for(auto&t:points){int x=t[0],y=t[1];s[mp1[x]][mp2[y]]++;}//预处理前缀和for(int i=1;i<=mx1;i++)for(int j=1;j<=mx2;j++)s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];//枚举int ans=0;for(int i=0;i<n;i++){int x1=mp1[points[i][0]],y1=mp2[points[i][1]];for(int j=0;j<n;j++){if(i==j)continue;int x2=mp1[points[j][0]],y2=mp2[points[j][1]];if(x2>=x1 && y2<=y1){if(s[x2][y1]-s[x2][y2-1]-s[x1-1][y1]+s[x1-1][y2-1]==2){ans++;}}}}return ans;}
};方法二:挖掘性质+枚举
首先题目说了一个在左上角,一个在右下角,从左往右横坐标x递增,从上往下纵坐标递减,所以我们从按照横坐标从小到达排序,横坐标相同时,纵坐标从大到小排序,固定i,从j=i+1枚举,那么j的纵坐标必须小于等于i的纵坐标,同时j的纵坐标必须大于前面枚举的所有点的纵坐标,才能保证i为左上角,j为右下角的矩形里面和边界没有其他点。
时间复杂度:O(n^2)
空间复杂度:O(1),不考虑排序使用的栈空间。
挖掘性质+枚举cpp代码如下:
class Solution {
public:int numberOfPairs(vector<vector<int>>& points) {sort(points.begin(),points.end(),[&](vector<int>&A,vector<int>&B){return A[0]!=B[0]?A[0]<B[0]:A[1]>B[1];});int ans=0,n=points.size();for(int i=0;i<n;i++){int y1=points[i][1];int max_y=-1e9-1;for(int j=i+1;j<n;j++){int y=points[j][1];if(y<=y1 && y>max_y){ans++;max_y=y;}}}return ans;}
};