题面

链接

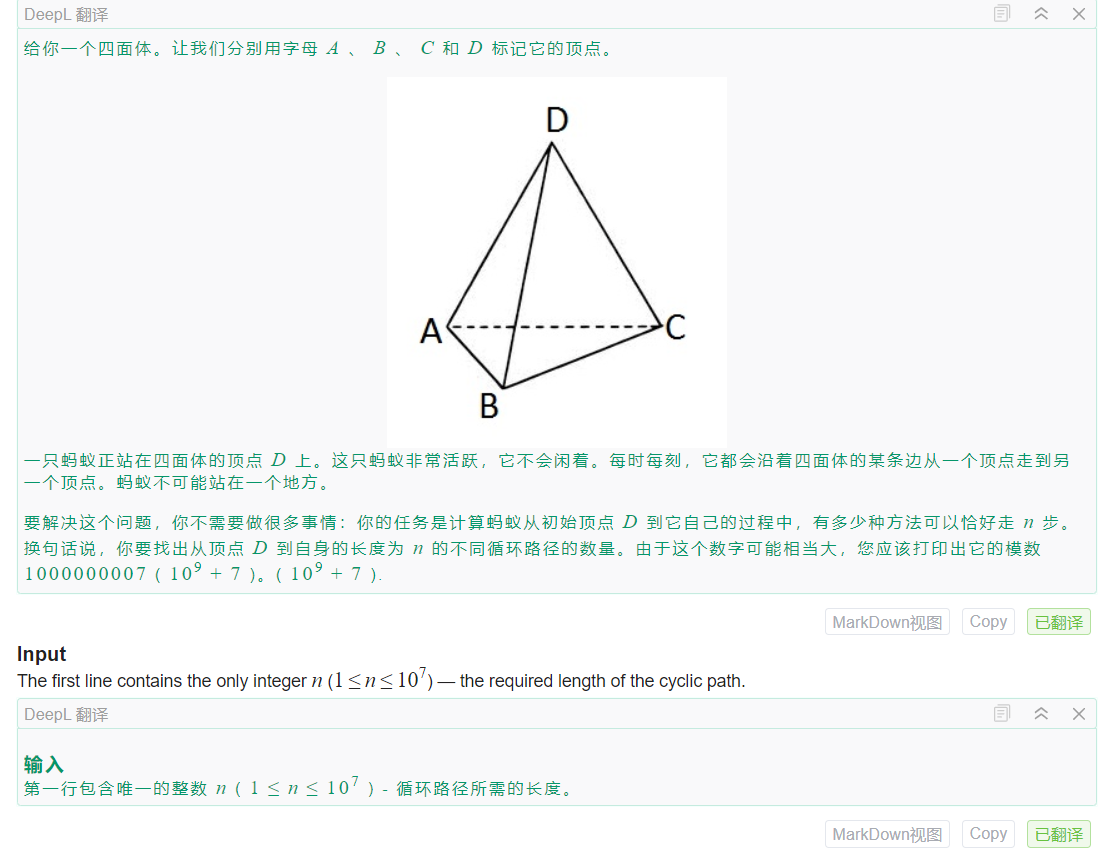
E. Tetrahedron

题意

从一个顶点出发走过路径长度为n回到出发点的方案总数

题解

考虑dp
$f[i][0|1|2|3]$:走了i步，现在在j点的方案总数
转移：
$f[i][0]=f[i-1][1]+f[i-1][2]+f[i-1][3]$
$f[i][1]=f[i-1][0]+f[i-1][2]+f[i-1][3]$
$f[i][2]=f[i-1][0]+f[i-1][1]+f[i-1][3]$
$f[i][3]=f[i-1][0]+f[i-1][1]+f[i-1][2]$

代码

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pll pair<long long, long long>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;
const int mod=1e9+7;
int dp[3][5];
void solve()
{int n;cin>>n;dp[0][0]=1;rep(i,1,n){int u=i&1,v=(i-1)&1;dp[u][0]=(dp[v][1]+dp[v][2]+dp[v][3])%mod;dp[u][1]=(dp[v][0]+dp[v][2]+dp[v][3])%mod;dp[u][2]=(dp[v][0]+dp[v][1]+dp[v][3])%mod;dp[u][3]=(dp[v][0]+dp[v][1]+dp[v][2])%mod;}cout<<dp[n&1][0]<<endl;
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}

总结

一定要开long long，容易忘直接$definelonglongint$
爆空间开滚动数组优化。