文章目录
- 基本思想:
- 步骤:
- 复杂度:
- 注意事项:
- 代码实现
- K 站中转内最便宜的航班
Dijkstra 算法是一种用于解决单源最短路径问题的经典算法。该问题的目标是找到从图中的一个固定顶点(称为源点)到图中所有其他顶点的最短路径。
以下是 Dijkstra 算法的基本思想和步骤:
基本思想:
- Dijkstra 算法通过贪心策略逐步扩展已找到的最短路径集合,直到到达目标顶点或者所有顶点都被访问过。
步骤:
-
初始化:初始化距离和父节点信息。
- 创建一个距离字典
distances,用于存储从源点到每个顶点的当前最短距离估计。 - 初始化源点到自身的距离为 0,其他顶点到源点的距离为正无穷大。
- 创建一个父节点字典
parents,用于记录最短路径上每个顶点的前一个顶点。
- 创建一个距离字典
-
构建优先队列:将所有顶点及其距离值放入优先队列中。
- 使用最小堆作为优先队列,距离作为优先级。
-
主循环:重复以下步骤直到优先队列为空:
- 从优先队列中弹出一个顶点
current_vertex,其到源点的距离current_distance是已知的最小值。 - 对于当前顶点的每个相邻顶点
neighbor:- 计算从源点经过
current_vertex到达neighbor的距离new_distance。 - 如果
new_distance小于distances[neighbor],更新distances[neighbor]和parents[neighbor]。 - 将
(new_distance, neighbor)插入优先队列,以便下一次选择。
- 计算从源点经过
- 从优先队列中弹出一个顶点
-
最终结果:当优先队列为空时,所有顶点的最短路径都已经计算完成,从源点到每个顶点的最短路径长度保存在
distances字典中,而最短路径上的父节点关系保存在parents字典中。
复杂度:
- 时间复杂度:O((V+E)logV),其中 V 是顶点数量,E 是边数量。
- 空间复杂度:O(V),存储距离和父节点的字典。
注意事项:
- Dijkstra 算法要求图中所有边的权值非负。
- 对于稀疏图,可以使用优先队列实现,而对于稠密图,则可能需要使用 Fibonacci 堆等更复杂的数据结构以获得更好的性能。
Dijkstra 算法是一种十分重要且常用的算法,在网络路由、图形可视化等领域都有广泛应用。
代码实现
import heapq # 导入 heapq 模块def dijkstra(graph, start):distances = {vertex: float('infinity') for vertex in graph} # 初始化距离字典,用于存储从起始顶点到各顶点的当前最短距离distances[start] = 0 # 起始顶点到自身的距离为0pq = [(0, start)] # 使用优先队列存储待访问的顶点while pq: # 开始遍历直到优先队列为空current_distance, current_vertex = heapq.heappop(pq) # 从优先队列中弹出当前距离最短的顶点if current_distance > distances[current_vertex]: # 如果当前顶点的距离已经被更新过,跳过continuefor neighbor, weight in graph[current_vertex].items(): # 遍历当前顶点的相邻顶点distance = current_distance + weight # 计算通过当前顶点到达相邻顶点的距离if distance < distances[neighbor]: # 如果经过当前顶点到相邻顶点的距离更短,则更新相邻顶点的距离并将其加入优先队列distances[neighbor] = distanceheapq.heappush(pq, (distance, neighbor))return distances# 示例图
graph = { # 定义示例图'A': {'B': 1, 'C': 4},'B': {'A': 1, 'C': 2, 'D': 5},'C': {'A': 4, 'B': 2, 'D': 1},'D': {'B': 5, 'C': 1}
}start_vertex = 'A' # 定义起始顶点
print("从顶点 {} 到各顶点的最短距离:".format(start_vertex)) # 打印提示信息
print(dijkstra(graph, start_vertex)) # 调用 dijkstra 函数并打印结果K 站中转内最便宜的航班

import heapq
from collections import defaultdictclass Solution:def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:# 创建一个空的字典用于存储图的邻接关系graph = defaultdict(dict)# 将航班信息填充到图中for a, b, c in flights:graph[a][b] = c# num列表表示从起点src到每个顶点的最小次数,初始值为n+1num = [n + 1] * n # 优先队列pq,用于存储当前距离、当前顶点、到达当前顶点的次数pq = [(0, src, 0)] while pq:# 从优先队列中弹出当前距离最小的顶点及其距离和到达该顶点的次数current_distance, current_vertex, current_num = heapq.heappop(pq)# 如果当前顶点就是目标终点,则返回当前距离if current_vertex == dst:return current_distance# 如果当前到达该顶点的次数超过了k,或者当前次数已经大于记录的最小次数,则继续下一次循环if current_num > k or current_num > num[current_vertex]:continue# 更新记录到达当前顶点的次数num[current_vertex] = current_num# 遍历当前顶点的所有邻居for neighbor, weight in graph[current_vertex].items():# 新的距离是到达当前顶点的距离加上当前顶点到邻居的距离distance = current_distance + weight# 新的到达该邻居的次数是当前次数加1newnum = current_num + 1# 将新的距离、邻居顶点、到达次数加入优先队列heapq.heappush(pq, (distance, neighbor, newnum))# 如果最终没有找到目标终点,则返回-1return -1
分析:- 与Dijkstra 算法的模板类似但是又有不同地方:
相同:利用优先队列进行相对应的信息的存储,其实就是实现遍历的一个过程
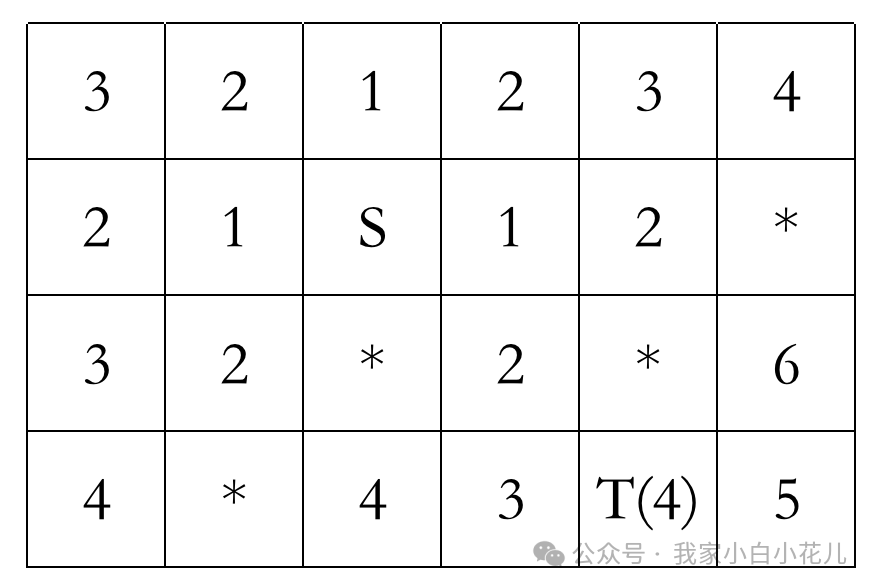
不同之处:关注于以出发点为中心的类似一个圆的一个不超过k 步的一个范围
![[1-docker-01]centos环境安装docker](https://img-blog.csdnimg.cn/direct/6dba3d59df004523973f1e7c35c5f7d5.png)







![[Doris] Doris的安装和部署 (二)](https://img-blog.csdnimg.cn/direct/ca706b5818654115af0ee6daac0a7097.png)