机器学习：卷积介绍及代码实现卷积操作

在这里插入图片描述

传统卷积运算是将卷积核以滑动窗口的方式在输入图上滑动，当前窗口内对应元素相乘然后求和得到结果，一个窗口一个结果。相乘然后求和恰好也是向量内积的计算方式，所以可以将每个窗口内的元素拉成向量，通过向量内积进行运算，多个窗口的向量放在一起就成了矩阵，每个卷积核也拉成向量，多个卷积核的向量排在一起也成了矩阵，于是，卷积运算转化成了矩阵乘法运算。下图很好地演示了矩阵乘法的运算过程：

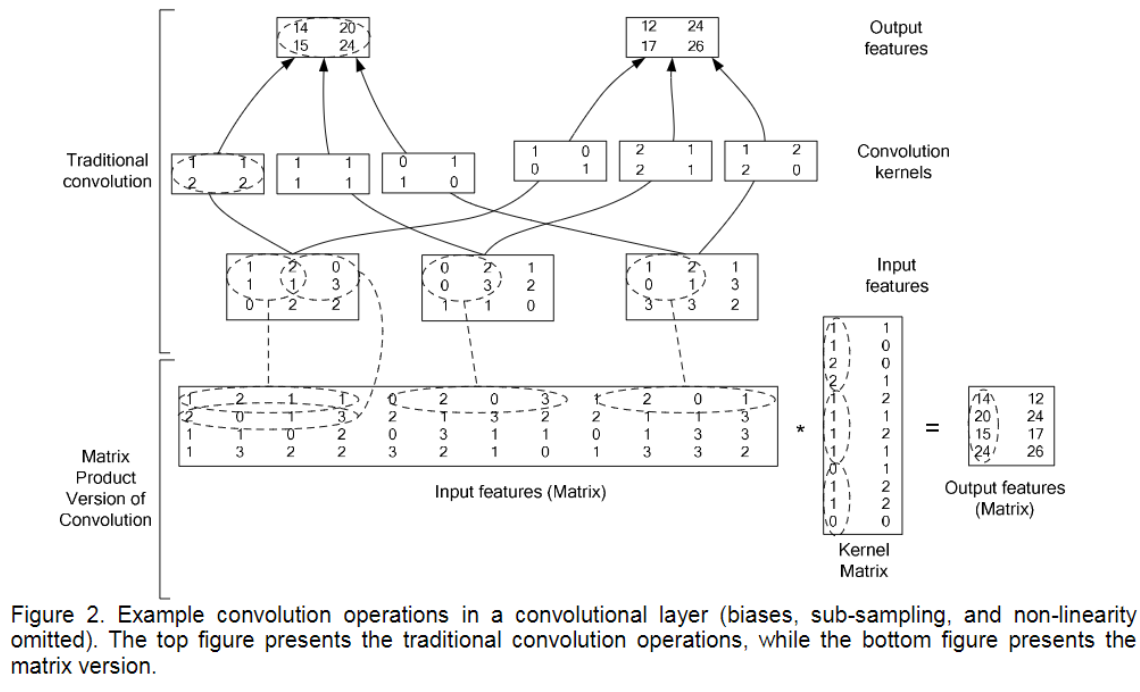
im2col

将卷积运算转化为矩阵乘法，从乘法和加法的运算次数上看，两者没什么差别，但是转化成矩阵后，运算时需要的数据被存在连续的内存上，这样访问速度大大提升（cache），同时，矩阵乘法有很多库提供了高效的实现方法，像BLAS、MKL等，转化成矩阵运算后可以通过这些库进行加速。

缺点呢？这是一种空间换时间的方法，消耗了更多的内存——转化的过程中数据被冗余存储。

代码实现

太久没写python代码，面试的时候居然想用c++来实现，其实肯定能实现，但是比起使用python复杂太多了，所以这里使用python中的numpy来实现。

一、滑动窗口版本实现（这个好理解）

import numpy as np# 为了简化运算，默认batch_size = 1
class my_conv(object):def __init__(self, input_data, weight_data, stride, padding = 'SAME'):self.input = np.asarray(input_data, np.float32)self.weights = np.asarray(weight_data, np.float32)self.stride = strideself.padding = paddingdef my_conv2d(self):"""self.input: c * h * w  # 输入的数据格式self.weights: c * h * w"""[c, h, w] = self.input.shape[kc, k, _] = self.weights.shape  # 这里默认卷积核的长宽相等assert c == kc  # 如果输入的channel与卷积核的channel不一致即报错output = []# 分通道卷积，最后再加起来for i in range(c):  f_map = self.input[i]kernel = self.weights[i]rs = self.compute_conv(f_map, kernel)if output == []:output = rselse:output += rsreturn output# padding和rs的宽高计算全部基于rs_h = (h - k + 2p)//s + 1def compute_conv(self, fm, kernel):[h, w] = fm.shape[k, _] = kernel.shapeif self.padding == 'SAME': # 知道rs_hw，求pad_hwrs_h = h // self.striders_w = w // self.stridepad_h = (self.stride * (rs_h - 1) + k - h) // 2pad_w = (self.stride * (rs_w - 1) + k - w) // 2elif self.padding == 'VALID': # 知道pad_hw，求rspad_h = 0pad_w = 0rs_h = (h - k) // self.stride + 1rs_w = (w - k) // self.stride + 1elif self.padding == 'FULL': # 知道pad_hw，求rs_hwpad_h = k - 1pad_w = k - 1rs_h = (h + 2 * pad_h - k) // self.stride + 1rs_w = (w + 2 * pad_w - k) // self.stride + 1padding_fm = np.zeros([h + 2 * pad_h, w + 2 * pad_w], np.float32)padding_fm[pad_h:pad_h+h, pad_w:pad_w+w] = fm  # 完成对fm的zeros paddingrs = np.zeros([rs_h, rs_w], np.float32)for i in range(rs_h):for j in range(rs_w):roi = padding_fm[i*self.stride:(i*self.stride + k), j*self.stride:(j*self.stride + k)]rs[i, j] = np.sum(roi * kernel) # np.asarray格式下的 * 是对应元素相乘return rsif __name__=='__main__':input_data = [[[1, 0, 1, 2, 1],[0, 2, 1, 0, 1],[1, 1, 0, 2, 0],[2, 2, 1, 1, 0],[2, 0, 1, 2, 0],],[[2, 0, 2, 1, 1],[0, 1, 0, 0, 2],[1, 0, 0, 2, 1],[1, 1, 2, 1, 0],[1, 0, 1, 1, 1],],]weight_data = [[[1, 0, 1],[-1, 1, 0],[0, -1, 0],],[[-1, 0, 1],[0, 0, 1],[1, 1, 1],]]conv = my_conv(input_data, weight_data, 1, 'SAME')print(conv.my_conv2d())

二、矩阵乘法版本实现

import numpy as np# 为了简化运算，默认batch_size = 1
class my_conv(object):def __init__(self, input_data, weight_data, stride, padding = 'SAME'):self.input = np.asarray(input_data, np.float32)self.weights = np.asarray(weight_data, np.float32)self.stride = strideself.padding = paddingdef my_conv2d(self):"""self.input: c * h * w  # 输入的数据格式self.weights: c * h * w"""[c, h, w] = self.input.shape[kc, k, _] = self.weights.shape  # 这里默认卷积核的长宽相等assert c == kc  # 如果输入的channel与卷积核的channel不一致即报错# rs_h与rs_w为最后输出的feature map的高与宽if self.padding == 'SAME':pad_h = (self.stride * (h - 1) + k - h) // 2pad_w = (self.stride * (w - 1) + k - w) // 2rs_h = hrs_w = welif self.padding == 'VALID':pad_h = 0pad_w = 0rs_h = (h - k) // self.stride + 1rs_w = (w - k) // self.stride + 1elif self.padding == 'FULL':pad_h = k - 1pad_w = k - 1rs_h = (h + 2 * pad_h - k) // self.stride + 1rs_w = (w + 2 * pad_w - k) // self.stride + 1# 对输入进行zeros padding，注意padding后依然是三维的pad_fm = np.zeros([c, h+2*pad_h, w+2*pad_w], np.float32)pad_fm[:, pad_h:pad_h+h, pad_w:pad_w+w] = self.input# 将输入和卷积核转化为矩阵相乘的规格mat_fm = np.zeros([rs_h*rs_w, kc*k*k], np.float32)mat_kernel = self.weightsmat_kernel.shape = (kc*k*k, 1) # 转化为列向量row = 0   for i in range(rs_h):for j in range(rs_w):roi = pad_fm[:, i*self.stride:(i*self.stride+k), j*self.stride:(j*self.stride+k)]mat_fm[row] = roi.flatten()  # 将roi扁平化，即变为行向量row += 1# 卷积的矩阵乘法实现rs = np.dot(mat_fm, mat_kernel).reshape(rs_h, rs_w) return rsif __name__=='__main__':input_data = [[[1, 0, 1, 2, 1],[0, 2, 1, 0, 1],[1, 1, 0, 2, 0],[2, 2, 1, 1, 0],[2, 0, 1, 2, 0],],[[2, 0, 2, 1, 1],[0, 1, 0, 0, 2],[1, 0, 0, 2, 1],[1, 1, 2, 1, 0],[1, 0, 1, 1, 1],],]weight_data = [[[1, 0, 1],[-1, 1, 0],[0, -1, 0],],[[-1, 0, 1],[0, 0, 1],[1, 1, 1],]]conv = my_conv(input_data, weight_data, 1, 'SAME')print(conv.my_conv2d())