首先，什么是最小生成树？

他就是无向图G中的所有生成树中树枝权值总和最小的。

如何求？

我们不妨采用以下的贪心策略：

Prim算法（复杂度：（n+m)logm)：

我们对于把上述的点看成两个集合，一个是确定了最小生成树的点，一个还没有确定，我们只要不断把距离已经确定的集合的最短的边添加进去即可。假如我们加的距离不是最小的，那么当我们假设未确定的点已经构成了他们点的最小生成树，那么我们此时用距离最小的去添加他们肯定更优。（我们对于那先未确定的点的集合，不管用什么边去联系他们任何一个点，都不会影响他们以后的最小生成树的形状，这也是贪心当前最优解可以推出全局最优解的保证）

来道模板题：

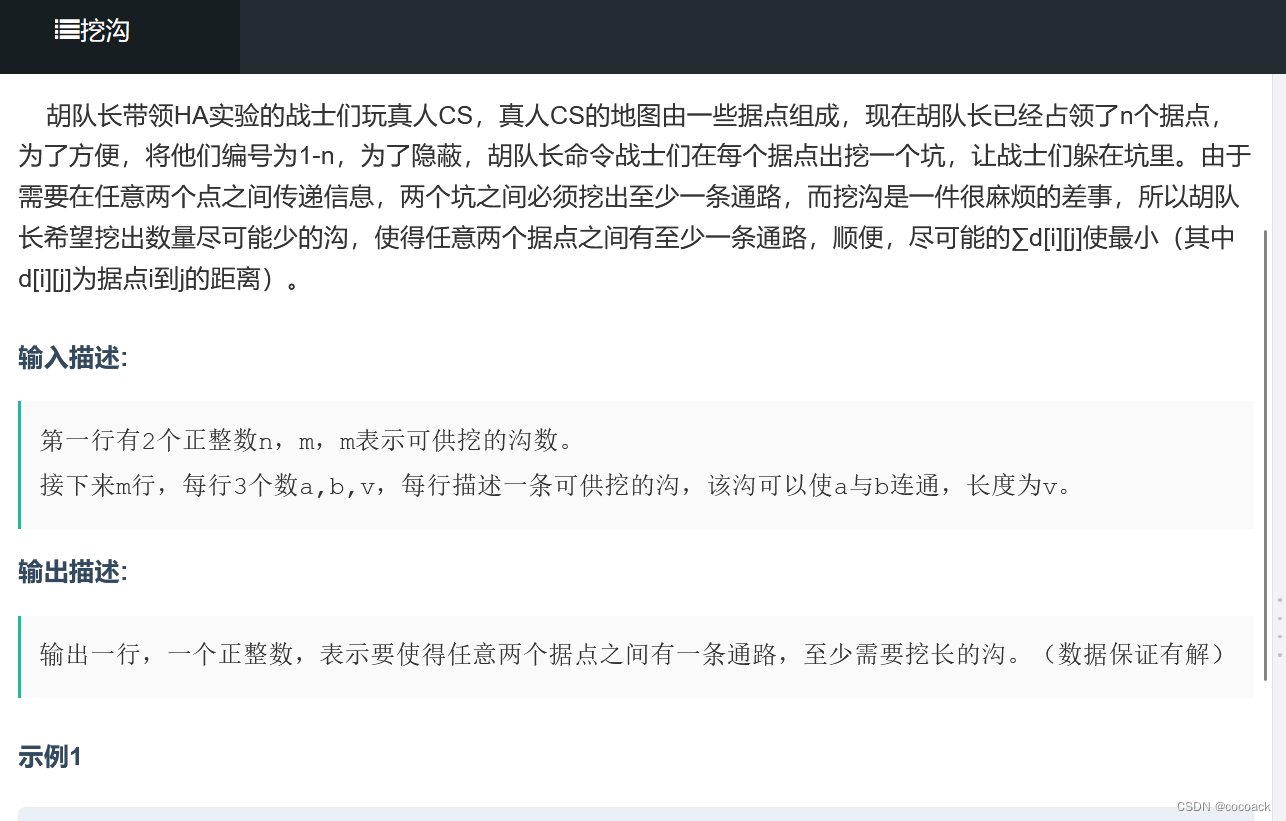
因为传递消息，至少连n-1条边，又要距离min，相当于求最小生成树，下面是AC代码（我们可以优化一下，对于还未拿出的边，若有一个比他长的则不放入队列）：

#include<bits/stdc++.h>
using namespace std;
int n,m,head[100010],a,b,v,cnt,sum;
struct node{int len,dian,next;
}edge[1000005];
void addedge(int x,int y,int v){edge[++cnt].len=v;edge[cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
int dis[100010];
struct ty{int bian,name;bool operator<(const ty &a) const{return bian>a.bian;}
};
bool vis[1000001];
priority_queue<ty> q;
int prim(){q.push({0,1});while(!q.empty()){ty ck=q.top();q.pop();if(vis[ck.name]==1) continue;vis[ck.name]=1;sum+=ck.bian;for(int i=head[ck.name];i!=-1;i=edge[i].next){if(vis[edge[i].dian]==1) continue;if(dis[edge[i].dian]<=edge[i].len) continue;dis[edge[i].dian]=edge[i].len;q.push({edge[i].len,edge[i].dian});}}return sum;
}
int main(){memset(head,-1,sizeof(head));memset(vis,0,sizeof(vis));memset(dis,0x3f,sizeof(dis));cin>>n>>m;for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&v);addedge(a,b,v);addedge(b,a,v);}cout<<prim();
}

Kruskal算法(复杂度：mlogm)：

还是采取贪心策略，只不过这次是直接选所有边下的最短边，若他们连起来还是树，就连起来，反之舍弃，用并查集维护即可。

首先，我们注意到如果每一次都可以选min的n-1条边就是最优的情况。

但是，在实际上，可能边会在同一个并查集中，说明这条边可以发挥构成树的作用，当时已经存在一点，他的作用是一样的，但是它的距离更小，因此更优。换句话说，我们就是在选n-1个在构建生成树的发挥不同作用的边，而之所以要放弃，是因为功能的重叠。

综上，这样选取的策略最优。

下面给出AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,fa[100010],a,b,v,cnt,sum;
struct node{int len,x,y;
}edge[1000005];
bool cmp(node a,node b){return a.len<b.len;
}
int find(int x){if(fa[x]==x) return x;else return fa[x]=find(fa[x]);
}
void merge(int x,int y){fa[find(x)]=find(y);
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&v);edge[++cnt].x=a;edge[cnt].y=b;edge[cnt].len=v;}sort(edge+1,edge+1+m,cmp);for(int i=1;i<=m;i++){int xx=find(edge[i].x);int yy=find(edge[i].y);if(xx==yy) continue;sum+=edge[i].len;merge(xx,yy);}cout<<sum;
}