C:Sasha and the Casino

类似于倍投法，就是在一赔一的情况下,第一次压一块钱,每输一次就押注上一次两倍的金额.

假如资金无限的话,这种方法赢的期望为无穷大.原理类似于二进制，不论你输再多次,只要赢一次总额就增加了1.比如 15 二进制1111，前3把一直输，但是只要第4把赢，就一定可以增加 1 资金.

本题大概也就是这样，假设已经输了s，那么这一把至少要投资多少才可以把之前输的全部赚回来，假设为c ,那么也就是  k*c> s+c , 变形一下就是 c>   , 这里我们下取整 再加上1 即可.

那么我们只需要判断资金是否充足即可。

void solve()
{int k, x, a;cin >> k >> x >> a;int s = 1;for (int i = 1; i <= x; i++){int t = s / (k - 1) + 1;s += t;if (s > a){cout << "NO" << endl;return;}}cout << "YES" << endl;
}

D:Sasha and a Walk in the City

 题意: 计算不存在三点在一条线上的点集的数量.反正体面是有点抽象。。

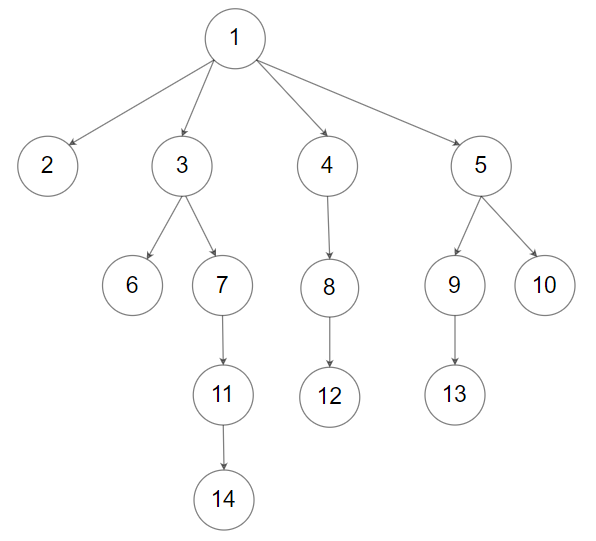
思路：我们考虑树形dp，一般先看单一的树与子树进行分析

一种是从每个叶节点到根结点形成的链上最多只有一个特殊点，用 f [ x ]保存，还有一种就是有存在两个关键点的链，用 dp[x] 保存

那么对于以 x 为根的子树，如果不选择 x 为关键点：

1.第一种情况下因为每条链上只有一个关键点，那么经过 x 的路径一定不会包含第三个关键点， x子树的所有情况可以随意组合，直接将所有子树的 f 乘起来即可

2.第二种情况下，如果 x 的一棵子树存在这样一条链，其他子树的任意节点都不能成为关键点，只能是空白一种情况，所以把所有子树dp相加

如果选择 x 成为关键点的话，子树一定不能含链，分为两种情况：

1.除了 x 均为空白，符合第一种情况,这样只有一种

2.对于一颗子树的所有不含链(也就是最多一个点）且不为空白的可能（即为 f[son]−1 ），加上 x 会构成若干条链，此时其余子树应均为空白。

两种情况相加有

   

初始化的时候，f[i]=1,叶节点为2

int f[N], dp[N];
vector<int> g[N];
void dfs(int u, int fa)
{for (auto ed : g[u]){if (ed == fa)continue;dfs(ed, u);f[u] = ((f[u] * f[ed]) % mod + mod) % mod;dp[u] = (dp[u] + dp[ed] + f[ed] - 1) % mod;}f[u]++;//对于叶节点可以使其变为2，对于其他带f[u]可以加上1f[u] %= mod;
}
void solve()
{int n;cin >> n;for (int i = 1; i <= n; i++){g[i].clear();f[i] = 1;dp[i] = 0;}for (int i = 1; i <= n - 1; i++){int a, b;cin >> a >> b;g[a].pb(b);g[b].pb(a);}dfs(1, -1);int ans = f[1] + dp[1];cout << f[1] << endl;cout << (ans % mod + mod) % mod << endl;
}