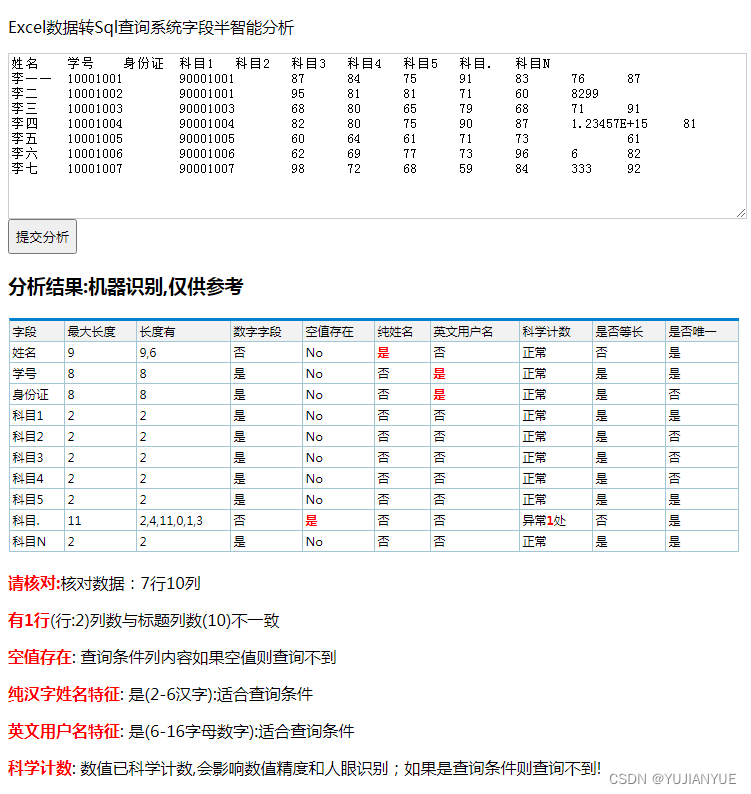
一、离散对数问题（Discrete Logarithm Problem, DLP）

问题描述：给定 有限阿贝尓群 G中的2个元素a和b，找出最小的正整数x满足：b = a ^^ x （或者证明这样的x不存在）。

二、阶数问题（Order Problem, OP）

问题描述：给定 有限阿贝尓群 G中的元素a，计算a的阶数（记号：| < a > |）。

三、根问题（Root Problem, RP）

问题描述：给定 有限阿贝尓群 G中的元素a，和整数x > 1，计算群元b，使得其满足 b ^^ x = a （或者证明群中不存在满足条件的元素）。

四、教科书描述

五、问题复杂度说明

易见，| < a > | = DLP (a, 1G), 即求阶问题和求单位元的离散对数问题等价，故有OP <= DLP。此外，若群阶已知，则群元的x次根可以高效求得，故有RP <= OP.

六、参考文献

《公钥加密和计算数论》（Public-Key Cryptography and Computational Number Theory），Edited by Kazimierz Alster, Jerzy Urbanowicz and Hugh C. Williams, de Gruyter, Berlin, Germany, 2001.