卷积操作与自定义算子开发
卷积是卷积神经网络中的基本操作,对于图像的特征提取有着关键的作用,本文首先介绍卷积的基本原理与作用,然后通过编写程序实现卷积操作,并展示了均值、高斯与sobel等几种经典卷积核的卷积效果,接着调用MindSpore中的卷积算子Conv2d来实现卷积操作,最后介绍了MindSpore中pyfunc和TBE两种自定义算子实现方法。
卷积基本原理
1.1 卷积的概念
卷积操作发展于信号处理领域,主要用于削弱原始信号中混入的噪声,典型的应用场景还有对于某个线性时不变的系统,给定输入信号和系统响应,来求系统的输出。
卷积操作引入到深度学习领域后,卷积神经网络得到了极大的发展,卷积核中的所有权重都是随机初始化,而不是一开始确定的,网络每次更新法代都是为了寻找一个最会活的卷积核权重值。
卷积与互相关有着千丝万缕的关系,对于二维卷积而言,将卷积核左右翻转、上下翻转,再将其与输入图片进行互相关运算,与直接卷积运算在输出结果上是等价的,目前各个深度学习框架的卷积层的API对于卷积运算的实现使用的是互相关运算。
1.2 卷积的计算过程
二维卷积操作相当于将卷积核作为一个滑动窗口,将其在输入张量上从左至右、从上至下地滑动,每滑动一下便将卷积核与其相应位置计算出一个加权系数,作为输出张量对应位置上的像素值,其计算过程为:将输入的张量与卷积核进行卷积操作,得到输出矩阵并将其返回。
步长为1的卷积过程如下图所示:
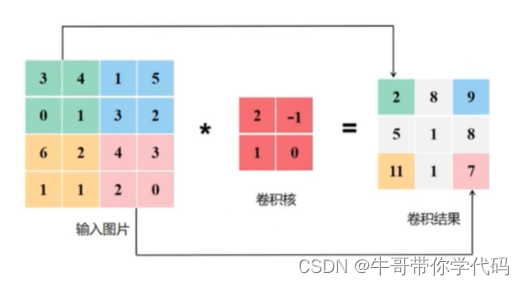
1.3 卷积的参数
卷积的参数有步长stride、填充pad、卷积核大小、深度、数量等等。其中:
- 步长表示卷积核在输入张量上每次滑动的步距,通过设置大于1的步长可以减少输出张量的大小。
- 填充表示在输入张量的周围填补行或列的多少
- 卷积核的深度与输入张量的深度相同,卷积核的数量决定了输出张量的深度
1.4 输出图片大小的计算公式
输出图片大小的计算如下:
其中:
resh、resw为输出图片的高度与宽度
datah、dataw为输入图片的高度与宽度
padh、padw为高度与宽度方向上的补边
filterh、filterw为卷积核的高度与宽度
strideh、stridew为高度与宽度方向上的步长
1.5 卷积的作用
卷积操作可以实现数据降维、特征提取等任务,通过设置不同的步长、补边与卷积核大小等参数,能够提取到图像不同的特征,完成不同的图像处理任务。
在图像处理中,卷积核也称为滤波器,如常用的均值滤波与高斯滤波能够起到图像平滑和锐化的效果,而sobel算子和Laplace算子对于图像的边缘检测有较好的效果。




![[计算机网络]---UDP协议](https://img-blog.csdnimg.cn/direct/0ae9c96e2be34572b3f51203ac4bc6bf.png)



![[word] 怎么把word表格里的字放在正中间? #职场发展#知识分享#知识分享](https://img-blog.csdnimg.cn/img_convert/f35c948dbf16018bd09033216ad272a6.jpeg)



![[Android]Frida-hook环境配置](https://img-blog.csdnimg.cn/img_convert/68d0fc3953a64c74fbc4b137b70d99d1.png)