public class Test09 {public static void main(String[] args) {//右旋 数组逆序遍历，将尾部元素，不断交换至头部int[] arr = {1,2,3,4,5,6,7,8};for(int i = arr.length-1;i>0;i--) {  //遍历一次arr[i] = arr[i] ^ arr[i-1];arr[i-1] = arr[i] ^ arr[i-1];arr[i] = arr[i] ^ arr[i-1];//int temp = arr[i];//arr[i] = arr[i-1];//arr[i-1] = temp;}System.out.println("右旋:"+Arrays.toString(arr));//左旋 数组顺序遍历，将头部元素，不断交换至尾部int[] arr1 = {1,2,3,4,5,6,7,8};for(int j = 0;j<arr1.length-1;j++) {   //遍历一次arr1[j] = arr1[j] ^ arr1[j+1];arr1[j+1] = arr1[j] ^ arr1[j+1];arr1[j] = arr1[j] ^ arr1[j+1];}System.out.println("左旋:"+Arrays.toString(arr1));}
}

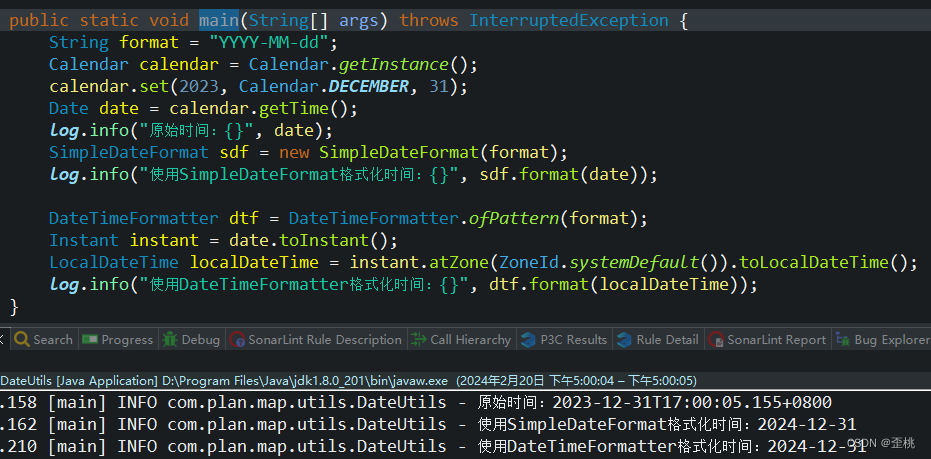
效果图：