【LeetCode】递归精选8题——基础递归、链表递归

基础递归问题：

1. 斐波那契数（简单）

1.1 递归求解

1.2 迭代求解

2. 爬楼梯（简单）

2.1 递归求解

2.2 迭代求解

3. 汉诺塔问题（简单）

3.1 递归求解

4. Pow(x, n)（中等）

4.1 递归求解

4.2 迭代求解

链表递归问题：

1. 合并两个有序链表（简单）

1.1 递归求解

1.2 迭代求解

2. 反转链表（简单）

2.1 递归求解

2.2 迭代求解

3. 两两交换链表中的节点（中等）

3.1 递归求解

3.2 迭代求解

4. 合并 K 个升序链表（困难）

4.1 递归求解

4.2 迭代求解

在解决一个规模为n的问题时，如果满足以下条件，我们可以使用递归来解决：

问题可以被划分为规模更小的子问题，并且这些子问题具有与原问题相同的解决方法。
当我们知道规模更小的子问题（规模为n-1）的解时，我们可以直接计算出规模为n的问题的解。
存在一种简单情况，或者说当问题的规模足够小时，我们可以直接求解问题。

一般的递归求解过程如下：

验证是否满足简单情况。
假设较小规模的问题已经解决，解决当前问题。

上述步骤可以通过数学归纳法来证明。

基础递归问题：

1. 斐波那契数（简单）

1.1 递归求解

重复的子问题——函数头设计

int fib(int n)

子问题在做什么——函数体设计

fib(n - 1) + fib(n - 2)

递归出口

fib(0) = 0

fib(1) = 1

class Solution {
public:int fib(int n) {if (n <= 1)return n;return fib(n - 1) + fib(n - 2);}
};

1.2 迭代求解

递归算法在计算时存在着大量的重复计算，执行效率低，n值稍大时非常耗费时间。斐波那契数列用迭代算法更高效。

class Solution {
public:int fib(int n) {if (n <= 1)return n;int a = 0;int b = 1;int c = 0;for (int i = 2; i <= n; i++){c = a + b;a = b;b = c;}return c;}
};

2. 爬楼梯（简单）

2.1 递归求解

重复的子问题——函数头设计

int climbStairs(int n)

子问题在做什么——函数体设计

如果先走1级台阶，还剩n - 1级台阶，有climbStairs(n - 1)种走法；如果先走2级台阶，还剩n - 2级台阶，有climbStairs(n - 2)种走法。一共的走法：

climbStairs(n - 1) + climbStairs(n - 2)

递归出口

当n == 1时，只有1种走法。

当n == 2时，可以一次走1级台阶，走两次；也可以一次走2级台阶，走一次。所以一共有2种走法。

climbStairs(1) = 1

climbStairs(2) = 2

class Solution {
public:int climbStairs(int n) {if (n <= 2)return n;return climbStairs(n - 1) + climbStairs(n - 2);}
};

（But这题在LeetCode上用递归会超时o(´^｀)o）

可以看出爬楼梯是斐波那契数的应用。

2.2 迭代求解

class Solution {
public:int climbStairs(int n) {if (n <= 2)return n;int a = 1;int b = 2;int c = 0;for (int i = 3; i <= n; i++){c = a + b;a = b;b = c;}return c;}
};

3. 汉诺塔问题（简单）

3.1 递归求解

重复的子问题——函数头设计

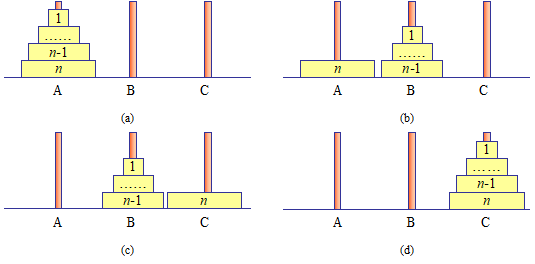
有三根柱子A、B、C，A柱上有n个盘子，将所有盘子从A柱经B柱全部移到C柱上。

void dfs(int n, vector<int>& A, vector<int>& B, vector<int>& C)

子问题在做什么——函数体设计

该问题可划分成2个自相似问题和1次移动：

将n-1个盘子从A柱经C柱全部移到B柱上：dfs(n - 1, A, C, B);
将第n个盘子从A柱移到C柱上：C.push_back(A.back()); A.pop_back();
将n-1个盘子从B柱经A柱全部移到C柱上：dfs(n - 1, B, A, C);

递归出口

当A柱只剩1个盘子时（即n == 1时），将其从A柱移到C柱上。

C.push_back(A.back());

A.pop_back();

class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {if (A.empty())return;dfs(A.size(), A, B, C);}private:// n个盘子从A经B移到Cvoid dfs(int n, vector<int>& A, vector<int>& B, vector<int>& C){if (n == 1){C.push_back(A.back());A.pop_back();return;}dfs(n - 1, A, C, B);C.push_back(A.back());A.pop_back();dfs(n - 1, B, A, C);}
};

4. Pow(x, n)（中等）

4.1 递归求解

快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。其时间复杂度为 O(log₂N)，与朴素的O(N)相比效率有了极大的提高。

$x^{n} = (x^{2})^{\frac{n}{2}}$

如果n是负数， $x^{n} = \frac{1}{x^{-n}}$ ，所以只需考虑n是自然数的情况：

假设n/2向下取整，则需要分奇偶两种情况：

当n是偶数时， $x^{n} = (x^{2})^{\frac{n}{2}}$
当n是奇数时， $x^{n} = (x^{2})^{\frac{n}{2}} * x$

重复的子问题——函数头设计

double dfs(double x, long long n) n是非负数

用long long接收n，防止-2^31转换成2^31越界。

子问题在做什么——函数体设计

判断n的奇偶性，带入不同的公式。

偶数：return dfs(x * x, n / 2); 偶数：return dfs(x * x, n / 2) * x;

递归出口

当 n == 0 时，任何数的0次幂都等于1，返回1.0

class Solution {
public:double myPow(double x, int n) {return n < 0 ? 1.0 / dfs(x, -(long long)n) : dfs(x, n);}private:double dfs(double x, long long n){if (n == 0)return 1.0;return n % 2 == 0 ? dfs(x * x, n / 2) : dfs(x * x, n / 2) * x;}
};

4.2 迭代求解

二进制角度的快速幂算法：

假设n的二进制为bk .….. b2 b1 b0，则：

$n = b_{0} * 2^{0} + b_{1} * 2^{1} + b_{2} * 2^{2} + ... + b_{k} * 2^{k}$

$x^{n} = x^{b_{0} * 2^{0} + b_{1} * 2^{1} + b_{2} * 2^{2} + ... + b_{k} * 2^{k}} = x^{2^{0} * b_{0}} * x^{2^{1} * b_{1}} * x^{2^{2} * b_{2}} * ... * x^{2^{k} * b_{k}}$

当bi == 0时， $x^{2^{i} * b_{i}} = 1$

当bi == 1时， $x^{2^{i} * b_{i}} = x^{2^{i}}$

我们从x开始不断地进行平方，如果bi == 1，就将对应的 $x^{2^{i}}$ 计入答案。

举个例子：

计算 $x^{11}$ ：ans初始值为1.0，11的二进制表示为1011，

$b_{0}=1$ ，将 $x^{1}$ 计入答案，

$b_{1}=1$ ，将 $x^{2}$ 计入答案，

$b_{2}=0$ ，将 $x^{4}$ 不计入答案，

$b_{3}=1$ ，将 $x^{8}$ 计入答案，

即 $x^{11}=x^{1}*x^{2}*x^{8}$

class Solution {
public:double myPow(double x, int n) {return n < 0 ? 1.0 / quickPower(x, -(long long)n) : quickPower(x, n);}private:double quickPower(double x, long long n){double ans = 1.0;while (n){// 如果最低位为1，将对应的x的幂值计入答案if ((n & 1) == 1){ans *= x;}x *= x;// 舍弃n的二进制的最低位，这样每次只要判断最低位即可n >>= 1;}return ans;}
};

链表递归问题：

1. 合并两个有序链表（简单）

1.1 递归求解

重复的子问题——函数头设计

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)

子问题在做什么——函数体设计

选择两个链表的头节点中值较小的那一个作为最终合并的新链表的头节点，然后将剩下的链表交给递归函数去处理。

比较list1->val和list2->val的大小（假设list1->val较小）
list1->next = mergeTwoLists(list1->next, list2);
return list1;

递归出口

当某一个链表为空的时候，返回另外一个链表。

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr)return list2;if (list2 == nullptr)return list1;if (list1->val < list2->val){list1->next = mergeTwoLists(list1->next, list2);return list1;}else{list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

1.2 迭代求解

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode* preHead = new ListNode; // 哨兵节点ListNode* tail = preHead;// 取小的尾插while (list1 && list2){if (list1->val < list2->val){tail->next = list1;tail = tail->next;list1 = list1->next;}else{tail->next = list2;tail = tail->next;list2 = list2->next;}}if (list1){tail->next = list1;}if (list2){tail->next = list2;}return preHead->next;}
};

2. 反转链表（简单）

2.1 递归求解

重复的子问题——函数头设计

ListNode* reverseList(ListNode* head)

子问题在做什么——函数体设计

将当前结点之后的链表反转，然后把当前结点添加到反转后的链表后面即可，返回反转后的头节点。

ListNode* newHead = reverseList(head->next);
head->next->next = head; head->next = nullptr;
return newHead;

递归出口

当前结点为空或者当前只有一个结点的时候，不用反转，直接返回。

class Solution {
public:ListNode* reverseList(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* newHead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newHead;}
};

2.2 迭代求解

class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* pre = nullptr;ListNode* cur = head;while (cur){ListNode* next = cur->next;cur->next = pre;pre = cur;cur = next;}return pre;}
};

3. 两两交换链表中的节点（中等）

3.1 递归求解

重复的子问题——函数头设计

ListNode* swapPairs(ListNode* head)

子问题在做什么——函数体设计

将从第三个节点开始的链表两两交换节点，然后再把前两个节点交换一下，链接上刚才处理过的链表，并返回。

ListNode* tmp = swapPairs(head->next->next);
ListNode* newHead = head->next; newHead->next = head;
head->next = tmp;
return newHead;

递归出口

当前结点为空或者当前只有一个结点的时候，不用两两交换，直接返回。

class Solution {
public:ListNode* swapPairs(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* tmp = swapPairs(head->next->next);ListNode* newHead = head->next;newHead->next = head;head->next = tmp;return newHead;}
};

3.2 迭代求解

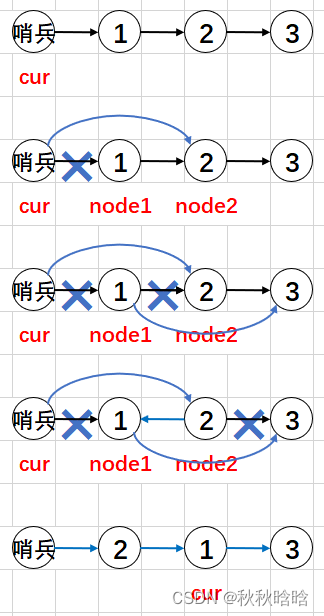
class Solution {
public:ListNode* swapPairs(ListNode* head) {ListNode* preHead = new ListNode(0, head); // 哨兵节点ListNode* cur = preHead;// cur后面的两个节点交换while (cur->next && cur->next->next){ListNode* node1 = cur->next;ListNode* node2 = cur->next->next;cur->next = node2;node1->next = node2->next;node2->next = node1;cur = node1;}return preHead->next;}
};

4. 合并 K 个升序链表（困难）

4.1 递归求解

分治的思想，类似归并排序：

划分两个子区间
分别对两个子区间的链表进行合并，形成两个有序链表
合并两个有序链表

重复的子问题——函数头设计

ListNode* merge(vector<ListNode*>& lists, int begin, int end)

子问题在做什么——函数体设计

划分两个子区间：int mid = (begin + end) / 2;
递归合并两个子区间：
ListNode* l1 = merge(lists, begin, mid);
ListNode* l2 = merge(lists, mid + 1, end);
合并两个有序链表：return mergeTowList(l1, l2);

递归出口

当区间只有一个链表时，不合并。另外，当题目给出空链表时，不合并。

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {return merge(lists, 0, lists.size() - 1);}private:ListNode* merge(vector<ListNode*>& lists, int begin, int end){if (begin > end)return nullptr;if (begin == end)return lists[begin];int mid = (begin + end) / 2;ListNode* l1 = merge(lists, begin, mid);ListNode* l2 = merge(lists, mid + 1, end);return mergeTwoLists(l1, l2);}ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){ListNode* preHead = new ListNode; // 哨兵节点ListNode* tail = preHead;// 取小的尾插while (list1 && list2){if (list1->val < list2->val){tail->next = list1;tail = tail->next;list1 = list1->next;}else{tail->next = list2;tail = tail->next;list2 = list2->next;}}if (list1){tail->next = list1;}if (list2){tail->next = list2;}return preHead->next;}
};

4.2 迭代求解

和“合并两个有序链表”类似，就是取小的尾插。怎么判断K个链表未合并的头节点中最小的那个？利用堆这个数据结构即可。把K个链表未合并的头节点放进一个小根堆，堆顶就是最小的那个。

class Solution {struct cmp{bool operator()(ListNode* n1, ListNode* n2){return n1->val > n2->val;}};public:ListNode* mergeKLists(vector<ListNode*>& lists) {// 创建小根堆priority_queue<ListNode*, vector<ListNode*>, cmp> heap;// 将所有头节点放进小根堆for (auto& l : lists){if (l){heap.push(l);}}// 合并链表ListNode* preHead = new ListNode; // 哨兵节点ListNode* tail = preHead;while (!heap.empty()){// 取堆顶节点尾插tail->next = heap.top();heap.pop();tail = tail->next;// 将刚才合并的节点的下一个节点补充进堆if (tail->next){heap.push(tail->next);}}return preHead->next;}
};